我用贝叶斯优化法(BayesianOptimisation)进行了实验。
,你有最大的 9 个可优化参数集。你说计算需要很长时间。
我试过用 10 个第一随机集优化 20 个参数集。我花了 1.5 个小时在贝叶斯优化(BayesianOptimisation)中计算这些组合,还没有考虑 NS 本身的计算时间(我用一个简单的实验数学公式代替了 NS)。
如果要优化 50 或 100 个参数,计算 1 组可能需要 24 小时。我认为用 NS 生成几十个随机组合并计算它们,然后通过准确性选出最佳组合会更快。
软件包讨论中提到了这个问题。一年前,作者写道,如果他找到了更快的计算软件包,他将会使用它,但现在 - 就像现在这样。
bigGp - 未找到示例中的 SN2011fe 数据集(显然是从网上下载的,页面不可用)。我无法尝试该示例。
laGP - 在拟合函数中使用了一些令人困惑的公式,并调用了数百次,而数百次 NS 计算在时间上是不可接受的。
kofnGA - 只能从 N 个最佳值中搜索 X 个最佳值。例如 100 个中的 10 个。也就是说,它不能优化所有 100 个集合。
遗传算法 也不合适,因为它们也会产生数百次对适应度函数的调用(NS 计算)。
一般来说,没有类似的算法,而且贝叶斯优化本身也太长了。
我用贝叶斯优化法(BayesianOptimisation)进行了实验。
,你有最大的 9 个可优化参数集。你说计算需要很长时间
我试过用 10 个首批随机集优化 20 个参数集。在贝叶斯优化中计算这些组合本身就花了我 1.5 个小时,这还不包括计算 NS 本身的时间(我在实验中用一个简单的数学公式代替了 NS)。
如果要优化 50 或 100 个参数,计算 1 组可能需要 24 小时。我认为更快的方法是生成几十个随机组合,然后用 NS 计算,再根据精确度选出最佳组合。
软件包讨论中提到了这个问题。一年前,作者写道,如果他找到了更快的计算软件包,他将会使用它,但现在 - 就像现在这样。
bigGp - 找不到示例中的 SN2011fe 数据集(显然是从网上下载的,页面不可用)。我无法尝试该示例。
laGP - 在拟合函数中使用了一些令人困惑的公式,并调用了数百次,而数百次 NS 计算在时间上是不可接受的。
kofnGA - 只能从 N 个最佳值中搜索 X 个最佳值。例如 100 个中的 10 个。也就是说,它不能优化所有 100 个集合。
遗传算法 也不合适,因为它们也会产生数百次对适应度函数的调用(NS 计算)。
一般来说,没有类似的算法,而贝叶斯优化算法本身又太长。
确实存在这样的问题。这与软件包是用纯 R 语言编写有关。但对我个人来说,使用它的好处要大于时间成本。还有一个软件包hyperopt(Python)/ 我还没有机会试用,而且它已经很老了。
但我想还是会有人用 C++ 重写这个软件包的。当然,你也可以自己做,把部分计算转移到 GPU 上,但这需要很多时间。除非我真的走投无路了。
现在,我会用我现有的。
祝你好运
我还用 GPfit 软件包本身的示例进行了实验。
下面是一个优化 1 个参数的示例,该参数描述了一条有 2 个顶点的曲线(GPfit f-ya 有更多顶点,我留下了 2 个):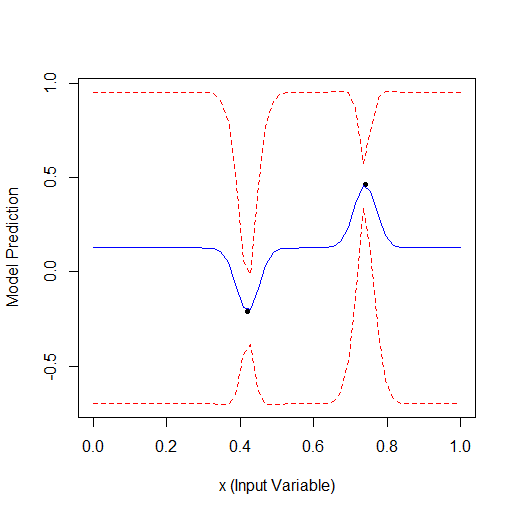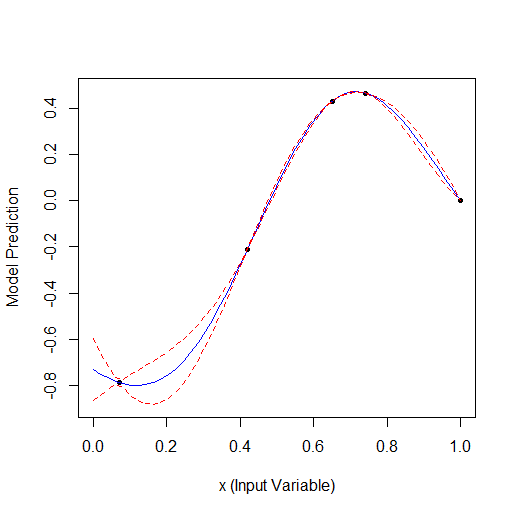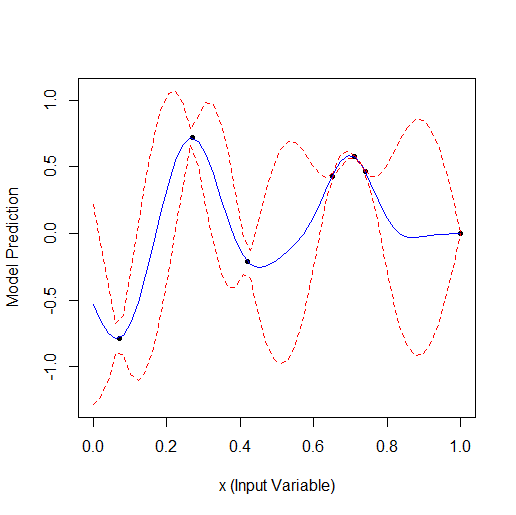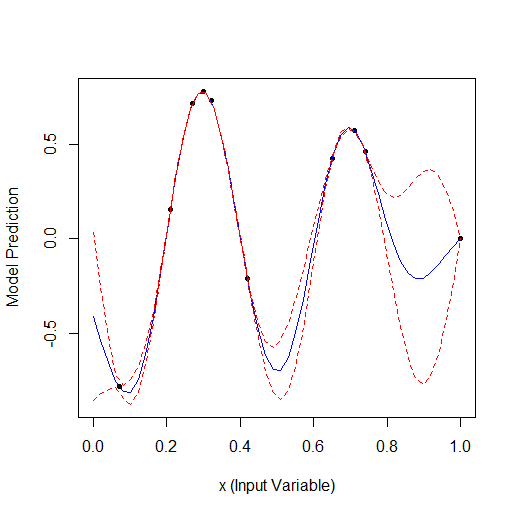
随机取 2 个点,然后进行优化。可以看到它先找到小顶点,然后找到大顶点。共有 9 次计算 - 2 次随机计算 + 7 次优化计算。
另一个 2D 示例 - 优化 2 个参数。原始的 f-y 看起来是这样的: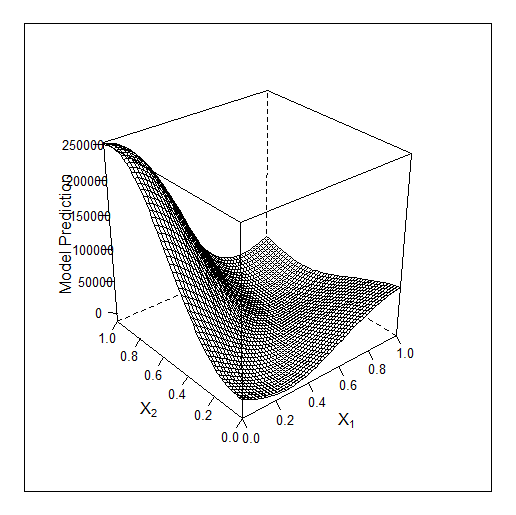
优化到 19 个点:

总计 2 个随机点 + 优化时找到的 17 个点。
比较这两个示例,我们可以发现,当增加一个参数时,找到最大值所需的迭代次数增加了一倍。
也就是说,如果优化 10 个参数,可能需要 9 * 2^10 = 9000 次计算。
虽然在 14 个计算点时,算法几乎找到了最大值,但这大约是计算次数的 1.5 倍,即 9 * 1.5:10 = 518 次计算。对于可接受的计算时间来说,这也是一个很大的数字。
文章中针对 20-30 个点得出的结果可能与真正的最大值相去甚远。
我认为,即使是这些简单的例子,遗传算法 也需要更多的点数来计算。因此,可能没有更好的选择。
我还用 GPfit 软件包本身的示例进行了试验。
以下是优化一个参数的示例,该参数描述了一条有 2 个顶点的曲线(GPfit f-ya 有更多顶点,我只留下了 2 个):
随机取 2 个点,然后进行优化。可以看到它先找到小顶点,然后找到大顶点。共有 9 次计算 - 2 次随机计算 + 7 次优化计算。
另一个 2D 示例 - 优化 2 个参数。原始的 f-ya 是这样的
优化最多 19 个点:
总计 2 个随机点 + 优化器找到的 17 个点。
比较这两个示例,我们可以发现,当增加一个参数时,找到最大值所需的迭代次数增加了一倍。
也就是说,如果优化 10 个参数,可能需要 9 * 2^10 = 9000 次计算。
虽然在 14 个计算点时,算法几乎找到了最大值,但这大约是计算次数的 1.5 倍。对于可接受的计算时间来说,这也是一个很大的数字。
1.文章中 20-30 点的结果可能与实际最大值相差甚远。
我认为,即使是这些简单的例子,遗传算法 也需要计算更多的点。所以,我想终究没有更好的选择。
好极了
很明显。
YouTube上有很多讲座解释贝叶斯优化是如何工作的。如果你还没看过,我建议你看看。信息量很大
你是如何插入动画的?
我尽可能使用贝叶斯方法。效果非常好。
1.我采用顺序优化法。首先--初始化 10 个随机点,计算 10-20 个点,接下来--初始化上次优化的 10 个最佳结果,计算 10-20 个点。通常情况下,第二次迭代后,结果不会有明显改善。
祝你好运
YouTube上发布了一些解释贝叶斯优化工作原理的讲座。如果您还没有看过,我建议您观看。内容非常丰富。
我以图片的形式查看了代码和结果(并向您展示)。最重要的是 GPfit 的高斯过程。优化是最常见的--只需使用标准 R 交付中的优化器,在 GPfit 得出的曲线/形状上寻找 2、3 等点的最大值。从上面的动画图片中可以看到 GPfit 得出的结果。优化器只是试图找出前 100 个随机点。
也许将来我有时间会去听讲座,但现在我只想把 GPfit 当成一个黑盒子。
你是如何插入动画的?
我只是逐步显示结果 GPfit::plot.GP(GP,surf_check = TRUE),然后粘贴到 Photoshop 中,并保存为 GIF 动画。
下面--初始化之前优化的10 个最佳 结果,计算 10-20 个点。
根据我的实验,最好将所有已知点都留待以后计算,因为如果删除了较低的点,GPfit 可能会认为存在有趣的点,并希望计算这些点,即会重复运行 NS 计算。而有了这些较低的点,GPfit 就会知道在这些较低的区域没有什么需要寻找的。
如果结果没有太大改善,则意味着存在一个波动较小的高原。

- 2016.04.26
- Vladimir Perervenko
- www.mql5.com
用最佳参数对模型进行前向测试
让我们来看看 DNN 的最佳参数在多长时间内能产生质量可接受的结果,以测试 "未来 "的报价值。测试将在先前优化和测试后剩余的环境中进行,具体如下。
使用 1350 条的移动窗口,训练 = 1000,测试 = 350(用于验证 - 前 250 个样本,用于测试 - 最后 100 个样本),在用于预训练的第一个(4000 + 100)条之后,以 100 步浏览数据。前进 "10 步。每一步都将训练和测试两个模型:
- 其一 - 使用预训练的 DNN,即每一步都在新的范围内进行微调;
- 第二种--在微调阶段进行优化后,在新的范围内额外训练 DNN.opt 。
#---prepare----
evalq({
step <- 1:10
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
NormData(., preproc = preproc) -> DTn
foreach(i = 1:4) %do% {
DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
} -> DTn
list(pretrain = DTn[[1]],
train = DTn[[2]],
val = DTn[[3]],
test = DTn[[4]]) -> DTn
list(
pretrain = list(
x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$pretrain$Class %>% as.data.frame()
),
train = list(
x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$train$Class %>% as.data.frame()
),
test = list(
x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$val$Class %>% as.data.frame()
),
test1 = list(
x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$test$Class %>% as.vector()
)
)
}
}, env)
使用 SRBM + upperLayer + BP 训练变体获得的预训练 DNN 和最优超参数,执行前向测试的第一部分。
#----#---SRBM + upperLayer + BP---- evalq({ #--BestParams-------------------------- best.par <- OPT_Res3$Best_Par %>% unname # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = best.par[1]; n2 = best.par[2] fact1 = best.par[3]; fact2 = best.par[4] dr1 = best.par[5]; dr2 = best.par[6] Lr.rbm = best.par[7] Lr.top = best.par[8] Lr.fine = best.par[9] Ln <- c(0, 2*n1, 2*n2, 0) foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) Res3$Dnn -> Dnn #----train/test------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnn }, env)
使用优化过程中 获得的 Dnn.opt 进行前向测试的第二阶段:
evalq({
foreach(i = step, .packages = "darch" ) %do% {
DTforv[[i]] -> X
if(i==1) {Res3$Dnn.opt -> Dnn}
#----train/test-------
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
yTest <- X$test$y[ ,1] %>% tail(100)
#numIncorrect <- sum(Ypred != yTest)
#Score <- 1 - round(numIncorrect/nrow(xTest), 2)
Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
round(3)
} -> Score3_dnnOpt
}, env)
比较测试结果,并将其放入表格中:
env$Score3_dnn env$Score3_dnnOpt
| 结果 | 得分3_dnn | 得分 3_dnnOpt |
|---|---|---|
| 准确率 精度 召回率 F1 | 准确率 精度 回收率 F1 | |
| 1 | -1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8 | -1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803 |
| 2 | -1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769 | -1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744 |
| 3 | -1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597 | -1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602 |
| 4 | -1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734 | -1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692 |
| 5 | -1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585 | -1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563 |
| 6 | -1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581 | -1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673 |
| 7 | -1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732 | -1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800 |
| 8 | -1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493 | -1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484 |
| 9 | -1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308 | -1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303 |
| 10 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
从表中可以看出,前两个步骤产生了良好的结果。两个变式的前两步质量实际上是一样的,然后就下降了。因此,可以认为,经过优化和测试后,DNN 至少能在 200-250 个小节上将分类质量保持在测试集的水平上。
你好,有什么问题?
你好,弗拉基米尔、
我不太明白为什么您的 NS 是在训练数据上训练的,而其评估是在测试数据上完成的(如果我没弄错的话,您是将其用作验证数据)。
Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3)
在这种情况下,您不会得到测试图的拟合结果吗,也就是说,您会选择在测试图上效果最好的模型吗?
我们还应该考虑到测试图非常小,有可能会拟合出一个时间规律,而这个时间规律可能很快就失效了。
也许最好在训练图上进行估计,或者在图的总和上进行估计,或者像 Darch 那样(在提交验证数据的情况下)在 Err = (ErrLeran * 0.37 + ErrValid * 0.63) 上进行估计--这些系数是默认的,但可以更改。
有很多选项,目前还不清楚哪一个是最好的。你赞成测试图的论点很有意思。
新文章 深度神经网络 (第五部分)。 DNN 超参数的贝叶斯优化已发布:
本文研究利用贝叶斯优化深度神经网络 (DNN) 超参数,获取各种训练变体的可能性。 比较不同训练变体中最优超参数 DNN 的分类品质。 DNN 最优超参数的有效性的深度已在前瞻性测试中得以验证。 改善分类品质的可能方向也已确定。
结果很好。 我们来绘制训练历史图:
plot(env$Res1$Dnn.opt, type = "class")图例 2. 由 SRBM + RP 变体训练的 DNN 历史
从图中可以看出,验证集合上的误差小于训练集合上的误差。 这意味着该模型没有过度配置,具有优良的泛化能力。 红色垂线表示模型的结果被认为是最好的,并在训练后作为结果返回。
对于其他它三种训练变体,将仅提供计算结果和历史图表,而不提供进一步的细节。 一切计算都与此类似。
作者:Vladimir Perervenko