Пакетная нормализация (Batch normalization)

В практике использования нейронных сетей используются различные подходы к нормализации данных. Все они направлены на удержание данных обучающей выборки и выходных данных скрытых слоев нейронной сети в заданном диапазоне и с определенными статистическими характеристиками выборки, такими как дисперсия и медиана. Почему же это так важно? Ведь мы помним, что в нейронах сети применяются линейные преобразования, которые в процессе обучения смещают выборку в сторону антиградиента.

Рассмотрим полносвязный перцептрон с двумя скрытыми слоями. При прямом проходе каждый слой генерирует некую совокупность данных, которые служат обучающей выборкой для последующего слоя. Результат работы выходного слоя сравнивается с эталонными данными, и на обратном проходе распространяется градиент ошибки от выходного слоя через скрытые слои к исходным данным.

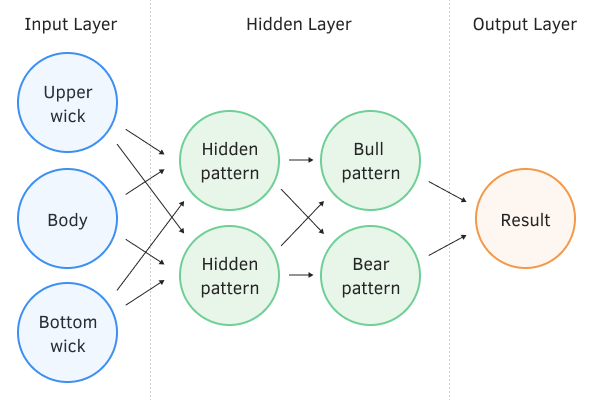
Перцептрон с двумя скрытыми слоями

Получив на каждом нейроне свой градиент ошибки, мы обновляем весовые коэффициенты, подстраивая нашу нейронную сеть под обучающие выборки последнего прямого прохода. И здесь возникает конфликт: мы подстраиваем второй скрытый слой (на рисунке выше Bull и Bear pattern) под выборку данных на выходе первого скрытого слоя (на рисунке Hidden pattern), в то время как, изменив параметры первого скрытого слоя, мы уже изменили массив данных. То есть мы подстраиваем второй скрытый слой под уже несуществующую выборку данных.

Аналогичная ситуация и с выходным слоем, который подстраивается под уже измененный выход второго скрытого слоя. А если еще учесть искажение между первым и вторым скрытыми слоями, то масштабы ошибки увеличиваются. И чем глубже нейронная сеть, тем сильнее проявление этого эффекта. Это явление было названо внутренним ковариационным сдвигом.

В классических нейронных сетях указанная проблема частично решалась уменьшением коэффициента обучения. Небольшие изменения весовых коэффициентов не сильно изменяют распределение выборки на выходе нейронного слоя. Но такой подход не решает проблемы масштабирования с ростом количества слоев нейронной сети и снижает скорость обучения. Еще одна проблема низкого коэффициента обучения — застревание в локальных минимумах (этот вопрос мы уже обсуждали в разделе о методах оптимизации нейронных сетей).

Здесь стоит еще упомянуть и о необходимости нормализации исходных данных. Довольно часто при решении различных задач на входной слой нейронной сети подаются разноплановые исходные данные, которые могут относиться к выборкам с разными распределениями. Некоторые из них могут иметь значения, по модулю значительно превышающие остальные. Такие значения будут оказывать большее влияние на конечный результат работы нейронной сети. В то же время реальное влияние описываемого фактора может быть значительно ниже, а абсолютные значения выборки обусловлены природой показателя.

На графике ниже для примера продемонстрировано отражение одного ценового движения двумя осцилляторами (MACD и RSI). При рассмотрении графиков индикаторов можно заметить корреляцию кривых. При этом числовые значения индикаторов отличаются в сотни тысяч раз. Это связано с тем, что значение индикатора RSI нормализованы по шкале от 0 до 100, а значения индикатора MACD зависят от точности указания цены на графике, поскольку MACD показывает расстояние между двумя скользящими средними.

При построении торговой стратегии мы можем пользоваться любым из этих индикаторов, а можем брать значение двух индикаторов и совершать торговые операции, только когда сигналы индикаторов совпадают. На практике такой подход позволяет отфильтровать часть ложных сигналов и тем самым снизить просадку торговой стратегии. Но прежде чем мы подадим столь различные сигналы на вход нейронной сети, желательно их привести в сопоставимый вид. Это и поможет нам сделать нормализация исходных данных.

Конечно, нормализацию исходных данных мы можем выполнить при подготовке обучающей и тестовой выборок вне нейронной сети. Но такой подход увеличивает подготовительную работу. Да и при практическом использовании такой нейронной сети нам придется все время подготавливать исходные данные по аналогичному алгоритму. Гораздо удобнее возложить эту работу на саму нейронную сеть.

В феврале 2015 года Сергей Иоффе (Sergey Ioffe) и Кристиан Сегеди (Christian Szegedy) в работе Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift предложили метод пакетной нормализации данных (Batch Normalization) для решения проблемы внутреннего ковариационного сдвига. Но этот алгоритм можно использовать и для нормализации исходных данных.

EURUSD H1

Суть метода заключалась в нормализации каждого отдельного нейрона на некоем временном интервале со смещением медианы выборки к нулю и приведением дисперсии выборки к единице.

Алгоритм проведения нормализации следующий. Вначале по выборке данных считается среднее значение.

где:

• μB — среднее арифметическое признака по выборке;
• m — размер выборки (batch).

Затем считаем дисперсию исходной выборки.

Нормализуем данные выборки, приведя выборку к нулевому среднему и единичной дисперсии.

Обратите внимание, что в знаменателе к дисперсии выборки прибавляется константа ε, небольшое положительное число с целью исключить деление на ноль.

Но как оказалось, такая нормализация может исказить влияние исходных данных. Поэтому авторы метода добавили еще один шаг — масштабирование и смещение. Были введены переменные γ и β, которые обучаются вместе с нейронной сетью методом градиентного спуска.

Применение данного метода позволяет на каждом шаге обучения получать выборку данных с одинаковым распределением, что на практике делает обучение нейронной сети более стабильным и позволяет увеличить коэффициент обучения. В целом это позволит повысить качество обучения при меньших затратах времени на обучение нейронной сети.

Но в то же время возрастают затраты на хранение дополнительных коэффициентов. Кроме того, для расчета скользящей средней и дисперсии требуется хранение в памяти исторических данных каждого нейрона на весь размер пакета. И тут можно посмотреть в сторону экспоненциальной средней: для расчета EMA достаточно предыдущего значения функции и текущего элемента последовательности.

Эксперименты, проведенные авторами метода, показывают, что применение метода Batch Normalization выступает и в роли регуляризатора. Это позволяет отказаться от использования других методов регуляризации, в частности от рассмотренного ранее Dropout. Более того, есть более поздние работы, в которых показано, что совместное использование Dropout и Batch Normalization отрицательно сказывается на результатах обучения нейронной сети.

В современных архитектурах нейронных сетей предложенный алгоритм нормализации можно встретить в различных вариациях. Авторы предлагают использовать Batch Normalization непосредственно перед нелинейностью (функцией активации). Как одну из вариаций данного алгоритма можно рассматривать метод Layer Normalization, предложенный Джимми Ли Ва (Jimmy Lei Ba), Джами Райн Кирос (Jamie Ryan Kiros) и Джефри Хинтон (Geoffrey E. Hinton) в июле 2016 года в работе Layer Normalization.