Возникла потребность интерполировать ф-ю с произвольными настройками, выбрал сплайны
Правильно понимаю, что за счет кол-ва узловых точек буду получать различные интерполянты, что еще можно варьировать?
И второй вопрос, что лучше выбрать для интерполяции из списка если мне нужно просто строить много различных интерполяций исходного ряда (вариативность важна)
Что лучше выбрать - очень непростой вопрос. Один из подходов, называемый минимизацией эмпирического риска, развит в книге Вапник "Алгоритмы и программы восстановления зависимостей". Кажется, 1972.
Что лучше выбрать - очень непростой вопрос. Один из подходов, называемый минимизацией эмпирического риска, развит в книге Вапник "Алгоритмы и программы восстановления зависимостей". Кажется, 1972.
максимизация правдоподобия\минимизация эмпирического риска, как понимаю, это просто общее название для соответствующих алгоритмов. Мне сам алгоритм не нужен, нужно просто модифить кривульки желательно быстро и вариативно, с возможностью находить значения интерполянта на новых точках (пакет сплайнов позволяет последнее)
максимизация правдоподобия\минимизация эмпирического риска, как понимаю, это просто общее название для соответствующих алгоритмов. Мне сам алгоритм не нужен, нужно просто модифить кривульки желательно быстро и вариативно, с возможностью находить значения интерполянта на новых точках (пакет сплайнов позволяет последнее)
И метод максимального правдоподобия, и минимизации (вспомнил, не эмпирического, а среднего) риска - названия не алгоритмов, а способов целеполагания при постановке задач. Если цель достижима, она порождает какой-нибудь алгоритм, который обязательно соответствует цели, является реализацией ее достижения в конкретных случаях. Если Вам не нужны ни цели, ни алгоритмы их достижения, то для задачи выбора интерполирующих функций никаких рекомендаций дать нельзя. Остается выбирать, как сердце подсказывает...
Возникла потребность интерполировать ф-ю с произвольными настройками, выбрал сплайны
Правильно понимаю, что за счет кол-ва узловых точек буду получать различные интерполянты, что еще можно варьировать?
И второй вопрос, что лучше выбрать для интерполяции из списка если мне нужно просто строить много различных интерполяций исходного ряда (вариативность важна)
Для трейдера самым ценным является не интерполяция и не аппроксимация, а экстраполяция.
Для экстраполяции сплайны непригодны.
Имею большой опыт и понимание в полиномиальной аппроксимации-экстраполяции. Поменьше опыта- Фурье.
Экстраполяции методами полинома и Фурье имеют абсолютно разную природу. Экстраполяция по Фурье может быть применима только на флэтовом рынке ввиду своей периодической природы (эта линия - сумма синусоид различной частоты, фазы и амплитуды) и она все время наровит вернуться обратно. Тогда как полиномиальная экстраполяция, наоборот, хороша при тренде, т.к. пытается все время "улететь" вниз или вверх ввиду своей степенной природы.
Поэтому есть целесообразность объединять эти два метода для хороших результатов в экстраполяции.
Особый интерес для программистов представляет именно полиномиальная аппроксимация по причине того, что этот вид аппроксимации очень хорошо поддается оптимизации и возможностью очень быстрого расчета. Мне удалось выйти из циклов для расчета коэффициентов.
Так же необходимо не забывать, что все виды аппроксимации создают перерисовываемые линии с каждой новой точкой. Неперерисовываемым является лишь трассер от аппроксимирующей линии.
Полиномиальная аппроксимации имеет только одно решение в отличии от Фурье. Это позволяет создавать уникальные неперерисовываемые скользящие:
Понятно, наугад это тоже неплохо. Значит никто аналогичные задачи не решал. Визуализирую, посмотрю.
Никто не решал - неверно. Все способы интерполяции имеют свое теоретическое обоснование и, как правило, ясную цель. Например, кубические сплайны дефекта два минимизируют потенциальную энергию упругого изгиба линейки, проходящей через гвоздики, вбитые в доску в узлах сплайна. Таким способом из таблицы точек получали гладкую (дефект меньше 3) кривую на чертеже с обводами судна или с профилем крыла. Эти же сплайны изображают прогиб многоопорной балки в сопромате. Очень часто цель - минимизация суммы отклонений координат в интерполяционных узлах.Чтобы сравнить между собой итоги интерполяции с разным целями, нужна обобщающая цель, критерий, который вычислим для любого метода интерполяции. Он стоится на основе учета числа определяемых коэффициентов. Грубо говоря, если полиномиальная аппроксимация при росте степени полинома от 3 до 7 снижает сумму квадратов отклонений на 20%, то степень 3 выбрать разумнее, чем 7. Аналог в радиотехнике, если не путаю - частота среза фильтра.
Для трейдера самым ценным является не интерполяция и не аппроксимация, а экстраполяция.
Для экстраполяции сплайны непригодны.
Имею большой опыт и понимание в полиномиальной аппроксимации-экстраполяции. Поменьше опыта- Фурье.
Экстраполяции методами полинома и Фурье имеют абсолютно разную природу. Экстраполяция по Фурье может быть применима только на флэтовом рынке ввиду своей периодической природы (эта линия - сумма синусоид различной частоты, фазы и амплитуды) и она все время наровит вернуться обратно. Тогда как полиномиальная экстраполяция, наоборот, хороша при тренде, т.к. пытается все время "улететь" вниз или вверх ввиду своей степенной природы.
Поэтому есть целесообразность объединять эти два метода для хороших результатов в экстраполяции.
Особый интерес для программистов представляет именно полиномиальная аппроксимация по причине того, что этот вид аппроксимации очень хорошо поддается оптимизации и возможностью очень быстрого расчета. Мне удалось выйти из циклов для расчета коэффициентов.
Так же необходимо не забывать, что все виды аппроксимации создают перерисовываемые линии с каждой новой точкой. Неперерисовываемым является лишь трассер от аппроксимирующей линии.
Полиномиальная аппроксимации имеет только одно решение в отличии от Фурье. Это позволяет создавать уникальные неперерисовываемые скользящие:
Нормально. Экстраполировать мне нечего, нужна именно интерполяция. В том плане что прогноз по такой экстраполяции бессмысленно потом делать. Надо что бы Линию эту как можно более сильно кумарило из стороны в сторону, как вашу синюю. И что бы можно было получить решение на новых точках, да (без пересчета заново, по уже имеющейся формуле).
Вот просто и спросил что лучше использовать - полиномы или сплайны или какие-то подвиды. И может быть и 10-й степени тоже было бы прикольно.
Никто не решал - неверно. Все способы интерполяции имеют свое теоретическое обоснование и, как правило, ясную цель. Например, кубические сплайны дефекта два минимизируют потенциальную энергию упругого изгиба линейки, проходящей через гвоздики, вбитые в доску в узлах сплайна. Таким способом из таблицы точек получали гладкую (дефект меньше 3) кривую на чертеже с обводами судна или с профилем крыла. Эти же сплайны изображают прогиб многоопорной балки в сопромате. Очень часто цель - минимизация суммы отклонений координат в интерполяционных узлах.Чтобы сравнить между собой итоги интерполяции с разным целями, нужна обобщающая цель, критерий, который вычислим для любого метода интерполяции. Он стоится на основе учета числа определяемых коэффициентов. Грубо говоря, если полиномиальная аппроксимация при росте степени полинома от 3 до 7 снижает сумму квадратов отклонений на 20%, то степень 3 выбрать разумнее, чем 7. Аналог в радиотехнике, если не путаю - частота среза фильтра.
Просто если я начну пытаться объяснять все что я с этим собираюсь делать то это опять переживаний на несколько страниц :) Нужна вариативность, разные степени полиномов, кол-во точек сетки и т.п.
Нормально. Экстраполировать мне нечего, нужна именно интерполяция. В том плане что прогноз по такой экстраполяции бессмысленно потом делать. Надо что бы Линию эту как можно более сильно кумарило из стороны в сторону, как вашу синюю. И что бы можно было получить решение на новых точках, да (без пересчета заново, по уже имеющейся формуле).
Вот просто и спросил что лучше использовать - полиномы или сплайны или какие-то подвиды. И может быть и 10-й степени тоже было бы прикольно.
Именно интерполяция? Уверены? Не аппроксимация? И причем неперерисовываемая?
Вы же не будете интерполировать каждый тик.
Если Вам нужна интерполяция по промежуточным узлам (узлы ZigZag например) без перерисовки, то весь смысл заключается где будет следующий узел.
Создать неперерисовываемый четкий ZigZag можно только в одном случае - если у вас есть машина времени. Вы ни как не сможете определить без машины времени, что текущий бар - это экстремум.
На форуме периодически возникают кто-нибудь, которых я называю "дорисовывателями хвостиков".
Весь смысл в этом хвостике.
Классика этого жанра - сдвинуть SMA влево на полпериода, и , как бы невзначай, эти полпериода дорисовать полиномом какой-то степени. Вот например - https://www.mql5.com/ru/forum/224374. Наверняка это уже видели.
Можно сделать очень красивую интерполяцию по экстремумам зигзага с помощью сплайнов, но нужно четко понимать, что между последними двумя или тремя узлами будет перерисовка. Без нее ну никак!
Если без перерисовки то это уже не интерполяция, а то что я называю трассирующим следом от аппроксимирующей линии ( не интерполяционной!).
Кроме полиномов пока ничего не вижу вразумительного.
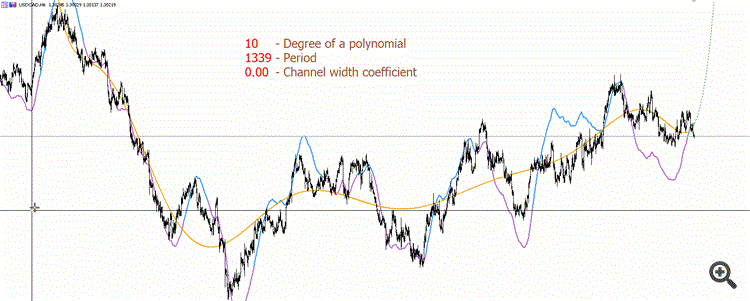
Вот специально записал гифку для демонстрации примера полинома более высокой степени (10), чтобы было понимание, насколько это менее "красиво" чем хотелось бы :))
Фиолетово-синяя линия неперерисовываемая. Фиолетовый цвет - полином "смотрит вниз", синий - полином "смотрит вверх".
Причем для вычисления полиномов высоких степеней точности double не хватает. Нужно будет использовать специальные библиотеки с применение типов более высокой точности. То, что "трассер" начинает "прыгать" на малых периодах на гифке - это причина именно не хватки точности double.
Но лично я пока не вижу практического применения полиномов степени более 5.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Возникла потребность интерполировать ф-ю с произвольными настройками, выбрал сплайны
Правильно понимаю, что за счет кол-ва узловых точек буду получать различные интерполянты, что еще можно варьировать?
И второй вопрос, что лучше выбрать для интерполяции из списка если мне нужно просто строить много различных интерполяций исходного ряда (вариативность важна)