Я как будто оказался в перевернутом мире и код теперь исполняется не сверху вниз, а снизу вверх:
void OnStart()
{
double close[]; //Объявляем динамический массив цен закрытия
int copied=CopyClose(symbol,timeframe,0,1001,close); //копируем цены закрытия выбранной пары в
//массив close[]
ArrayResize(close,1001); //образмериваем массив
ArraySetAsSeries(close,true);
if(bars<1001) //создаем условие наличия 1001 бара истории
{
Comment("Too few bars are available! Try another timeframe.");
Sleep(10000); //задержка надписи в течение 10 секунд
Comment("");
return;
}
...
Вау, только начнешь какую-то тему долбить и тут тебе на статья по ней.. круто, спасибо :)
Но, это маленько неверный путь, неверное понимание сути прогнозирования по фракталам, один херст вообще ничего не даст, все намного сложнее.
А вторая часть вообще реклама.. ну как же так :(
Очень интересно. Спасибо автору. А можно было бы показать пример нетолько исследования в прошлом, но и последующего применения. Установив взаимосвязь на прошлых данных, нужно понять как живет она в дальнейшем.
Вау, только начнешь какую-то тему долбить и тут тебе на статья по ней.. круто, спасибо :)
Но, это маленько неверный путь, неверное понимание сути прогнозирования по фракталам, один херст вообще ничего не даст, все намного сложнее.
А вторая часть вообще реклама.. ну как же так :(
Максим, спасибо за комментарий!
Да, Вы правы, конечно же вычисление коэффициента Херста - это лишь база для того, чтобы получить хотя бы малейшее представление о применение своего рода мат статистики в изучении временных рядов. Поддерживаю Ваше замечание и также считаю, что применять только лишь анализ коэффициента для прогнозирования динамики рынка было бы наивным и неверным решением. Разумеется, нужно строить стратегию на основе совокупных показателей и применяя различные индикаторы и источники.
В следующей статье обязательно продемонстрирую Вам свое правильное понимание фрактального анализа.
Еще раз спасибо за комментарий.
P.S. Предложили сделать ревью на имеющиеся в MT5 инструменты подобного анализа. Воспользовался возможностью прорекламировать.
А реклама лично меня не смущает. Куда нынче без нее. Она везде сейчас. Кто мешает ставить внутренние фильтры.
Крайне слабая статья, которая могла бы претендовать на курсовую работу лет 30 назад.
Если почитать, статью, то совершенно остается за кадром современное состояние дел, связанное с Херстом.
Автор почему-то считает, что этот коэффициент можно оценивать по МНК, а что других методов оценки в этом случае не существует.
Например, пакет FGN с функция HurstK(z), в которой производится непараметрическая оценка коэффициента Херста, которая дает гораздо более точную величину.
Если бы автор потрудился сделать обзор литературы в этой области, то он не прошел бы мимо классической работы, в которой в частности вводится понятие дробных ARIMA, что позволяет рассматривать показатель Херста не только как таковой, а в рамках соответствующих моделей, более того автор бы увидел, что существуют в R пакеты, которые обобщили коэффициент Херста.
Коэффициент Херста вне рамок моделей представляет слабый интерес и идеи Херста развивались в рамках дробно-дифференцированных моделей - Fractionally differenced ARIMA aka ARFIMA(p,d,q) models
Пакет fracdiff предоставляет достаточно полный набор инструментов в этой области.
И это далеко не все в области, связанной с коэффициентом Херста.
В очередной раз констатирую, что любые статьи в области обработки временных рядов без соответствующего обзора средств, имеющихся в рамках R, выглядят крайне невежественными с отставанием на несколько десятков лет
Крайне слабая статья, которая могла бы претендовать на курсовую работу лет 30 назад.
Если почитать, статью, то совершенно остается за кадром современное состояние дел, связанное с Херстом.
Автор почему-то считает, что этот коэффициент можно оценивать по МНК, а что других методов оценки в этом случае не существует.
Например, пакет FGN с функция HurstK(z), в которой производится непараметрическая оценка коэффициента Херста, которая дает гораздо более точную величину.
Если бы автор потрудился сделать обзор литературы в этой области, то он не прошел бы мимо классической работы, в которой в частности вводится понятие дробных ARIMA, что позволяет рассматривать показатель Херста не только как таковой, а в рамках соответствующих моделей, более того автор бы увидел, что существуют в R пакеты, которые обобщили коэффициент Херста.
Коэффициент Херста вне рамок моделей представляет слабый интерес и идеи Херста развивались в рамках дробно-дифференцированных моделей - Fractionally differenced ARIMA aka ARFIMA(p,d,q) models
Пакет fracdiff предоставляет достаточно полный набор инструментов в этой области.
И это далеко не все в области, связанной с коэффициентом Херста.
В очередной раз констатирую, что любые статьи в области обработки временных рядов без соответствующего обзора средств, имеющихся в рамках R, выглядят крайне невежественными с отставанием на несколько десятков лет
Да ладно... Сана Саныч... Единственная работа за 15 лет, хоть как-то раскрывающая расчет показателя Херста. Как бы все ни было написано, есть код, по коду можно разобраться.
В отличие от вас, Сан Саныч, автор статьи умеет рассчитать показатель Херста. А вы? А вы можете только по фене ботать писать какие-то обрывки из R. Но с видом такого знатока. Как-то сильно надоело видеть ваши комментарии везде, может вам как-то стоит изменить подход к делу?.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Опубликована статья Вычисление коэффициента Херста:
В статье подробно изложен смысл показателя Херста, интерпретация его значений, алгоритм вычисления. Приведены результаты анализа некоторых сегментов финансовых рынков и представлен метод работы с программными продуктами MetaTrader 5, реализующими идею фрактального анализа.
Фрактал — математическое множество, обладающее свойством самоподобия. Иными словами, это объект, в точности или приближённо совпадающий с частью себя самого — то есть, целое имеет ту же форму, что и одна или более частей. Самый показательный пример фрактальной структуры — «фрактальное дерево»:
Ключевой параметр фрактального анализа — показатель Херста. Это мера, которую используют при анализе временных рядов.
Основой статистической модели Херста стала работа Альберта Эйнштейна о броуновском движении, которая по существу является моделью случайных блужданий частицы. Сущность теории в том, что расстояние, которое проходит частица, R, увеличивается пропорционально квадратному корню из времени T:
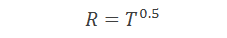
Перефразируем формулу: размах вариации, R, при большом количестве испытаний равен корню из количества испытаний, T.Автор: Dmitriy Piskarev