
Глубокая нейросеть со Stacked RBM. Самообучение, самоконтроль
Эта статья — продолжение предыдущих статей по глубоким нейросетям и выбору предикторов. В ней мы рассмотрим особенность нейросети, инициируемой Stacked RBM, а также её реализации в пакете "darch". Также будет показана возможность использования скрытых Марковских моделей для улучшения результатов предсказания нейросети. В заключение мы программно реализуем рабочий экземпляр эксперта.
Содержание
- 1. Структурная схема DBN
- 2. Подготовка и выбор данных
- 2.1. Входные переменные
- 2.2. Выходные переменные
- 2.3. Исходный датафрейм
- 2.3.1. Удаление высококоррелированных переменных
- 2.4. Выбор наиболее важных переменных
- 3. Экспериментальная часть.
- 3.1. Построение моделей
- 3.1.1. Краткое описание пакета "darch"
- 3.1.2. Построение модели DBN. Параметры.
- 3.2. Формирование обучающей и тестовой выборок.
- 3.2.1. Балансировка классов и препроцессинг.
- 3.2.2. Кодирование целевой переменной
- 3.3. Обучение модели
- 3.3.1. Претренинг
- 3.3.2. Тонкое обучение
- 3.4. Тестирование модели. Метрики.
- 3.4.1. Декодирование предсказания.
- 3.4.2. Улучшение результата предсказания
- Калибровка
- Сглаживание с помощью модели Марковской цепи
- Корректировка предсказанных сигналов по кривой теоретического баланса
- 3.4.3. Метрики
- 4. Структурная схема эксперта
- 4.1. Описание работы эксперта
- 4.2. Самоконтроль. Самообучение
- Порядок установки и запуска
- Пути и методы улучшения качественных показателей.
- Заключение
Введение
При подготовке данных для проведения экспериментов мы будем использовать переменные из предыдущей статьи об оценке и выборе предикторов. Сформируем исходный набор, проведем его очистку и выбор важных переменных.
Рассмотрим варианты разделения исходной выборки на тренировочный, тестовый и валидационный наборы.
С помощью пакета "darch" построим модель сети DBN, обучим её на наших наборах данных. После тестирования модели получим метрики, по которым сможем оценить качество модели. Рассмотрим широкие возможности, которые предоставляет пакет для настройки параметров нейросети.
Рассмотрим, чем нам могут помочь скрытые Марковские модели для улучшения предсказаний нейросети.
Разработаем эксперт, в котором модель будет обучаться периодически на лету, без прерывания торговли, по результатам постоянного контроля. В эксперте будем использовать модель DBN из пакета "darch". Приведем также вариант эксперта, построенного с использованием SAE DBN из предыдущей статьи.
Укажем пути и методы улучшения качественных показателей модели.
1. Структурная схема глубокой нейросети, инициализируемой Stacked RBM (DN_SRBM)
Напомню, DN_SRBM состоит из n-го количества RBM, равного количеству скрытых слоев нейросети, и, собственно, самой нейросети. Обучение проводится в два этапа.
Первый этап — ПРЕТРЕНИНГ. На нем каждая RBM последовательно обучается без учителя на входном наборе (без целевой). После этого веса скрытых слоев RBM переносятся в соответствующие скрытые слои нейросети.
Второй этап — ТОНКАЯ НАСТРОЙКА, на нем нейросеть обучается с учителем. Детально это рассматривалось в предыдущей статье, повторяться не будем. Укажу только, что, в отличие от пакета "deepnet", который мы использовали в предыдущей статье, пакет "darch" дает нам возможность реализовать более широкие возможности при построении и настройке модели. Подробней поговорим об этом при создании модели. На рис.1 представлена структурная схема DN_SRBM и процесс её обучения
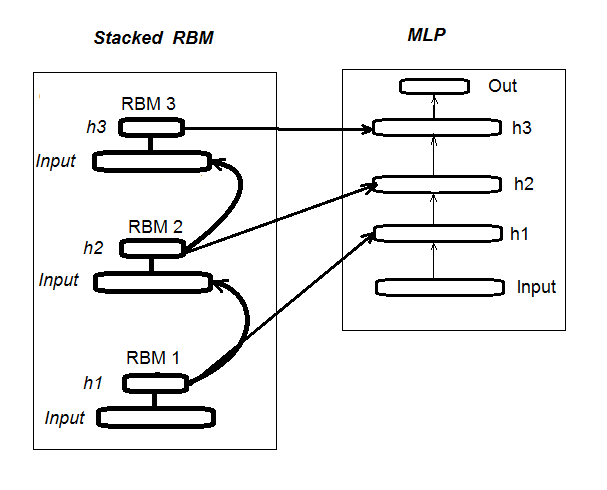
Рис. 1. Структурная схема DN SRBM
2. Подготовка и выбор данных
2.1. Входные переменные (признаки, предикторы)
В предыдущей статье мы уже рассмотрели оценку и выбор предикторов, поэтому здесь не будем детализировать этот процесс. Напомню лишь, что мы взяли 11 индикаторов (все они — осцилляторы: ADX, aroon, ATR, CCI, chaikinVolatility, CMO, MACD, RSI, stoch, SMI, volatility). Из некоторых индикаторов было выбрано по несколько переменных. Таким образом мы сформировали входной набор из 17 переменных. Возьмем котировки из последних 6000 баров на EURUSD, М30 по состоянию на 14.02.16 и вычислим значения индикаторов с помощью функции In().
#---2--------------------------------------------- In <- function(p = 16){ require(TTR) require(dplyr) require(magrittr) adx <- ADX(price, n = p) %>% as.data.frame %>% mutate(.,oscDX = DIp - DIn) %>% transmute(.,DX, ADX, oscDX) %>% as.matrix() ar <- aroon(price[ ,c('High', 'Low')], n = p) %>% extract(,3) atr <- ATR(price, n = p, maType = "EMA") %>% extract(,1:2) cci <- CCI(price[ ,2:4], n = p) chv <- chaikinVolatility(price[ ,2:4], n = p) cmo <- CMO(price[ ,'Med'], n = p) macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% as.data.frame() %>% mutate(., vsig = signal %>% diff %>% c(NA,.) %>% multiply_by(10)) %>% transmute(., sign = signal, vsig) %>% as.matrix() rsi <- RSI(price[ ,'Med'], n = p) stoh <- stoch(price[ ,2:4], nFastK = p, nFastD =3, nSlowD = 3, maType = "EMA") %>% as.data.frame() %>% mutate(., oscK = fastK - fastD) %>% transmute(.,slowD, oscK) %>% as.matrix() smi <- SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9) kst <- KST(price[ ,4])%>% as.data.frame() %>% mutate(., oscKST = kst - signal) %>% select(.,oscKST) %>% as.matrix() In <- cbind(adx, ar, atr, cci, chv, cmo, macd, rsi, stoh, smi, kst) return(In) }
На выходе получаем матрицу входных данных.
2.2 Выходные данные (целевая переменная)
В качестве целевой переменной берем сигналы, полученные с ZZ. Функция, вычисляющая зигзаг, и сигнал:
#----3------------------------------------------------ ZZ <- function(pr = price, ch = ch , mode="m") { require(TTR) require(magrittr) if (ch > 1) ch <- ch/(10 ^ (Dig - 1)) if (mode == "m") {pr <- pr[ ,'Med']} if (mode == "hl") {pr <- pr[ ,c("High", "Low")]} if (mode == "cl") {pr <- pr[ ,c("Close")]} zz <- ZigZag(pr, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) dz <- zz %>% diff %>% c(., NA) sig <- sign(dz) for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]} return(cbind(zz, sig)) }
В параметрах функции:
pr = price – матрица котировок OHLCMed;
ch – минимальная длина колена зигзага в пунктах (4 знака) или в реальных величинах (например ch = 0.0035);
mode – применяемая цена ( "m" - средняя, "hl" - High и Low. "cl" - Close), по умолчанию применяем среднюю.
Функция возвращает матрицу с двумя переменными — собственно, зигзаг и сигнал, полученный на базе наклона зигзага в диапазоне [-1;1]. Сдвигаем сигнал на один бар влево (в будущее). Именно по этому сигналу мы будем обучать нейросеть.
Вычисляем сигналы для ZZ с длиной колен не менее 37 пунктов (4 знака).
> out <- ZZ(ch = 37, mode = "m") Loading required package: TTR Loading required package: magrittr > table(out[ ,2]) -1 1 2828 3162
Как видим, классы незначительно разбалансированы. При формировании наборов для обучения модели мы примем меры для их выравнивания.
2.3. Исходный датафрейм
Напишем функцию, которая будет создавать исходный датафрейм, очищать его от неопределенных данных (NA) и преобразует целевую переменную в фактор с двумя классами «-1» и «+1». Эта функция объединяет в себе ранее описанные функции In() и ZZ(). Сразу отрежем последние 500 баров, по которым и будем определять качество предсказания модели.
#-----4--------------------------------- form.data <- function(n = 16, z = 37, len = 500){ require(magrittr) x <- In(p = n) out <- ZZ(ch = z, mode = "m") data <- cbind(x, y = out[ ,2]) %>% as.data.frame %>% head(., (nrow(x)-len))%>% na.omit data$y <- as.factor(data$y) return(data) }
2.3.1. Удаление высококоррелированных переменных
Удалим из нашего исходного набора переменные с коэффициентом корреляции выше 0.9. Напишем функцию, которая будет формировать исходный датафрейм, удалять из него высококоррелированные переменные и возвращать очищенные данные.
Можем предварительно посмотреть, какие переменные имеют корреляцию выше 0.9.
> data <- form.data(n = 16, z = 37) # подготовим датафрейм > descCor <- cor(data[ ,-ncol(data)])# уберем из него целевую > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.1887 0.0532 0.2077 0.3040 0.5716 0.9588 > highCor <- caret::findCorrelation(descCor, cutoff = 0.9) > highCor [1] 12 9 15 > colnames(data[ ,highCor]) [1] "rsi" "cmo" "SMI"
Таким образом, удалению подлежат приведенные выше переменные. Очистим от них датафрейм.
> data.f <- data[ ,-highCor] > colnames(data.f) [1] "DX" "ADX" "oscDX" "ar" "tr" [6] "atr" "cci" "chv" "sign" "vsig" [11] "slowD" "oscK" "signal" "vol" "Class"
Запишем это компактно, одной функцией:
#---5----------------------------------------------- cleaning <- function(n = 16, z = 37, cut = 0.9){ data <- form.data(n, z) descCor <- cor(data[ ,-ncol(data)]) highCor <- caret::findCorrelation(descCor, cutoff = cut) data.f <- data[ ,-highCor] return(data.f) } > data.f <- cleaning()
Не все авторы пакетов и исследователи согласны с тем, что нужно удалять высококоррелированные данные из наборов. Однако здесь нужно сравнивать результаты с применением обеих вариантов. В нашем случае выберем вариант с удалением.
2.4. Выбор наиболее важных переменных
Выбор важных переменных будем производить по трем показателям: глобальной важности, локальной важности (во взаимодействии) и частичной важности по классам. Будем использовать возможности пакета "randomUniformForest", подробно описанные в предыдущей статье. Соберем все предыдущие и последующие действия в одну функцию для компактности. Т.е., выполнив ее, мы получим в результате три набора:
- с лучшими переменными по вкладу и взаимодействию;
- с лучшими переменными для класса «-1»;
- с лучшими переменными для класса «+1».
#-----6------------------------------------------------ prepareBest <- function(n, z, cut, method){ require(randomUniformForest) require(magrittr) data.f <<- cleaning(n = n, z = z, cut = cut) idx <- rminer::holdout(y = data.f$Class) prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)], method = method) x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)]) x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)]) y.train <- data.f[idx$tr, ncol(data.f)] y.test <- data.f[idx$ts, ncol(data.f)] #--------- ruf <- randomUniformForest( X = x.train, Y = y.train, xtest = x.test, ytest = y.test, mtry = 1, ntree = 300, threads = 2, nodesize = 1 ) imp.ruf <- importance(ruf, Xtest = x.test) best <- imp.ruf$localVariableImportance$classVariableImportance %>% head(., 10) %>% rownames() #-----partImport best.sell <- partialImportance(X = x.test, imp.ruf, whichClass = "-1", nLocalFeatures = 7) %>% row.names() %>% as.numeric() %>% colnames(x.test)[.] best.buy <- partialImportance(X = x.test, imp.ruf, whichClass = "1", nLocalFeatures = 7) %>% row.names() %>% as.numeric() %>% colnames(x.test)[.] dt <- list(best = best, buy = best.buy, sell = best.sell) return(dt) }
Поясним порядок вычислений функции. Формальные параметры:
n – параметр входных данных;
z – параметр выходных данных;
cut – порог корреляции переменных;
method – метод препроцессинга входных данных.
Вычисления по порядку:
- создаем исходный набор данных data.f , у которого удалены высококоррелированные переменные, и сохраним его для дальнейшего использования;
- определяем индексы тренировочного и тестового набора idx ;
- определяем параметры препроцессинга prep ;
- разделяем исходный набор на тренировочный и тестовый, входные данные нормируем;
- обучаем и тестируем модель ruf на полученных наборах;
- вычисляем важность переменных imp.ruf ;
- выбираем 10 наиболее важных переменных по вкладу и взаимодействию best ;
- отбираем по 7 наиболее важных переменных для класса «-1» и «+1» best.buy, best.sell ;
- формируем лист с тремя наборами предикторов best, best.buy, best.sell.
Вычислим эти наборы и оценим значение глобальной, локальной и частичной важности отобранных переменных.
> dt <- prepareBest(16, 37, 0.9, c("center", "scale","spatialSign")) Loading required package: randomUniformForest Labels -1 1 have been converted to 1 2 for ease of computation and will be used internally as a replacement. 1 - Global Variable Importance (14 most important based on information gain) : Note: most predictive features are ordered by 'score' and plotted. Most discriminant ones should also be taken into account by looking 'class' and 'class.frequency'. variables score class class.frequency percent 1 cci 4406 -1 0.51 100.00 2 signal 4344 -1 0.51 98.59 3 ADX 4337 -1 0.51 98.43 4 sign 4327 -1 0.51 98.21 5 slowD 4326 -1 0.51 98.18 6 chv 4296 -1 0.52 97.51 7 oscK 4294 -1 0.52 97.46 8 vol 4282 -1 0.51 97.19 9 ar 4271 -1 0.52 96.95 10 atr 4237 -1 0.51 96.16 11 oscDX 4200 -1 0.52 95.34 12 DX 4174 -1 0.51 94.73 13 vsig 4170 -1 0.52 94.65 14 tr 4075 -1 0.50 92.49 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 7 14 7 2 - Local Variable importance Variables interactions (10 most important variables at first (columns) and second (rows) order) : For each variable (at each order), its interaction with others is computed. cci slowD atr tr DX atr 0.1804 0.1546 0.1523 0.1147 0.1127 cci 0.1779 0.1521 0.1498 0.1122 0.1102 slowD 0.1633 0.1375 0.1352 0.0976 0.0956 DX 0.1578 0.1319 0.1297 0.0921 0.0901 vsig 0.1467 0.1209 0.1186 0.0810 0.0790 oscDX 0.1452 0.1194 0.1171 0.0795 0.0775 tr 0.1427 0.1168 0.1146 0.0770 0.0750 oscK 0.1381 0.1123 0.1101 0.0725 0.0705 sign 0.1361 0.1103 0.1081 0.0704 0.0685 signal 0.1326 0.1068 0.1045 0.0669 0.0650 avg1rstOrder 0.1452 0.1194 0.1171 0.0795 0.0775 vsig oscDX oscK signal ar atr 0.1111 0.1040 0.1015 0.0951 0.0897 cci 0.1085 0.1015 0.0990 0.0925 0.0872 slowD 0.0940 0.0869 0.0844 0.0780 0.0726 DX 0.0884 0.0814 0.0789 0.0724 0.0671 vsig 0.0774 0.0703 0.0678 0.0614 0.0560 oscDX 0.0759 0.0688 0.0663 0.0599 0.0545 tr 0.0733 0.0663 0.0638 0.0573 0.0520 oscK 0.0688 0.0618 0.0593 0.0528 0.0475 sign 0.0668 0.0598 0.0573 0.0508 0.0455 signal 0.0633 0.0563 0.0537 0.0473 0.0419 avg1rstOrder 0.0759 0.0688 0.0663 0.0599 0.0545 chv vol sign ADX avg2ndOrder atr 0.0850 0.0850 0.0847 0.0802 0.1108 cci 0.0824 0.0824 0.0822 0.0777 0.1083 slowD 0.0679 0.0679 0.0676 0.0631 0.0937 DX 0.0623 0.0623 0.0620 0.0576 0.0881 vsig 0.0513 0.0513 0.0510 0.0465 0.0771 oscDX 0.0497 0.0497 0.0495 0.0450 0.0756 tr 0.0472 0.0472 0.0470 0.0425 0.0731 oscK 0.0427 0.0427 0.0424 0.0379 0.0685 sign 0.0407 0.0407 0.0404 0.0359 0.0665 signal 0.0372 0.0372 0.0369 0.0324 0.0630 avg1rstOrder 0.0497 0.0497 0.0495 0.0450 0.0000 Variable Importance based on interactions (10 most important) : cci atr slowD DX tr vsig oscDX 0.1384 0.1284 0.1182 0.0796 0.0735 0.0727 0.0677 oscK signal sign 0.0599 0.0509 0.0464 Variable importance over labels (10 most important variables conditionally to each label) : Class -1 Class 1 cci 0.17 0.23 slowD 0.20 0.09 atr 0.14 0.15 tr 0.04 0.12 oscK 0.08 0.03 vsig 0.06 0.08 oscDX 0.04 0.08 DX 0.07 0.08 signal 0.05 0.04 ar 0.04 0.02
Результаты
- По глобальной важности все 14 входных переменных равны.
- Суммарно по вкладу (глобальная важность) и по взаимодействию(локальная важность) определены 10 лучших.
- Семь наилучших переменных по частичной важности для каждого класса приведены ниже на графиках.
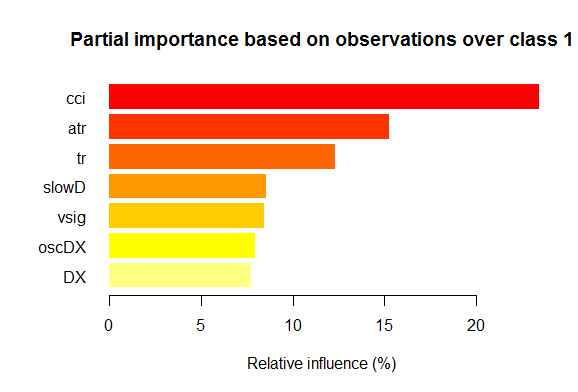
Рис. 2. Частичная важность переменных для класса "1"
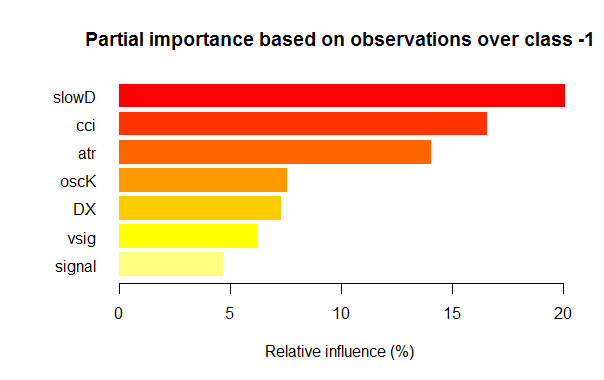
Рис. 3. Частичная важность переменных для класса "-1"
Как видим, для разных классов наиболее важные переменные отличаются как по составу, так и по ранжированию. Так, если для класса «-1» наиболее важна переменная slowD, то для класса «+1» она только на 4 месте.
Итак, у нас готовы наборы данных. Теперь можем приступать к экспериментам.
3. Экспериментальная часть.
Эксперименты будем проводить в среде языка R, точнее Revolution R Open, version 3.2.2, дистрибутив фирмы Revolution Analytics. http://www.revolutionanalytics.com/revolution-r-open
Этот дистрибутив имеет ряд преимуществ перед обычным R 3.2.2:
- быстрые и более качественные вычисления за счет применения multi-threaded processing with Intel® Math Kernel Library ;
- расширенные возможности с Reproducible R Toolkit . Небольшое пояснение: язык R активно развивается, постоянно улучшая существующие пакеты и добавляя новые. Обратная сторона такого прогресса — потеря воспроизводимости. Т.е., ваши продукты, написанные несколько месяцев назад и хорошо работавшие, после очередного обновления пакетов вдруг перестают работать. Приходится терять море времени для выявления и ликвидации ошибки, вызванной изменением в каком-то либо из пакетов. К примеру, в первой статье по глубоким нейросетям был приложен эксперт, который на момент написания отлично работал. Однако уже через несколько месяцев после публикации ряд пользователей сообщили о его неработоспособности. Анализ показал, что обновление пакета "svSocket" привело к сбою работы эксперта, причину которого я так и не нашел. Доработанный эксперт будет приложен к этой статье. Эта проблема стала чрезвычайно актуальна, и в Revolution Analytics решили ее просто. Теперь при выпуске нового дистрибутива фиксируется состояние всех пакетов в депозитарии CRAN на дату выхода дистрибутива путем копирования их на свое зеркало. Никакие изменения в депозитарии CRAN после этой даты не влияют на пакеты, «замороженные» на зеркале Revolution. Кроме того, начиная с октября 2014 года, фирма делает ежедневные снимки депозитария CRAN, фиксируя актуальное состояние и версии пакетов. С помощью их же пакета "checkpoint" мы теперь можем загрузить нужные нам пакеты, актуальные на нужную нам дату. Иными словами, мы имеем своеобразную мини-машину времени.
И еще одна новость. Девять месяцев назад Microsoft купила Revolution Analytics, пообещав при этом поддерживать их разработки, оставив дистрибутив Revolution R Open (RRO) доступным без оплаты. После этого последовал ряд сообщений о новинках в RRO и Revolution R Enterpise (не говоря уже об интеграции R с SQL Server, PowerBI, Azure и Cortana Analitics). Теперь у нас есть сообщение о том, что следующее обновление RRO будет называться Microsoft R Open а Revolution R Enterprise будет Microsoft R Server. Ну и буквально в последние дни Microsoft R объявила : R идет в Visual Studio. R Tools for Visual Studio (RTVS) следует модели Python Tools for Visual Studio. Это будет бесплатное дополнение к Visul Studio которое предоставит комплектное IDE для R, с возможностью редактирования и интерактивной отладки скриптов.
На момент окончания написания статьи уже вышла Microsoft R Open (R 3.2.3), поэтому в дальнейшем в статье мы будем использовать пакеты для этой версии.
3.1. Построение моделей
3.1.1. Краткое описание пакета "darch"
Пакет "darch" ver. 0.10.0 предоставляет широкий круг функций, позволяющих не просто создать и обучить модель, но буквально по кирпичикам сложить и настроить её под Ваши предпочтения. Как указано ранее, глубокая сеть состоит из n-го количества RBM (n = layers -1) и нейросети MLP с количеством слоев layers. Послойное предобучение RBM производится на неразмеченных данных без учителя. Тонкое обучение нейросети производится с учителем на размеченных данных. Разделение этих стадий обучения дает нам возможность использовать различные по объему (но не по структуре!) данные или получить несколько различных тонко обученных моделей на базе одного предобучения. Кроме того, если данные для предобучения и тонкой настройки одинаковы, возможно провести обучение одним ходом без разделения на две стадии. Можно пропустить предобучение и использовать только многослойную нейросеть или, наоборот, использовать только RBM без нейросети. При этом у нас есть доступ ко всем внутренним параметрам. Пакет предназначен для продвинутых пользователей. Дальше мы будем рассматривать раздельные процессы: претренинг и тонкую настройку.
3.1.2. Построение модели DBN. Параметры.
Опишем порядок построения, обучения и тестирования модели DBN.
newDArch(layers, batchSize, ff=FALSE, logLevel=INFO, genWeightFunc=generateWeights),
где:
- layers : массив с указанием количества слоев и нейронов в каждом слое. Например : layers = c(5,10,10,2) – входной слой с 5 нейронами (видимыми), два скрытых слоя с 10 нейронами в каждом, и один выходной слой с 2 выходами.
- BatchSize : размер минивыборки при обучении.
- ff : указывает, использовать ли формат ff для весов, смещения и выходов. Формат ff применяется для сжатого сохранения больших данных.
- LogLevel : уровень логирования и вывода информации при исполнении функции.
- GenWeightFunction: функция для генерирования матрицы весов RBM. Есть возможность использовать пользовательскую функцию активации.
В созданном darch-объекте содержится (layers - 1) RBM, объединенных в накапливающую сеть, которые будут использоваться для претренинга нейросети. Два атрибута fineTuneFunction и executeFunction содержат функции для тонкой настройки (по умолчанию backpropagation) и для исполнения ( по умолчанию runDarch). Обучение сети осуществляется с помощью двух обучающих функций preTrainDArch() и fineTuneDArch(). Первая функция тренирует сеть RBM без учителя методом сравнительного расхождения (contrastive divergence). Вторая функция использует функцию, указанную в атрибуте fineTuneFunction для тонкой настройки нейросети . После выполнения нейросети, выходы каждого слоя могут быть найдены в атрибуте executeOutputs или только выходного слоя в атрибуте executeOutput .
2. Функция претренинга darch-объекта
preTrainDArch(darch, dataSet, numEpoch = 1, numCD = 1, ..., trainOutputLayer = F),где:
- darch: экземпляр класса 'Darch';
- dataSet : набор данных для обучения ;
- numEpoch : количество эпох обучения;
- numCD : количество итераций сэмплинга. Как правило, достаточно одной;
- ... : дополнительные параметры, которые можно передать функции trainRBM;
- trainOutputLayer : логическая величина показывающая тренировать ли выходной слой RBM.
Функция исполняет для каждой RBM обучающую функцию trainRBM(), копируя после обучения веса и смещения (biases) в соответствующие слои нейросети darch-объекта.
3. Функция тонкой настройки darch-объектаfineTuneDArch(darch, dataSet, dataSetValid = NULL, numEpochs = 1, bootstrap = T,
isBin = FALSE, isClass = TRUE, stopErr = -Inf, stopClassErr = 101,
stopValidErr = -Inf, stopValidClassErr = 101, ...),
где:
- darch: экземпляр класса 'Darch';
- dataSet : набор данных для обучения (возможно использовать и для валидации) и тестирования;
- dataSetValid : набор данных, используемых для валидации;
- numxEpoch : количество эпох обучения;
- bootstrap : логическая, нужно ли применять бутсрапинг при создании валидационых данных;
- isBin : указывает, должны ли выходные данные интерпретироваться как логические значения. По умолчанию — FALSE. Если TRUE, каждое значение больше 0.5 интерпретируется как 1, а меньше — как 0.
- isClass : указывает, обучается ли сеть для классификации. Если TRUE, то статистики для классификации будут определены. По умолчанию TRUE.
- stopErr : критерий остановки обучения нейросети по ошибке при обучении. По умолчанию -Inf;
- stopClassErr : критерий остановки обучения нейросети по ошибке классификации при обучении. По умолчанию 101;
- stopValidErr : критерий остановки нейросети по ошибке на валидационых данных. По умолчанию -Inf;
- stopValidClassErr : критерий остановки нейросети по ошибке классификации при валидации. По умолчанию 101;
- ... : дополнительные параметры , которые можно передать функции обучения.
Функция обучает заданную сеть функцией, сохраненной в атрибуте fineTuneFunction darch-объекта. Входные данные (trainData, validData, testData) и принадлежащие им классы (targetData, validTargets, testTargets) могут быть переданы как dataSet или ff-матрица. Данные и классы для валидации и тестирования не являются обязательными. Если они будут предоставлены, то нейросеть будет исполнена с этими наборами данных и статистики будут вычислены. Атрибут isBin указывает, должны ли выходные данные интерпретироваться как двоичные. Если isBin = TRUE, каждое выходное значение больше 0.5 интерпретируется как 1, а в противном случае — как 0. Также можно установить критерий остановки для обучения по ошибке (stopErr, stopValidErr) или правильной классификации (stopClassErr, stopValidClassErr) на обучающем или валидационном наборах.
Все параметры функций имеют значения по умолчанию. Однако доступны и другие значения. Так, например:
Функция активации нейронов — доступны sigmoidUnitDerivative, linearUnitDerivative, softmaxUnitDerivative, tanSigmoidUnitDerivative. По умолчанию — sigmoidUnitDerivative.
Функции тонкой настройки нейросети — по умолчанию обратное распространение ошибки (backpropagation), доступно также эластичное обратное распространение ошибки rpropagation (resilient-propagation) в четырех вариантах ("Rprop+", "Rprop-", "iRprop+", "iRprop-") и minimizeClassifier (эта функция тренируется классификатором сети Darch по методу сопряженных градиентов). Для последних двух алгоритмов и для тех, кто глубоко в теме, предусмотрена отдельная реализация тонкой настройки нейросети с возможностью настройки множества их параметров. Например:
rpropagation(darch, trainData, targetData, method="iRprop+",
decFact=0.5, incFact=1.2, weightDecay=0, initDelta=0.0125,
minDelta=0.000001, maxDelta=50, ...),
где:
- darch – darch-объект для обучения;
- trainData – набор входных данных для обучения;
- targetData – ожидаемый выход для обучающего набора;
- method – метод для обучения. По умолчанию "iRprop+". Возможны "Rprop+", "Rprop-", "iRprop-";
- decFact – уменьшающий фактор для обучения. По умолчанию 0.5;
- incFact - увеличивающий фактор для обучения. По умрлчанию 1.2;
- weightDecay – уменьшение веса при обучении. По умолчанию 0;
- initDelta – значение инициализации при обновлении. По умолчанию 0.0125;
- minDelta – нижняя граница для размера шага. По умолчанию 0.000001;
- maxDelta – верхняя граница для размера шага. По умолчанию 50.
Функция возвращает darch-объект с обученной нейросетью.
3.2. Формирование обучающей и тестовой выборок.
Мы уже сформировали исходный набор данных. Теперь нам необходимо разделить его на тренировочный, валидационный и тестовый. Соотношение по умолчанию 2/3. В различных пакетах представлено много функций, выполняющих такое разделение. Я использую функцию rminer::holdout(), которая вычисляет индексы для разделения исходного набора на тренировочный и тестовый.
holdout(y, ratio = 2/3, internalsplit = FALSE, mode = "stratified", iter = 1,
seed = NULL, window=10, increment=1),
где:
- y – желаемая целевая переменная, числовой вектор или фактор, в этом случае применяется стратифицированное разделение (т.е., пропорции между классами одинаковы для всех частей);
- ratio – соотношение раздела (в процентах — устанавливается размер тренировочного набора; или в общем количестве экземпляров — устанавливается размер тестового набора);
- internalsplit – если TRUE, то тренировочные данные разделяются еще раз на тренировочный и валидационный набор. То же самое ratio применяется для внутреннего разделения;
- mode – режим сэмплинга. Возможны опции:
- stratified – стратифицированное случайное разделение (если у фактор; иначе стандартное случайное разделение);
- random – стандартное случайное разделение;
- order – статичный режим, когда первые экземпляры используются для тренировки а оставшиеся — для тестирования (широко применяется для таймсерий);
- rolling – подвижное окно, более известное как скользящее окно (широко применяется при предсказании фондовых и финансовых рынков), аналогично order, за исключением того, что window – размер окна, iter – роллинг итерации и increment — количество примеров, на которое окно проскальзывает вперед на каждой итерации. На каждой итерации размер тренировочного набора фиксируется window, тогда как тестовый набор эквивалентен ratio, за исключением последней итерации (где он может быть меньше).
- incremental – инкрементальный режим переобучения, известный также и как растущее окно, аналогично order за исключением того, что window — начальный размер окна, iter — инкрементальные итерации и increment — число примеров, добавляемых на каждой итерации. В каждой итерации размер тренировочного набора растет (+increment), тогда как размер тестового набора эквивалентен ratio, за исключением последней итерации, когда он может быть меньше.
- iter – количество итераций инкрементального режима переобучения (используется только когда mode = "rolling" или "incremental", обычно iter устанавливается в цикле).
- seed – если NULL, то используется random seed, иначе seed фиксируется (при последующих вычислениях будет возвращаться всегда один и тот же результат);
- window – размер тренировочного окна ( если mode = "rolling") или начальный размер тренировочного окна (если mode = "incremental");
- increment – количество примеров, добавляемых к тренировочному окну на каждой итерации (если mode="incremental" или mode="rolling").
3.2.1. Балансировка классов и препроцессинг.
Напишем функцию, которая выровняет (при необходимости) количество классов в выборке в большую сторону, разделит выборку на тренировочный и тестовый набор, проведет препроцессинг (нормирование, при необходимости) и вернет лист с соответствующими наборами train, test. Для балансировки будем использовать функцию caret::upSample(), которая добавляет образцы, извлеченные случайным образом с заменой, делая распределение классов одинаковым. Нужно сказать, что не все исследователи признают необходимость в балансировке классов. Но, как известно, практика — критерий истины, а по результатам моих многочисленных экспериментов балансированные наборы всегда показывают лучшие результаты в обучении. Но это не мешает вам самостоятельно поэкспериментировать.
Для препроцессинга будем использовать функцию caret::preProcess(). Параметры препроцессинга сохраним в переменной prepr. Поскольку мы их уже рассматривали и применяли в предыдущих статьях , я не буду останавливаться на их описании.
#---7---------------------------------------------------- prepareTrain <- function(x , y, rati, mod = "stratified", balance = F, norm, meth) { require(magrittr) require(dplyr) t <- rminer::holdout(y = y, ratio = rati, mode = mod) train <- cbind(x[t$tr, ], y = y[t$tr]) if(balance){ train <- caret::upSample(x = train[ ,best], y = train$y, list = F)%>% tbl_df train <- cbind(train[ ,best], select(train, y = Class)) } test <- cbind(x[t$ts, ], y = y[t$ts]) if (norm) { prepr <<- caret::preProcess(train[ ,best], method = meth) train = predict(prepr, train[ ,best])%>% cbind(., y = train$y) test = predict(prepr, test[ ,best] %>% cbind(., y = test$y)) } DT <- list(train = train, test = test) return(DT) }
Замечание по препроцессингу: входные переменные будем нормировать в диапазон (-1, 1).
3.2.2. Кодирование целевой переменной
При решении задачи классификации целевая переменная — фактор с несколькими уровнями (классами). В модели она задается вектором (столбцом), состоящим из последовательных состояний целевой. Например, y = с("1", "1", "2", "3", "1"). Для подачи нейросети на обучение целевую переменную нужно закодировать (преобразовать) в матрицу с количеством столбцов, равным количеству классов. В каждой строке такой матрицы только в одном столбце может быть единица. Такое преобразование наряду с использованием в выходном слое функции активации softmax() позволяет получить вероятности состояния предсказанной целевой в каждом классе. Кодирование будем производить с помощью функции classvec2classmat(). Нужно сказать, что это не единственный и не лучший метод кодирования целевой, но для простоты мы будем применять именно его. Обратное преобразование (декодирование) предсказанных значений целевой возможно несколькими способами, о которых мы поговорим позже.
3.3. Обучение модели
3.3.1. Претренинг
Как мы говорили выше, сначала создаем объект глубокой архитектуры DArch, который включает в себя необходимое количество RBM с параметрами предварительного обучения по умолчанию и нейросеть, инициированную случайными весами и функцией активации нейронов, установленной по умолчанию. На этапе создания объекта, если необходимо, можно изменить параметры претренинга. После этого проводим предварительное обучение сети RBM без учителя, подав на вход обучающий набор (без целевой переменной). По окончанию претренинга мы получим DАrch, в котором веса и смещения, полученные при обучении RBM, перенесены в нейросеть. Предварительно нам нужно задать расклад скрытых нейронов в слоях в виде вектора (например):
L<- c( 14, 50, 50, 2)
Количество нейронов во входном слое равно количеству входных переменных. Два скрытых слоя будут содержать по 50 нейронов, выходной слой — с двумя нейронами. Последнее немного поясню. Если целевая переменная (фактор) имеет два уровня (класса), то, в принципе, можно обойтись и одним выходом. Но перевод вектора в матрицу с двумя столбцами, каждый из которых соответствует одному классу, позволяет нам применить в выходном слое функцию активации softmax(), которая отлично работает в задачах классификации. Кроме того, выходы в виде вероятностей классов дают нам дополнительные возможности в последующем анализе результатов. Ниже мы поговорим об этом.
Количество эпох при обучении устанавливаем экспериментальным путем, как правило — в пределах 10-50.
Количество итераций сэмплинга оставим по умолчанию, но можно поэкспериментировать, увеличив этот параметр. Оформим это отдельной функцией:
#----8-------------------------------------------------------------- pretrainDBN <- function(L, Bs, dS, nE, nCD, InM = 0.5, FinM = 0.9) { require(darch) # создаем объект DArch dbn <- newDArch(layers = L, batchSize = Bs, logLevel = 5) # устанавливаем начальный момент setInitialMomentum(dbn) <- InM # устанавливаем финальный момент setFinalMomentum(dbn) <- FinM # устанавливаем время переключения моментов с начального на финальный setMomentumSwitch(dbn) <- round(0.8 * nE) dbn <- preTrainDArch(dbn, dataSet = dS, numEpoch = nE, numCD = nCD, trainOutputLayer = T) return(dbn) }
3.3.2. Тонкое обучение
Как мы говорили выше, для тонкого обучения пакет предлагает функции — backpropagation(), rpropagation(), minimizeClassifier(), minimizeAutoencoder(). Две последних мы не будем рассматривать, так как они недостаточно документированы в пакете, и отсутствуют примеры их применения. В моих экспериментах эти функции не показали хороших результатов.
Дополнительно хочу еще раз сказать об обновлениях пакетов. В начале написания статьи текущей версией была 0.9, а в момент окончания вышла новая версия 0.10, в которой произошли значительные изменения. Пришлось переделывать все расчеты. По результатам недолгого тестирования могу сказать, что скорость работы значительно возросла, чего не могу сказать о качестве результатов (что, в общем-то, не вина пакета, а вина применяющего).
Рассмотрим две первые функции. Первая (backpropagation) установлена по умолчанию в объекте DАrch и использует параметры обучения нейросети, предоставленные здесь же. Вторая (rpropagation) также имеет параметры по умолчанию и четыре метода обучения (выше я описывал их) по умолчанию "iRprop+" . Конечно, и параметры и метод обучения Вы можете изменить. Применять эти функции просто: замените в функции FineTuneDarch() функцию тонкого обучения
setFineTuneFunction(dbn) <- rpropagation
Кроме функции тонкой настройки, мы должны установить (при необходимости) функции активации нейронов в каждом слое. Мы помним, что по умолчанию во всех слоях установлены sigmoidUnit. Доступны в пакете sigmoidUnitDerivative, linearUnitDerivative, tanSigmoidUnitDerivative, softmaxUnitDerivative . Оформим тонкую настройку отдельной функцией с возможностью выбора функции токной настройки. Соберем возможные функции активации в отдельный список :
actFun <- list(sig = sigmoidUnitDerivative, tnh = tanSigmoidUnitDerivative, lin = linearUnitDerivative, soft = softmaxUnitDerivative)
Напишем функцию тонкой настройки нейросети, которая будет тренировать и выдавать две нейросети: одну — обученную с помощью функции backpropagation, а вторую — с помощью функции rpropagation:
#-----9----------------------------------------- fineMod <- function(variant=1, dbnin, dS, hd = 0.5, id = 0.2, act = c(2,1), nE = 10) { setDropoutOneMaskPerEpoch(dbnin) <- FALSE setDropoutHiddenLayers(dbnin) <- hd setDropoutInputLayer(dbnin) <- id layers <<- getLayers(dbnin) stopifnot(length(layers)==length(act)) if(variant < 0 || variant >2) {variant = 1} for(i in 1:length(layers)){ fun <- actFun %>% extract2(act[i]) layers[[i]][[2]] <- fun } setLayers(dbnin) <- layers if(variant == 1 || variant == 2){ # backpropagation if(variant == 2){# rpropagation #setDropoutHiddenLayers(dbnin) <- 0.0 setFineTuneFunction(dbnin) <- rpropagation } mod = fineTuneDArch(darch = dbnin, dataSet = dS, numEpochs = nE, bootstrap = T) return(mod) } }
Несколько пояснений по формальным параметрам функции.
- variant - выбор функции тонкой настройки (1- backpropagation, 2- rpropagation).
- dbnin - модель получения в результате претренинга.
- dS - набор данных для тонкой настройки (dataSet).
- hd - коэффициент прореживания (hiddenDropout) в скрытых слоях нейросети.
- id - коэффициент прореживания (inputDropout) во входном слое нейросети.
- act - вектор с указанием функции активации нейронов в каждом слое нейросети. Длина вектора на единицу меньше количества слоев.
- nE - количество эпох обучения.
dataSet — новая сущность, появившаяся в этой версии. Цель ее появления для меня не до конца понятна. Стандартно в языке принято два способа подачи переменных в модель — парой (x, y) или формулой (y~., data). Появление этой сущности ничего не добавляет качественно, но запутывает пользователей. Хотя у автора могут быть другие резоны, мне не известные.
3.4. Тестирование модели. Метрики.
Тестирование обученной модели проводим на тестовых наборах. Нужно учитывать, что мы будем вычислять две метрики: формальную Accuracy и качественную K. О ней и поговорим ниже. Для этого нам потребуется два различных набора данных, и вот почему. Для вычисления Accuracy нам нужны значения целевой переменной, а ЗигЗаг, как мы помним, на последних барах чаще всего не определен. Поэтому тестовый набор для определения Accuracy мы будем определять функцией prepareTrain(), а для определения качественных показателей — функцией
#---10------------------------------------------- prepareTest <- function(n, z, norm, len = 501) { x <- In(p = n ) %>% na.omit %>% extract( ,best) %>% tail(., len) CO <- price[ ,"CO"] %>% tail(., len) if (norm) { x <- predict(prepr,x) } dt <- cbind(x = x, CO = CO) %>% as.data.frame() return(dt) }
Тестировать модели будем на последних 500 барах истории.
Само же тестирование проведем двумя функцями testAcc() и testBal().
#---11----- testAcc <- function(obj, typ = "bin"){ x.ts <- DT$test[ ,best] %>% as.matrix() y.ts <- DT$test$y %>% as.integer() %>% subtract(1) out <- predict(obj, newdata = x.ts, type = typ) if (soft){out <- max.col(out)-1} else {out %<>% as.vector()} acc <- length(y.ts[y.ts == out])/length(y.ts) %>% round(., digits = 4) return(list(Acc = acc, y.ts = y.ts, y = out)) } #---12----- testBal <- function(obj, typ = "bin") { require(fTrading) x <- DT.test[ ,best] CO <- DT.test$CO out <- predict(obj, newdata = x, type = typ) if(soft){out <- max.col(out)-1} else {out %<>% as.vector()} sig <- ifelse(out == 0, -1, 1) sig1 <- Hmisc::Lag(sig) %>% na.omit bal <- cumsum(sig1 * tail(CO, length(sig1))) K <- tail(bal, 1)/length(bal) * 10 ^ Dig Kmax <- max(bal)/which.max(bal) * 10 ^ Dig dd <- maxDrawDown(bal) return(list(sig = sig, bal = bal, K = K, Kmax = Kmax, dd = dd)) }
Первая функция возвращает собственно Acc и значения целевой переменной (реальное и предсказанное) для возможного последующего анализа. Вторая возвращает предсказанные сигналы для эксперта sig, баланс, полученный по этим сигналам bal, коэффициент качества К, максимальное значение этого коэффмцмента на тестируемом участке Kmax и максимальную просадку dd на том же участке .
При вычислении баланса необходимо помнить, что последний предсказанный сигнал относится к будущему, еще не сформировавшемуся бару, поэтому его нужно при расчетах удалить. Мы это сделали, сдвинув вектор sig вправо на один бар.
3.4.1. Декодирование предсказания.
Декодировать полученный результат (перевести из матрицы в вектор) можно способом "WTA". Класс равен номеру столбца с максимальным значением вероятности, при этом можно установить порог значения этой вероятности, ниже которого класс не определен.
out <- classmat2classvec(out, threshold = 0.5) или out <- max.col(out)-1
Если установить порог равным 0.5 и наибольшая вероятность в столбцах будет меньше этого порога, мы получим дополнительный класс "не_определен". Это нужно учитывать при вычислении таких метрик, как Accuracy.
3.4.2. Улучшение результата предсказания
Можно ли улучшить результат предсказания уже после его получения? Можно использовать следующие три возможности.
- Калибровка
CORElearn::calibrate(correctClass, predictedProb, class1 = 1, method = c("isoReg", "binIsoReg", "binning", "mdlMerge"), weight=NULL, noBins=10, assumeProbabilities=FALSE)
где:
- correctClass – вектор с корректными метками классов для классификационных проблем;
- predictedProb – вектор с предсказанным классом 1 (вероятности) той же длины, что и correctClass;
- method — один из ("isoReg", "binIsoReg", "binning", "mdlMerge"). Подробности смотрите в описании пакета;
- weight — вектор (если он указан) должен быть той же длины, что и correctClass, и представлять вес каждого наблюдения, иначе по умолчанию веса всех наблюдений равны 1;
- noBins — значение параметра зависит от method и определяет желаемое или начальное количество каналов;
- assumeProbabilities — логическая, если TRUE, то значение в predictedProb ожидается в диапазоне [0, 1], т. е. оценкой вероятности, иначе алгоритм может быть использован как обычная изотоническая регрессия.
Этот способ применим в случае целевой переменной с двумя уровнями, заданными вектором.
- Сглаживание результатов предсказания с помощью модели Марковской цепи
Это очень обширная и сложная тема, достойная отдельной статьи, поэтому я не буду углубляться в теорию, только основные определения.
Марковский процесс – случайный процесс, обладающий следующим свойством: для любого момента времени t0 вероятность любого состояния системы в будущем зависит только от ее состояния в настоящем и не зависит от того, когда и каким образом система пришла в это состояние.
Классификация случайных марковских процессов:
- с дискретными состояниями и дискретным временем (цепь Маркова);
- с непрерывными состояниями и дискретным временем (марковские последовательности);
- с дискретными состояниями и непрерывным временем (непрерывная цепь Маркова);
- с непрерывным состоянием и непрерывным временем.
Здесь и далее рассматриваются только марковские процессы с дискретными состояниями S1, S2, ..., Sn.
Марковская цепь — марковский случайный процесс с дискретными состояниями и дискретным временем.
Моменты t1, t2, ..., когда система S может менять свое состояние, рассматривают как последовательные шаги процесса. В качестве аргумента, от которого зависит процесс, выступает не время t, а номер шага 1,2,...,k,...
Случайный процесс характеризуется последовательностью состояний S(0), S(1), S(2), ..., S(k), ..., где S(0) — начальное состояние (перед первым шагом); S(1) — состояние после первого шага; S(k) — состояние системы после k-го шага.
Вероятности состояний цепи Маркова – вероятности Pi(k) того, что после k-го шага (и до (k + 1)-го) система S будет находиться в состоянии Si,(i = 1 , 2 , ..., п).
Начальное распределение вероятностей марковской цепи — распределение вероятностей состояний в начале процесса.
Вероятность перехода (переходная вероятность) на k-м шаге из состояния Si в состояние Sj — условная вероятность того, что система S после k-го шага окажется в состоянии Sj, при условии, что непосредственно перед этим (после k—1 шага) она находилась в состоянии Si.
Переходные вероятности однородной цепи Маркова Рij образуют квадратную матрицу размера п х п. Ее особенности:
- Каждая строка характеризует выбранное состояние системы, а ее элементы — вероятности всех возможных переходов за один шаг из выбранного (из i-го) состояния.
- Элементы столбцов — вероятности всех возможных переходов за один шаг в заданное (j-е) состояние.
- Сумма вероятностей каждой строки равна единице.
- По главной диагонали — вероятности Рij того, что система не выйдет из состояния Si, а останется в нем.
Марковский процесс может быть наблюдаемым и скрытым. Скрытая Марковская Модель ( Hidden Markov Model(HMM)) состоит из пары дискретных стохастических процессов {St} и {Xt}. Наблюдаемый процесс {Xt} связан с ненаблюдаемым (скрытым) марковским процессом состояний {St} с помощью так называемых условных распределений.
Строго говоря, наблюдаемый марковский процесс состояний (классов) нашей целевой таймсерии не является однородным. Очевидно, что вероятность перехода из одного состояния в другое зависит от времени пребывания в текущем состоянии. Т.е. на первых шагах после изменения состояния вероятность его изменения низкая и возрастает с увеличением времени пребывания в состоянии. Такие модели называют полумарковскими (HSMM). В их рассмотрение углубляться мы не будем.
Идея состоит в следующем: на основе дискретной последовательности идеальных сигналов (целевой) полученных из ЗигЗага определим параметры НММ. Затем, имея предсказанные нейросетью сигналы, сгладим их с помощью НММ.
Что это нам дает? Как правило, в предсказании нейросети имеются т.н. "выбросы", участки изменения состояния длиной в один — два бара. Мы знаем, что целевая переменная не имеет столь малых длительностей. Приложив к предсказанной последовательности модель, полученную на целевой, мы можем привести ее к более вероятным переходам.
Для этих вычислений будем использовать пакет "mhsmm", предназначенный для вычислений скрытых Марковских и полумарковских моделей. Будем использовать функцию smooth.discrete(), производящую простое сглаживание таймсерии дискретных значений.
obj <- smooth.discrete(y)
Сглаженная последовательность состояний, полученная в результате по умолчанию — как наиболее вероятная последовательность состояний, полученная с помощью алгоритма Viterbi (т.н. глобальное декодирование). Предусмотрена возможность сглаживания другим методом smoothed, при этом будут определяться индивидульные наиболее вероятные состояния (т.н. локальное декодирование).
Для сглаживания новой таймсерии применяется стандартный метод
sm.y <- predict(obj, x = new.y)
- Корректировка предсказанных сигналов по кривой теоретического баланса
Идея состоит в следующем. Имея линию баланса, мы можем вычислить ее отклонение от средней. По этим отклонениям вычислим корректирующие сигналы. В моменты, когда отклонение уходит в минус, они или выключают выполнение предсказанных сигналов, или делают их противоположными. Идея в целом хороша, но есть одно "но". На нулевом баре у нас есть предсказанный сигнал, а значения баланса и, соответственно, корректировочного сигнала нет. Здесь есть два варианта решения: классификация — по существующим корректирующим сигналам и отклонениям предсказать корректирующий сигнал; регрессия — по существующим отклонениям на сформированных барах спрогнозировать отклонение на начавшемся баре и на его основании определить корректирующий сигнал. Можно пойти более простым путем и принять значение корректирующего сигнала для нового бара на основе уже сформированного.
Поскольку вышеперечисленные способы нам известны и опробованы, мы попробуем использовать возможности Марковских цепей. В недавно появившемся пакете "markovchain" предоставлен ряд функций, которые позволяют по наблюдаемому дискретному процессу определить параметры скрытой Марковской модели и сделать прогноз будущих состояний на несколько баров в будущее. Идея взята из этой статьи.
3.4.3. Метрики
Для оценки качества предсказания модели применяется целый ряд метрик (Accuracy, AUC, ROC и др.). В предыдущей статье я говорил, что формальные метрики в нашем случае не определяют качества. Цель и задача работы эксперта — получить максимальную прибыль с допустимой просадкой. Для этих целей был введен показатель качества К, который показывает среднюю прибыль в пунктах на один бар на фиксированном отрезке истории длиной N. Вычисляется он путем деления кумулятивного Return(sig, N) на длину отрезка N. Accuracy мы будем вычислять только индикативно.
Наконец, проведем вычисления и получим результаты тестирования:
- Исходные данные. У нас уже есть матрица price[], полученная в результате выполнения функции price.OHLC(). В ней содержатся котировки, средняя цена и тело баров. Все исходные можно получить, загрузив в Rstudio "картинку", которая находится в приложении.
# Определим константы n = 34; z = 37; cut = 0.9; soft = TRUE. # Определим метод препроцессинга method = c("center", "scale","spatialSign") # сформируем исходный набор данных data.f <- form.data(n = n, z = z) # определим набор важных предикторов best <- prepareBest(n = n, z = z, cut = cut, norm = T, method) # Вычисления занимают около 3 мин на 2-ядерном процессоре. Вы можете не выполнять этот этап, # а использовать весь набор предикторов в дальнейшем. Для этого закомментируйте предыдущую строку и # раскомментируйте две нижних. # data.f <- form.data(n = n, z = z) # best <- colnames(data.f) %>% head(., ncol(data.f) - 1) # Готовим набор для обучения нейросети DT <- prepareTrain(x = data.f[ , best], y = data.f$y, balance = TRUE, rati = 501, mod = "stratified", norm = TRUE, meth = method) # Загружаем необходимые библиотеки require(darch) require(foreach) # Определяем доступные функции активации actFun <- list(sig = sigmoidUnitDerivative, tnh = tanSigmoidUnitDerivative, lin = linearUnitDerivative, soft = softmaxUnitDerivative) # Преобразуем целевую переменную if (soft) { y <- DT$train$y %>% classvec2classmat()} # в матрицу if (!soft) {y = DT$train$y %>% as.integer() %>% subtract(1)} # в вектор со значениями [0, 1] # создаем dataSet для обучения dataSet <- createDataSet( data = DT$train[ ,best] %>% as.matrix(), targets = y , scale = F ) # Определяем константы для нейросети # Количество нейронов во входном слое (равно количеству предикторов) nIn <- ncol(dataSet@data) # Количество нейронов в выходном слое nOut <- ncol(dataSet@targets) # Вектор с количеством нейронов в каждом слое нейросети # Если Вы будете использовать другую структуру нейросети, этот вектор нужно переписать Layers = c(nIn, 2 * nIn , nOut) # Другие данные, относящиеся к обучению Bath = 50 nEp = 100 ncd = 1 # Претренинг нейросети preMod <- pretrainDBN(Layers, Bath, dataSet, nEp, ncd) # Дополнительные параметры для тонкой настройки Hid = 0.5; Ind = 0.2; nEp = 10 # Обучаем две модели, одну с backpropagation, другую — с rpropagation # Делаем это только для сравнения результатов model <- foreach(i = 1:2, .packages = "darch") %do% { dbn <- preMod if (!soft) {act = c(2, 1)} if (soft) {act = c(2, 4)} fineMod(variant = i, dbnin = dbn, hd = Hid, id = Ind, dS = dataSet, act = act, nE = nEp) } # Тестируем для получения Accuracy resAcc <- foreach(i = 1:2, .packages = "darch") %do% { testAcc(model[[i]]) } # Готовим набор данных для тестирования на коэффициент качества DT.test <- prepareTest(n = n, z = z, T) # Тестируем resBal <- foreach(i = 1:2, .packages = "darch") %do% { testBal(model[[i]]) }
Смотрим результат:
> resAcc[[1]]$Acc [1] 0.5728543 > resAcc[[2]]$Acc [1] 0.5728543
У обоих моделей он оказался одинаково плохим.
Но вот коэффициент качества —
> resBal[[1]]$K [1] 5.8 > resBal[[1]]$Kmax [1] 20.33673 > resBal[[2]]$Kmax [1] 20.33673 > resBal[[2]]$K [1] 5.8
показывает абсолютно одинаковые и при этом неплохие показатели. Правда, настораживает большая просадка:
> resBal[[1]]$dd$maxdrawdown [1] 0.02767
Попробуем скорректировать просадку с помощью корректирующего сигнала, полученного из расчета, приведенного ниже:
bal <- resBal[[1]]$bal # сигнал на последних 500 барах sig <- resBal[[1]]$sig[1:500] # средняя от линии баланса ma <- pracma::movavg(bal,16, "t") # момент от средней roc <- TTR::momentum(ma, 3)%>% na.omit # отклонение линии баланса от средней dbal <- (bal - ma) %>% tail(., length(roc)) # просуммируем два вектора dbr <- (roc + dbal) %>% as.matrix() # вычислим корректирующий сигнал sig.cor <- ifelse(dbr > 0, 1, -1) # sign(dbr) даст тот же результат # результирующий сигнал S <- sig.cor * tail(sig, length(sig.cor)) # баланс по результирующему сигналу Bal <- cumsum(S * (price[ ,"CO"]%>% tail(.,length(S)))) # коэффициент качества по откорректированному сигналу Kk <- tail(Bal, 1)/length(Bal) * 10 ^ Dig > Kk [1] 28.30382
Показанный результат качества по откорректированному сигналу очень хорош. Посмотрим, как выглядят на графике линии dbal, roc и dbr по которым мы вычисляем корректирующий сигнал.
matplot(cbind(dbr, dbal, roc), t="l", col=c(1,2,4), lwd=c(2,1,1)) abline(h=0, col=2) grid()
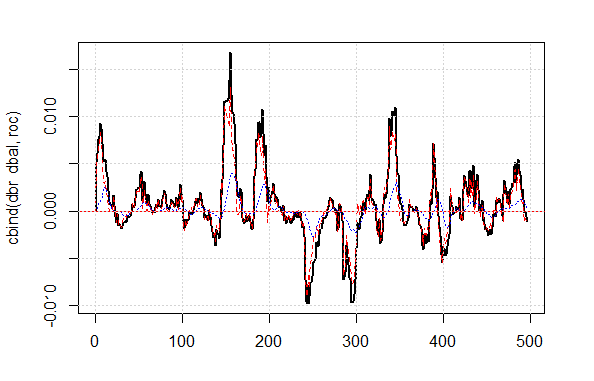
Рис.4 Отклонение линии баланса от средней
Линия баланса до корректировки сигналов и после приведена на рис. 5.
plot(c(NA,NA,NA,Bal), t="l") lines(bal, col= 2) lines(ma, col= 4)
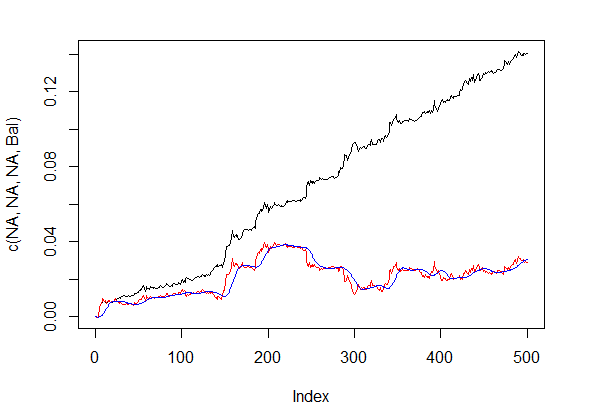
Рис.5 Линия баланса до и после корректировки сигналов
Итак, у нас есть предсказанное нейросетью значение сигнала на нулевом баре, но нет значения корректирующего. Мы хотим использовать скрытую модель Маркова для предсказания этого сигнала. По наблюдаемым состояниям корректирующего сигнала мы определим параметры модели и затем, используя значения нескольких последних состояний, предскажем состояние на один бар вперед. Для начала мы напишем функцию correct(), которая будет вычислять корректирующий сигнал по предсказанному, результирующий сигнал и качественные показатели по нему. Иными словами, компактно запишем расчеты, которые мы провели выше.
Хочу пояснить: под "сигналом" в статье понимается последовательность целых чисел -1 и 1. Под "состоянием" понимается последовательность целых чисел 1 и 2, соответствующих этим сигналам. Для взаимных преобразований будем использовать функции:
#---13---------------------------------- sig2stat <- function(x) {x %>% as.factor %>% as.numeric} stat2sig <- function(x) ifelse(x==1, -1, 1) #----14--correct----------------------------------- correct <- function(sig){ sig <- Hmisc::Lag(sig) %>% na.omit bal <- cumsum(sig * (price[ ,6] %>% tail(.,length(sig)))) ma <- pracma::movavg(bal, 16, "t") roc <- TTR::momentum(ma, 3)%>% na.omit dbal <- (bal - ma) %>% tail(., length(roc)) dbr <- (roc + dbal) %>% as.matrix() sig.cor <- sign(dbr) S <- sig.cor * tail(sig, length(sig.cor)) bal <- cumsum(S * (price[ ,6]%>% tail(.,length(S)))) K <- tail(bal, 1)/length(bal) * 10 ^ Dig Kmax <- max(bal)/which.max(bal) * 10 ^ Dig dd <- fTrading::maxDrawDown(bal) corr <<- list(sig.c = sig.cor, sig.res = S, bal = bal, Kmax = Kmax, K = K, dd = dd) return(corr) }
Чтобы получить вектор сигналов с предсказанием на 1 бар вперед, будем использовать пакет "markovchain" и функцию pred.sig().
#---15---markovchain---------------------------------- pred.sig <- function(sig, prev.bar = 10, nahead = 1){ require(markovchain) # Переведем наблюдаемые корректирующие сигналы в состояния stat <- sig2stat(sig) # Вычислим параметры модели # если модели еще нет в окружении if(!exists('MCbsp')){ MCbsp <<- markovchainFit(data = stat, method = "bootstrap", nboot = 10L, name="Bootstrap MС") } # Зададим необходимые константы newData <- tail(stat, prev.bar) pr <- predict(object = MCbsp$estimate, newdata = newData, n.ahead = nahead) # пристыкуем предсказанный сигнал к входному sig.pr <- c(sig, stat2sig(pr)) return(sig.pr = sig.pr) }
Теперь запишем расчет результирующего сигнала для выполнения экспертом в компактной форме:
sig <- resBal[[1]]$sig sig.cor <- correct(sig) sig.c <- sig.cor$sig.c pr.sig.cor <- pred.sig(sig.c) sig.pr <- pr.sig.cor$sig.pr # Результирующий вектор сигналов для эксперта S <- sig.pr * tail(sig, length(sig.pr))
- Сглаживание предсказанного сигнала.
#---16---smooth------------------------------------
smoooth <- function(sig){
# сгладим предсказанный сигнал
# определим параметры скрытой модели Маркова
# если модели еще нет в окружении
require(mhsmm)
if(!exists('obj.sm')){
obj.sm <<- sig2stat(sig)%>% smooth.discrete()
}
# сгладим сигнал полученной моделью
sig.s <- predict(obj.sm, x = sig2stat(sig))%>%
extract2(1)%>% stat2sig()
# вычислим баланс по сглаженному сигналу
sig.s1 <- Hmisc::Lag(sig.s) %>% na.omit
bal <- cumsum(sig.s1 * (price[ ,6]%>% tail(.,length(sig.s1))))
K <- tail(bal, 1)/length(bal) * 10 ^ Dig
Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
dd <- fTrading::maxDrawDown(bal)
return(list(sig = sig.s, bal = bal, Kmax = Kmax, K = K, dd = dd))
}
Вычислим и сравним баланс по предсказанному и сглаженному сигналам.
sig <- resBal[[1]]$sig sig.sm <- smoooth(sig) plot(sig.sm$bal, t="l") lines(resBal[[1]]$bal, col=2)
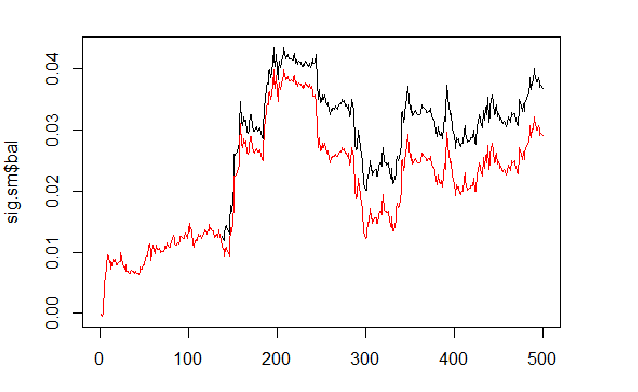
Рис.6 Баланс по сглаженному и предсказанному сигналам
Как видим, качество стало незначительно лучше, но просадка осталась. Этот способ мы не будем использовать в нашем эксперте.
sig.sm$dd $maxdrawdown [1] 0.02335 $from [1] 208 $to [1] 300
4. Структурная схема алгоритма эксперта
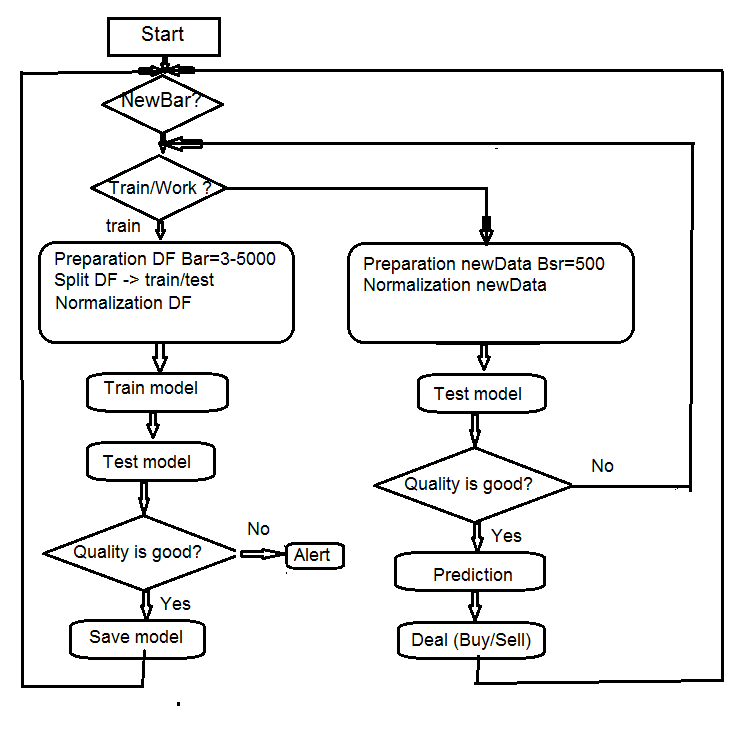
Рис.7 Структурная схема алгоритма эксперта
4.1. Описание работы эксперта
Поскольку работа эксперта происходит в двух потоках (mql и Rterm), опишем процесс их взаимодействия. Отдельно поговорим о том, какие операции выполняются в каждом из них.
4.1.1 MQL
После установки эксперта на график:
в функции init()
- проверяем настройки терминала (доступность DLL, разрешение торговать);
- устанавливаем таймер;
- запускаем Rterm;
- вычисляем и передаем в окружение R-процесса необходимые для работы константы;
- проверяем работает ли Rterm, если нет - алерт;
- выходим из init().
В функции deinit()
- останавливаем таймер;
- удаляем графические объекты;
- Останавливаем Rterm.
В функции onTimer()
- проверяем работает ли Rterm;
- если Rterm не занят и новый бар (LastTime != Time[0]):
- устанавливаем глубину истории в зависимости от того, первый это запуск эксперта или нет;
- формируем четыре вектора котировок (Open, High, Low, Close) и передаем их в Rterm;
- запускаем скрипт и уходим, не дожидаясь результата его исполнения;
- устанавливаем флаг get_sig = true;
- устанавливаем LastTime= Time[0].
- Иначе, если Rterm работает, не занят и флаг get_sig = true:
- определяем длину вектора sig, который мы должны получить от Rterm;
- приводим размер принимающего вектора в соответствие с размером источника. При несоблюдении Rпроцесс упадет;
- получаем последовательность сигналов (вектор);
- по последнему сигналу определяем, какую операцию необходимо выполнить (BUY, SELL, Nothing);
- если мы получили реальный сигнал, не ERR, сбрасываем флаг get_sig=false.
- далее стандартно:
- CheckForClose()
- CheckForOpen()
В этой своей части наш эксперт — "Исполнитель", выполняющий распоряжения, получаемые от "думающей" его части, отправляющий ордера, отслеживающий состояние открытых позиций и возможных ошибок при их открытии и выполняющий многие другие функции обычного эксперта.
4.1.2 Rterm
Исполняемый скрипт состоит из двух частей. Одна часть исполняется при первом входе, вторая — при последующих.
- если first:
- загружаем (при необходимости) нужные библиотеки из депозитария в интернете, инсталлируем их и загружаем в окружение Rterm;
- определяем необходимые функции;
- создаем матрицу котировок;
- подготавливаем набор данных для обучения и тестирования модели;
- создаем модель и обучаем модель;
- тестируем модель;
- вычисляем сигналы для исполнения;
- проверяем качество предсказания. Если оно больше или равно установленному минимуму — продолжаем. В обратном случае — передаем алерт.
- если !first:
- подготавливаем набор данных для тестирования и предсказания;
- тестируем модель на новых данных;
- вычисляем сигналы для исполнения;
- проверяем качество предсказания. Если оно если больше или равно установленному минимуму — продолжаем. В обратном случае — устанавливаем first = TRUE, т.е., требуем переучить модель.
4.2. Самоконтроль и Самообучение
Контроль качества предсказания сигналов моделью проводим, используя коэффициент К. Возможны два варианта определения границы допустимого качества. Первый — установить максимальное падение коэффициента отностительно максимального его значения. Т.е., если К < Kmax * 0.8, то следует переобучиться или остановить исполнение сигналов экспертом. Второй — установить минимальное значение К, при достижении которого нужно выполнить те же действия. В эксперте мы будем использовать второй метод.
5. Порядок установки и запуска
В приложении к статье представлены два эксперта: e_DNSAE.mq4 и e_DNRBM.mq4. Оба используют одинаковые наборы данных и практически одинаковый набор функций. Различие состоит в используемой модели глубокой сети. Первый использует DN, инициируемую SAE и пакет "deepnet". Описание пакета вы можете найти в предыдущей статье о глубоких нейросетях. Второй использует DN, инициируемую RBM и пакет "darch".
Раскладываем стандартно:
- *.mq4 в папку ~/MQL4/Expert
- *.mqh в папку ~/MQL4/Include
- *.dll в папку ~/MQL4/Libraries
- *.r в папку C:/RData
Поправляем путь к установленному языку R и к скриптам (как в mq4: #define так и в *.r: source() ).
При первом запуске эксперта он загрузит необходимые библиотеки из репозитория и установит их в окружение Rterm. Вы также можете предварительно инсталлировать их в соответствии с приложенным списком.
Как правило, R процесс "падает" именно из за отсутствия необходимых библиотек, неверно указанных путей к скриптам, и только в последнюю очередь — из за ошибок синтаксиса скрипта.
Отдельно приложен снимок сессии с исходными данными, который Вы можете открыть с помощью Rstudio и проверить все функции на работоспособность а также провести эксперименты.
6. Пути и методы улучшения качественных показателей.
Есть несколько направлений улучшения качественных показателей.
- оценка и выбор предикторов — применить генетический алгоритм оптимизации (ГА).
- определение оптимальных параметров предикторов и целевой переменной — ГА.
- определение оптимальных параметров нейросети — ГА.
Заключение
Проведенные эксперименты с пакетом "darch" показали следующие результаты.
- Глубокая нейросеть, инициируемая RBM, обучается хуже чем, с SAE. Для нас это не стало новостью.
- Сеть обучается быстро.
- Пакет имеет очень большой потенциал по улучшению качества предсказания, предоставляя доступ практически ко всем внутренним параметрам модели.
- Пакет позволяет использовать только нейросеть или только RBM с очень широким набором параметров, относительно других, стандартных.
- Пакет постоянно развивается, и в следующем релизе разработчик обещает дополнительные возможности.
- Обещанная разработчиками интеграция языка R с терминалом МТ4/МТ5 даст возможность трейдерам использовать новейшие алгоритмы без использования дополнительных DLL.
Приложение
- Сессия R процесса Sess_DNRBM_GBPUSD_30
- Архив с экспертом " e_DNRBM "
- Архив с экспертом " e_DNSAE"
 Графические интерфейсы III: Группы простых и многофункциональных кнопок (Глава 2)
Графические интерфейсы III: Группы простых и многофункциональных кнопок (Глава 2)
 Калькулятор сигналов
Калькулятор сигналов
 В MetaTrader 5 добавлена хеджинговая система учета позиций
В MetaTrader 5 добавлена хеджинговая система учета позиций
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Спасибо за ответ.
Отчего считаете бактесты бесполезными? Не совсем понимаю.
В синхронном режиме - вместо RExecuteAsync использовать RExcecute, и перенести код в OnTick. Могу приложить свою версию кода, работающую в тестере.
Среднее вознаграждение на бар это конечно хорошо, но его при тестировании также нет, около нуля(значение К в визуальном режиме):
Да я имел ввиду Accuracy. суть вопроса в том, что при казалось бы неплохой точности 0.74 нет прибыльности. Вот и спрашиваю, при какой точности у вас получается результат.
Сбросьте код , я посмотрю что не так. Можно в личку.
Удачи
Сбросьте код , я посмотрю что не так. Можно в личку.
Удачи
Вот код, там надо только пути проставить в R и MQL скриптах.
Задержусь с ответом. Много проблем с карантином.
Задержусь с ответом. Много проблем с карантином.
Как там дела с карантином?
Вот нашел, может пригодится: https://github.com/blue-yonder/tsfresh
https://arxiv.org/abs/1304.1209