Заблуждения, Часть 2: Статистика - лженаука, или Хроника пикирующего бутерброда

Введение

Первая часть названия статьи с несущественным изменением пунктуации – цитата из поста SergNF, 17.04.2008 14:04, https://www.mql5.com/ru/forum/108164. Да, самая строгая математика тоже может оказаться лженаукой в руках «исследователя», решившего поиграться красивыми формулами, не имеющими никакого практического применения.

Скепсис автора цитаты, даже смягченный тремя смайликами, все равно остается явным. Причины примерно понятны: многочисленные попытки применения методов статистики к объективной реальности, т.е. к финансовым рядам, разбиваются о скалы нестационарности процессов, «толстохвостости» сопутствующих вероятностных распределений и недостаточного объема финансовых данных. Ни одну из известных сейчас моделей рынка нельзя признать достаточно адекватной реальности. И даже если удается найти какие-то статистические закономерности, результаты их использования как будто оказываются не соразмерны тем усилиям, которые были затрачены на их выявление.

В данной публикации я попытаюсь обратиться не к финансовым рядам как таковым, а к их субъективному отражению – в данном случае к тому, как эти ряды пытается оседлать трейдер, т.е. к торговой системе. Выявление статистических закономерностей процесса, описывающего результаты сделок, оказывается довольно увлекательным занятием. В некоторых случаях возможно даже сделать вполне достоверные выводы о модели этого процесса и применить эти выводы к торговой системе.

Приношу извинения за уровень изложения тем читателям, которые далеки от математики, но, вероятно, это – неизбежное следствие самого содержимого статьи. Похоже на то, что обещание, данное в конце предыдущей статьи, мне не удалось выполнить. Итак, начнем наше исследование.

В предыдущей статье серии «Заблуждения» нам удалось сконструировать искусственный пример, наглядно показывающий, каким образом можно превратить стратегию, явно прибыльную при ММ «lot=0.1», в убыточную при геометрическом ММ. В примере использовалась очень регулярная последовательность прибыльных и убыточных сделок, которая «в природе» вряд ли встречается: П У П У П У П У П У П У… Самый первый вопрос таков: почему я рассматриваю именно такие «регулярные» последовательности?

Серии убытков: краткое касание вопроса

Причина проста и указана в статье Мой первый "грааль" (приведу более-менее законченную цитату):

Вместе с тем, никогда нельзя сказать наперёд как будут распределены убыточные ордера среди прибыльных. Это распределение в значительной степени носит случайный характер.

А. Идеальным случаем последовательности Прибылей и Убытков является равномерное их распределение на протяжении всей торговой истории:

П П П У П П П У П П П У П П П У П П П У П П П У П П П У...

Однако, нет никакой гарантии, что в реальной торговле распределение всегда будет идеальным. Как раз наоборот, существует большая вероятность, что рано или поздно встретится случай с длинной серией последовательных убытков.

В. Один из вероятных случаев неравномерного распределения прибыльных и убыточных торговых операций в реальной торговле:

П П П П П П П П П П П П П П П УУУУУ П П П У П П П У...

Здесь показана серия из 5 последовательных убытков, хотя не исключена возможность и более длинной серии потерь. (обратите внимание, что в данном случае отношение прибыльных и убыточных ордеров сохраняется в пределах 3 : 1 ).

Таким образом, «регулярное» чередование прибыльных и убыточных сделок идеально в смысле минимальных просадок (и максимального фактора восстановления RF). И, если удается показать (как это сделано в предыдущей статье для чередующихся прибыльной и убыточной сделок), что даже в этом идеальном случае при полученных значениях м.о. прибыльной и убыточной сделок система убыточна на геометрическом ММ, то она будет однозначно еще хуже при нерегулярном распределении сделок по их результатам.

Примечание: допустим, что соотношение прибыльных к убыточным сделкам (по их количествам) равно 14:9. Как следует распределить их по времени, чтобы добиться минимальных просадок? Задача не из простых, даже если рассматривать вариант ММ «lot=0.1» (если говорить о доказательстве оптимальности ее решения). Почти ясно, что нужно как можно более равномерно распределить убытки в серии – например, так:

П У П У П П У П П У П П У П У П У П П У П П У...

Это «элементарная серия», состоящая из 23 сделок, 14 из которых прибыльны. Далее эта серия повторяется. Интуитивно понятно, что эта серия имеет значительно меньшие просадки на обоих типах ММ, чем, скажем, вот такая:

П П П П П П П П П П П П П П У У У У У У У У У…

Особенно это заметно на геометрическом ММ – по соображениям, изложенным ранее. Однако и такая серия убытков (убыточный кластер) – не предел. Для понимания этого обстоятельства придется вспомнить основы теории вероятностей. Но перед этим договоримся о терминологии.

Терминология

В этой статье содержится много терминологии, связанной с сериями Бернулли, а также гистограмм, демонстрирующих различные вероятностные распределения. Дабы не путать котлеты с бифштексами, определимся с терминами. Итак:

1. Полная серия сделок в любом случае будет называться здесь просто серией. Это относится как к сериям, полученным при обработке результатов одиночного реального тестирования, так и к сериям, полученным синтетически, при генерации соответствующей серии Бернулли. Если нужно дополнительно указать и длину серии, будем указывать ее так – 3457-серия (серия из 3457 сделок).
2. Последовательность идущих подряд сделок одного знака внутри серии (прибыльных или убыточных – либо «успехов» или «неудач») здесь будет называться кластером. Если нужно также одновременно указать длину кластера, то он будет называться, например, 7-кластером (кластер длины 7).
3. Множество серий (обычно речь в этом контексте будет идти о синтетических сериях) назовем массивом серий. Уточнение, связанное с указанием количеств: 65000-массив 5049-серий (65000 серий Бернулли длиной каждая в 5049 сделок).
4. При построении гистограмм иногда придется учитывать кластеры не только внутри одной серии, но просматривать весь массив серий. Название гистограммы соответствует параметру, распределение которого мы строим. Вместо того, чтобы писать «Гистограмма распределения количества кластеров длины 4 в массиве из 5000 серий длиной 3174 сделки каждая», будем краткими: «4-кластеры в 5000-массиве 3174-серий».

Схема Бернулли: основы теории

Многие практические задачи, в которых рассматривается последовательность событий, часто можно свести к следующей схеме:

• Каждое событие имеет только два исхода – «успех» и «неудача». Вероятность успеха – p, неудачи – q=1-p.
• Вероятность исхода события не зависит от истории событий, предшествовавших ему.
  

Эта схема называется схемой Бернулли. Нашу закодированную цветную последовательность можно было бы считать схемой Бернулли, если бы мы были уверены во втором пункте схемы.

У автора есть серьезные основания считать, что для многих ТС так оно и есть. Вот косвенные доводы в пользу этой гипотезы:

• Информация о Z-счете системы, по отзывам тех, кто пытался применять ее для оптимизации ММ, оказывается бесполезной при попытках вычисления вероятности прибыльности конкретной сделки – даже если вероятность успеха (прибыльной сделки) более 90%;
• Эффективность разных схем мартингейла, судя по всему, также равна нулю и даже отрицательна, так как приводит к неприемлемым просадкам.

Поэтому в первом приближении было бы логично принять, что для подавляющего числа ТС серия из последовательных сделок удовлетворяет критериям схемы Бернулли. Эта гипотеза ведет к далеко идущим последствиям.

Классическая формула для вероятности k успешных исходов (которыми мы можем назвать и убыточные сделки, кстати!) в серии из n испытаний в схеме Бернулли такова (вероятность успеха равна p):

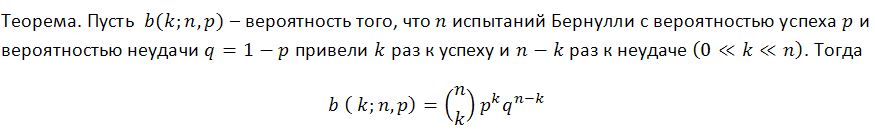
Эта формула дает представление о некоем интегральном параметре серии, количестве успехов, - но ничего не говорит о том, насколько неравномерно эти успехи распределены, т.е. о длине возможных кластеров. Исследование вопроса о вероятных убыточных кластерах в сериях Бернулли – гораздо более сложная задача, решение которой изложено у Феллера [1]. Ниже приведены формулы для матожидания длины серии испытаний и ее дисперсии при заданных параметрах p (вероятность успеха), q (вероятность неудачи), r (длина прибыльного кластера) – при условии, что мы имеем серию испытаний по схеме Бернулли: математическое ожидание и дисперсия времени возвращения для серии успехов длины r равны соответственно

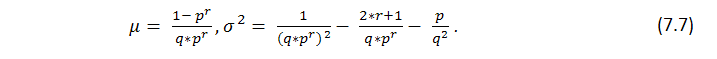
Из теоремы следует, что при больших n число серий длины r, полученных в n испытаниях, имеет приблизительно нормальное распределение, т.е. что при фиксированных вероятность неравенства

стремится к

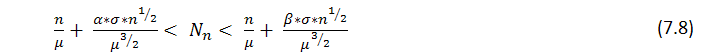
В таблице указаны математические ожидания для ряда типичных времен возвращения.

Длина серии, r	p = 0.6	p=0.5 (монета)	p=1/6 (кость)
5	30.7 сек.	1 мин.	2.6 часа
10	6.9 мин.	34.1 мин.	28.0 мес.
15	1.5 часа	18.2 часа	18 098 лет
20	19 часов	25.3 дня	140.7 млн. лет

Таблица 1. Среднее время возвращения для серии успехов, когда производится по одному испытанию в секунду.

Первое следствие: если теперь применить (7.7) к убыткам и выразить r из первой формулы, получим, что самый длинный кластер убытков в зависимости от длины серии испытаний не ограничен по длине, так как растет по закону логарифма! Особенно жесткий удар это следствие наносит по пипсовочным стратегиям (пояснения см. ниже) – в силу особенностей, присущих таким ТС.

Второе следствие: ограниченность, существенное замедление роста или, наоборот, существенное превышение максимальной длины кластера убытков в зависимости от длины серии испытаний могут намекать на то, что ТС не удовлетворяет схеме Бернулли. Например, если при заданных n, p, q реальный максимальный кластер убытков по длине равен 5, а вычисленная из гипотезы «схема Бернулли» - 15, то у нас появляются серьезные подозрения, что мы нашли небернуллиеву систему, т.к. результаты сделок вполне могут оказаться зависимыми событиями.

Третье следствие: если гипотеза «схема Бернулли» верна, то такая стратегия ничем не отличается от схемы бросания асимметричной монетки с вероятностями выпадения сторон p, q=1-p (или, проще, подбрасывания бутерброда, намазанного маслом).

А теперь посмотрим с этой точки зрения на пару «интересных» стратегий.

Пипсовка: Lucky, часть 1

Все или почти все пипсовочные ТС обладают рядом общих качеств:

• SL>>TP (типичные значения – 20 и 2);
• p >> q (вероятность прибыльной сделки – выше 80%, иногда и до 99%);
• количество сделок очень велико и на периоде 1 год может измеряться десятками тысяч.

Мы не будем распространяться на тему третьего пункта – о том, в каких ДЦ такое возможно, а в каких нет. Эта тема подробно раскрыта в упоминавшейся выше статье SK., а также на форуме. Будем считать, что ДЦ не мешает нашему герою реквотами, проскальзываниями, увеличенными уровнями MODE_STOPLEVEL и т.п.

Трейдер, создавший пипсовочную ТС, обычно пребывает в заблуждении по поводу частоты убыточных сделок. Корни этой иллюзии восходят к представлению о винеровости процесса цен закрытия и справедливости формулы Эйнштейна для броуновского движения: «если взять SL=20, TP=2, то вероятность того, что при движении цены от цены открытия сработает стоп-лосс, в (20/2)^2=100 раз ниже, чем вероятность того, что сработает тейк-профит; значит, такая ТС должна быть прибыльной». Иллюзорность этого представления заключается в том, что этот процесс не является винеровским, и соответствующие вероятности отличаются гораздо меньше, чем в 100 раз!

Далее, именно в этом случае гипотеза «схема Бернулли» вполне вероятна – просто потому, что чаще всего пипсовочные ТС пытаются играть на случайных особенностях процесса и его фильтрации, принятой в данном ДЦ.

А теперь возьмем параметры ТС, которая хорошо известна под именем Lucky (https://www.mql5.com/ru/code/7464). В своем оригинальном виде (там же, Lucky_исходник.mq4) советник несомненно оказывается всего лишь игрушкой, так как ДЦ, который позволял бы открывать в день в среднем не менее нескольких сотен сделок с м.о. прибыльной порядка одного-двух пунктов, вряд ли существует. Тем не менее возможно, слегка модифицировав код и ужесточив требования к тейк-профиту, получить иногда все еще приличные кривые баланса/эквити. Код модифицированного советника (с учетом ограничения на количество одновременно открытых ордеров, которое в данном случае равно 1; пояснения см. ниже) прикреплен в конце статьи.

Главное преимущество этого советника в том, что он делает огромное количество сделок и дает богатый материал для статистики, в чем мы убедимся чуть ниже. Сейчас мы преследуем единственную цель: найти свидетельства, которые подтвердят или опровергнут гипотезу о том, что результаты сделок подчиняются схеме Бернулли. Для любителей поспорить о неслучайности рыночных движений специально уточню: я не подвергаю сомнению, что движения котировок далеко не всегда случайны. Я не собираюсь уподоблять рынок (именно рынок!) бросанию монетки а ля Башелье; меня здесь интересует только и именно статистика результатов сделок – и ничего больше. В нижеприведенных тестах некоторые наборы внешних параметров советников намеренно выбраны «сливными» - всего лишь для проверки приемлемости выдвигаемой гипотезы.

Итак, результаты первого теста:

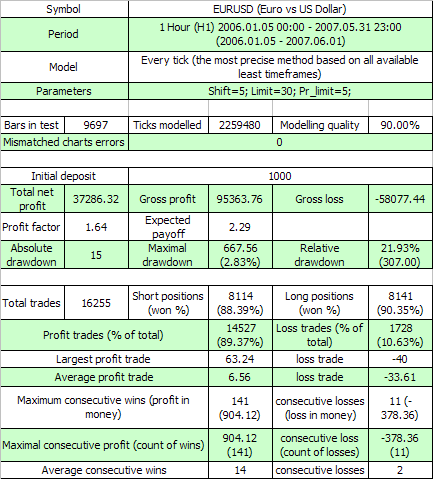
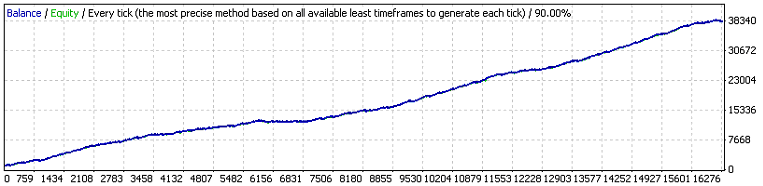
Обе первые внешние переменные имеют тот же смысл, что и в оригинальном коде, а третья – это значение прибыли в пунктах, которое ордер должен превысить, чтобы завершиться тейк-профитом. Оценим согласно (7.7) м.о. минимальной серии испытаний, необходимой для того, чтобы в ней встретился 11-кластер убытков (p=0.8937, q=0.1063, r_loss=11):

N_loss = 1 / (p * q^r_loss) – 1 / p ~ 57 140 275 804

Вот аналогичная оценка для м.о. длины серии испытаний, необходимой для появления в ней прибыльного 141-кластера:

N_profit = 1 / (q * p^r_profit) – 1 / q ~ 71 685 085

Мда-а… Как мы знаем, реальная длина серии испытаний равна всего 16255 сделкам, а не десяткам миллиардов или даже миллионов. Такое огромное превышение м.о. над реальной длиной серии может говорить только о том, что для данной ТС схема Бернулли напрямую вряд ли работает. Может быть, здесь вмешался какой-то фактор, который мы не учли?

Схема Бернулли: любопытный результат

Такой фактор есть: советник может одновременно открыть гораздо больше одной сделки: на второй сотне (ордеры 158…163) он открыл целых 6 сделок подряд (и закрывает он их, кстати, тоже «пачками»)! Этот «фактор мультипликации», вероятно, отвечает за значительно увеличенные длины кластеров в сравнении с ожидаемыми: если на рынке энергичный флэт с приличным объемом, то советник начинает открывать много сделок чуть ли не на каждом тике, но, так как он работает «на отбой», то в силу флэтового характера рынка и небольшого размера тейк-профита в сравнении со стоп-лоссом большинство их них, если не все, он закроет с прибылью. С другой стороны, если началось сильное направленное движение, советник начнет открывать однонаправленные сделки в направлении, противоположном рыночному движению, – и в конце концов значительную их часть он закроет с убытком и также «массированно».

Проведем простейшие арифметические выкладки. Возьмем снова обе формулы для м.о. длины полной серии испытаний из предыдущего параграфа. Здесь r_loss_real, r_profit_real – реальные длины максимальных соответственно убыточного и прибыльного кластера. Так как получаемые при этом числа N_xxxx весьма велики, то отбрасывание вторых членов практически не внесет ошибки, если мы поделим эти равенства друг на друга почленно:

N_loss / N_profit = (q * p^r_profit_real) / p * q^r_loss_real = p^(r_profit_real – 1)/ q^(r_loss_real – 1)

Логарифмируем и упрощаем:

ln(N_loss / N_profit) = (r_profit_real – 1) * ln(p) - (r_loss_real – 1) * ln(q)

Теперь отметим, что если испытания подчиняются схеме Бернулли, а длины самых длинных кластеров и обе вероятности p и q не слишком малы, то величины N_loss и N_profit при заданных реальных r должны быть примерно равны. Отсюда получаем любопытное примерное соотношение:

(r_profit_real – 1) / (r_loss_real – 1) * ln(p) / ln(q) ~ 1 (*)

Интересно, что если переписать его же иначе:

p^(r_profit_real – 1) ~ q^(r_loss_real – 1)

то тут же проясняется смысл соотношения (*): в бернуллиевой ТС (при достаточно большой длине серии испытаний и не малых вероятностях p и q ) вероятности двух максимально длинных кластеров («успехов» и «неудач») примерно равны. На самом деле этот принцип применим и к другим ТС, не являющимся бернуллиевыми, но сама форма соотношения (*) специфична именно для схемы Бернулли. Это соотношение можно считать грубым тестом ТС на бернуллиевость.

Пипсовка: Lucky, часть 2

Исключаем фактор мультипликации: вводим ограничение на число одновременно открытых ордеров, равное 1. Так как количество ордеров на том же промежутке времени снижается в несколько раз, то мы расширим диапазон тестирования – с 1 января 2004 г. до 4 апреля 2008. Ниже приведена таблица результатов и некоторых расчетов (СБ – сокращение для «схемы Бернулли» – см. анализ ниже; первый «+» означает хорошее соответствие схеме Бернулли для прибыльных кластеров, второй – для кластеров убытков, «-» - отвергнутая гипотеза о СБ, «0» - сомнения в ее справедливости):

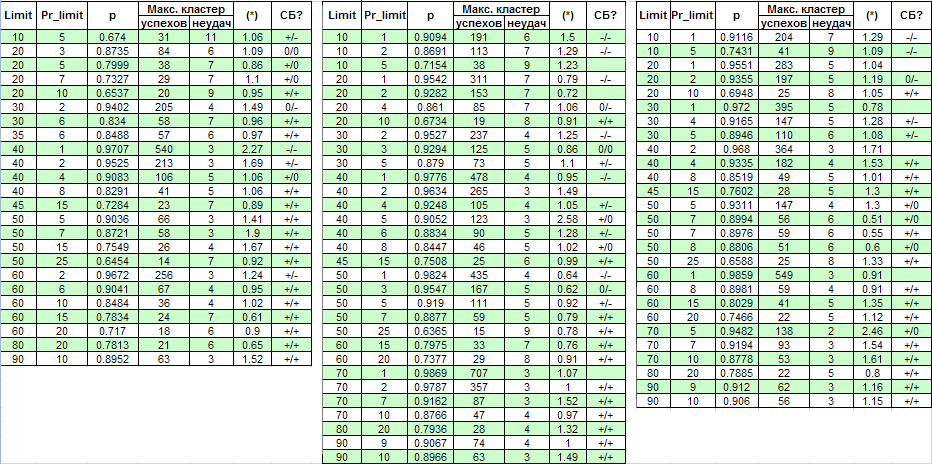
Автор приносит извинения за слишком большой размер таблицы – но это только для полноты картины. Выясняется, что параметр (*) недостаточен для суждения о бернуллиевости системы, т.к. иногда, даже когда он близок к 1, систему трудно сразу отнести к бернуллиевой.

Критерий соответствия ТС схеме Бернулли. Описание работы скрипта

Каким образом можно более достоверно разбить результаты тестирований на две группы – схемы Бернулли и «не-схемы Бернулли»? Можно попытаться сделать это несколькими способами, но вот, на мой взгляд, самый простой из них: если генерировать много серий Бернулли с параметрами, соответствующими реально обнаруженным при тестировании, то в случае бернуллиевости ТС функция распределения длин кластеров должна остаться примерно неизменной. Этот факт очевидно вытекает из предположения о постоянстве вероятности успеха и о независимости сделок.

К сожалению, теоретическая функция распределения кластеров удач/неудач по их длине мне не известна. Выше я приводил формулы, позволяющие оценить м.о. количества кластеров удач в серии испытаний в зависимости от ее длины и вероятности успеха (см. (7.8) выше). Для этого у Феллера ([1]) есть специальная методика, вытекающая из теории рекуррентных событий, к каковым подобные кластеры и относятся. Эта методика на первый взгляд не слишком соответствует трейдерскому пониманию термина «серия удач», но такая ее модификация значительно упрощает саму теорию, чтобы идентификация события «регистрация r-кластера» не зависела от будущего ([1], стр. 302):

Серии успехов в испытаниях Бернулли. Термин "серия успехов длины r" был определен различными способами. Вопрос о том, считать что ряд из трех последовательных успехов содержит 0, 1 или 2 серии длины 2 является в значительно степени вопросом соглашения и удобства, и для разных целей мы принимали разные определения. Однако, если мы хотим применять теорию рекуррентых событий, то понятие серии длины r нужно определить так, чтобы после завершения серии процесс каждый раз начинался снова. Это значит, что мы должны принять следующее определение: Последовательность n букв У и Н содержит столько серий успехов длины r, сколько в ней имеется неперекрывающихся подпоследовательностей, каждая из которых состоит ровно из r стоящих рядом букв У. Если в последовательности испытаний Бернулли в результате n-го испытания прибавляется новая серия, то мы будем говорить, что эта серия появляется при испытании с номером n.

Так, в последовательности УУУ|УН|УУУ|УУУ имеется три серии длины 3, появившиеся при 3, 8 и 11 испытаниях; в той же последовательности содержится пять серий длины 2 и они появляются при 2, 4, 7, 9 и 11 испытаниях.Это определение значительно упрощает теорию, так как серии фиксированной длины становятся рекуррентыми событиями. Оно равносильно подсчету последовательностей, образованных по меньшей мере r следующими друг за другом успехами, с той оговоркой, что 2r
последовательных успехов считаются за две серии и т.д.

С другой стороны, для трейдера количества кластеров успехов ("серий успехов" по Феллеру) в указанном ряду (УУУУНУУУУУУ) будут следующими: вначале 4-кластер успехов, а затем, после одной неудачи, 6-кластер успехов. Никаких завершенных кластеров длины 1, 2, 3 и 5 для трейдера нет, хотя по Феллеру есть. Этот пассаж из [1] приведен здесь только для того, чтобы обозначить сложность проблемы. Таким образом, мы просто генерируем довольно большое количество серий Бернулли и сразу выявляем в них серии, соответствующие пониманию их трейдером (15 успехов подряд, после этого завершающихся неудачей, – это не 15 регистраций 1-кластеров или 5 регистраций 3-кластеров, как по Феллеру, а только одна регистрация «истинного» 15-кластера). Для целей проверки серии на бернуллиевость достаточно 1000 серий Бернулли.

По этой идее был написан скрипт, позволяющий загрузить последовательность результатов реальных сделок в массив, после чего получить данные для построения гистограммы распределения количеств кластеров разной длины в массиве серий. В этом же скрипте есть функции, позволяющие генерировать серии Бернулли и подготавливать результаты для построения гистограмм в MS Excel. Мне не хотелось бы вставлять код скрипта в текст статьи; вместо этого я просто дам общие комментарии по коду. Сам скрипт приложен в конце статьи. Файл отчета тестера должен предварительно быть в каталоге experts\files\Sequences\, а его имя вынесено во внешние параметры скрипта.

Вначале на основе файла отчета тестера с помощью функции readIntoArray() бинарные результаты сделок (1 или -1) вносятся в глобальный массив _res[]. Для понимания работы будем иллюстрировать наши пояснения с помощью небольшого массива. В результате работы этой функции образуется, например, такой массив _res[] (число сделок, т.е. длина серии - 50):

1,1,-1,-1,1,1,1,1,1,-1,1,1,1,1,1,1,1,-1,1,1,-1,-1,-1,-1,1,1,1,-1,1,1,1,1,-1,1,-1,1,-1,-1,-1,1, 1,-1,1,1,1,1,1,1,1,1

Затем функция formClustersArray( int results[], int& sequences[], int& h, int nr ) подсчитывает длины кластеров и в зависимости от глобального параметра _what, определяющего, что нас интересует – прибыли или убытки, записывает длины нужных нам серий в массив sequences[] (на самом деле - в глобальный массив _seq[]). Подсчитаем кластеры в этом массиве:

2,-2,5,-1,7,-1,2,-4,3,-1,4,-1,1,-1,1,-3,2,-1,8

Отрицательными выписаны обозначения кластеров убытков. Понятно, что сумма модулей всех чисел равна длине серии, т.е. 50. Допустим, нас интересуют убытки, т.е. _what = -1. Тогда в массиве _seq[] будут храниться только отрицательные числа, но со знаком "плюс":

2,1,1,4,1,1,1,3,1

После этого массив _seq[] обрабатывается с целью построения массива _histogramReal[]. Достаточно теперь подсчитать количества 1-, 2-, 3- и т.п. кластеров и по порядку записать их в массив. В результате в массиве _histogramReal[] будут следующие числа:

6,1,1,1

Это означает, что в нашей серии имеется 6 убыточных 1-кластеров, 1 убыточный 2-кластер, 1 убыточный 3-кластер и 1 убыточный 4-кластер. Далее последний массив в виде длинной строки с его значениями, разделенными запятыми, записывается в выходной файл. Файл не закрывается, т.к. надо записать в него еще аналогичные «гистограммы» синтетических серий испытаний по схеме Бернулли.

При формировании «синтетик» ключевой функцией является генератор одиночного испытания по схеме Бернулли. Несмотря на столь простой код, работает очень неплохо: никаких «краевых эффектов», ответственных за искажение равномерного распределения результатов на отрезке [0, 32767], не отмечено.

// генерирует одиночное испытание Бернулли (+-1 с разными вероятностями)
int genBernTest( double probab )
{
   int rnd = MathRand();
   if( rnd < probab * 32767 ) return(  _what );
   else                       return( -_what );
}

Эта функция после единичного вызова MathSrand( GetTickCount() ) вызывается в цикле столько раз, сколько реальных сделок было у нас на отрезке тестирования (_testsTotal), после чего ее результаты аналогично обрабатываются функциями подсчета кластеров и формирования «гистограммы». Эти действия отвечают за создание одной гистограммы, соответствующей одиночному тестированию (функция genSynthHistogr( int& h, int nr ) ). И, наконец, последняя функция вызывается в цикле, чтобы в результате генерировать массив серий Бернулли, сформировать по ним гистограммы и записать их в выходной файл.

Теперь этот файл можно открывать в MS Excel, строить нужные нам диаграммы и делать выводы о соответствии системы схеме Бернулли. Числа в строках файла имеют следующий смысл (табличка обрезана справа начиная с 5-кластеров):

№№ серии испытаний	Длина макс. кластера	Число 1-кластеров	Число 2-кластеров	Число 3-кластеров	Число 4-кластеров
1	9	1639	1058	724	440
0	11	1649	1044	688	478
1	8	1681	1093	675	458
2	13	1628	1067	701	461
3	7	1616	1039	726	474
4	12	1601	1054	699	465

Отметим, что первая строка файла – это результаты реального тестирования, а строки ниже соответствуют синтетическим сериям испытаний с номером начиная с нулевого.

И, наконец, последний этап - собственно оценивание результатов реального тестирования по соответствию схеме Бернулли: из синтетических серий Бернулли выбираются соответствующие столбцы, чтобы по ним составить гистограммы количества кластеров нужной длины. Например, чтобы составить гистограмму распределения количества прибыльных 1-кластеров, нужно взять 3-й столбец (1649, 1681, 1628, 1616, 1601….); общее количество таких чисел равно числу синтетических серий Бернулли). Для прибыльных 2-кластеров – четвертый столбец (1044, 1093, 1067, 1039, 1054…) и т.п.

Такие гистограммы строятся согласно методике, описанной у Булашева [7], после чего проверяется нулевая гипотеза о равенстве цифры в реальном тесте оценке среднего исходя из синтетик - при принятом заранее уровне значимости, равном 0.05 (примерно два стандартных отклонения).

Первые результаты

Запустим скрипт на результатах тестирования эксперта Lucky при параметрах 3, 20, 10. Параметры скрипта: _what = 1 (прибыльные кластеры), _globalSeriesQty = 5000. Параметр (*) в большой таблице близок к 1, т.е. можно ожидать, что результаты работы скрипта должны показать нам соответствие схеме Бернулли. Приводим записи в файле, соответствующие непосредственной проверке нулевой гипотезы, для длин кластеров 1-6 (они слегка причесаны к табличной форме для улучшения их восприятия):

// Первая строка файла (реальный тест). Первые две цифры - это номер серии и длина максимального кластера.

1,20,1639,1058,724,440,271,212,137,91,62,30,26,22,5,7,1,4,1,0,1,1,

…

// Конец файла (частично):

В каждой из 6 двухстрочных таблиц верхняя строка соответствует левым границам интервалов гистограмм, а нижняя - количеству серий Бернулли (из 5000), в которых количества кластеров соответствующей длины попали в эти интервалы. Ниже то же самое показано в графическом виде (число прибыльных r-кластеров в сериях Бернулли при общем количестве серий, равном 5000):

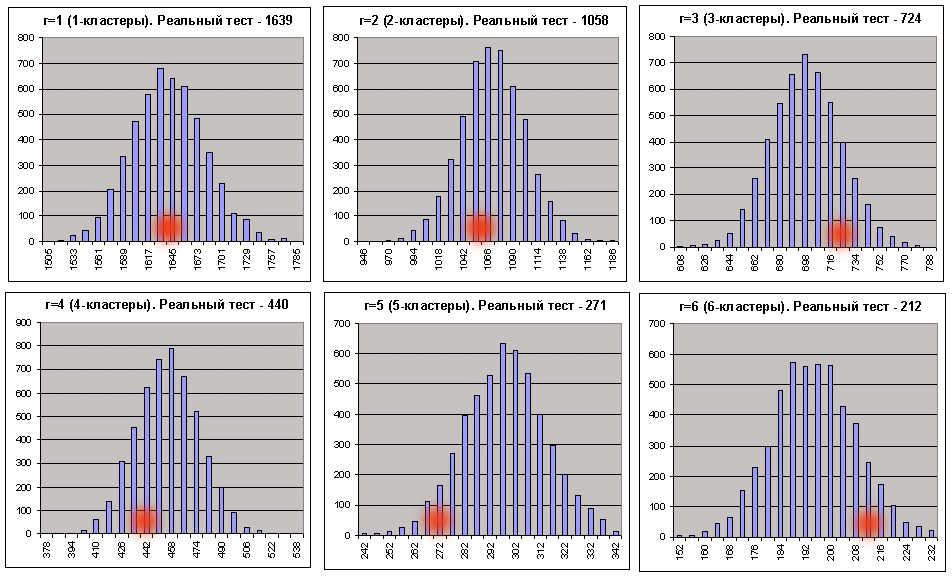
Абсциссы красных размытых пятен соответствуют количествам кластеров, полученным в реальном тесте. Тот же скрипт для кластеров убытков (_what = -1) при тех же параметрах выдает также очень неплохую картинку – со скидкой на разумную длину убыточных кластеров: как только число интервалов, вычисляемое согласно рекомендациям в [7], начинает превышать разброс данных в синтетиках, построение гистограммы с заданным количеством интервалов представляется невозможным. Тем не менее формальные нули в отчете скрипта не должны вас пугать, так как все нужные параметры можно вычислить и без гистограммы. При данных параметрах только на 3- и 7-кластерах убытков нулевая гипотеза была отвергнута.

В качестве решающего критерия, позволяющего отнести тестируемую систему к бернуллиевой, был избран весьма сомнительный критерий типа fuzzy. Рассмотрим принцип принятия решения на примере результатов работы скрипта с кластерами убытков:

Отличие реального теста от оценки среднего = -0.37 с.к.о.

Отличие реального теста от оценки среднего = 0.95 с.к.о.

Отличие реального теста от оценки среднего = -2.04 с.к.о.

Отличие реального теста от оценки среднего = -0.45 с.к.о.

Отличие реального теста от оценки среднего = 0.36 с.к.о.

Отличие реального теста от оценки среднего = 1.13 с.к.о.

Отличие реального теста от оценки среднего = 3.27 с.к.о.

Отличие реального теста от оценки среднего = 0.11 с.к.о.

Отличие реального теста от оценки среднего = 0.46 с.к.о.

Отличие реального теста от оценки среднего = -0.47 с.к.о.

Итак, формулировка решающего критерия:

• Если среднее модулей чисел не превышает 1.5 (здесь – 0.96),
• среднее чисел – не более 1.2 по модулю,
• число аутлаеров (здесь они выделены жирным шрифтом и соответствуют отличию, превышающему 2 с.к.о.) не превышает 20% от общего их числа,

то система считается «уверенно бернуллиевой». Если соответствующие граничные цифры – 2, 1.5 и 30%, то система «сомнительно бернуллиева». Если же цифры выходят за эти пределы в большую сторону, то гипотеза о соответствии системы схеме Бернулли отвергается. Считаю второй пункт целесообразным, так как отклонения не должны быть в-основном одного знака.

Мне не известны четкие статистические критерии соответствия испытаний схеме Бернулли, и поэтому пришлось придумывать критерий «на лету». Результаты этого импровизированного решающего критерия также приводятся в файле отчета о работе скрипта. Заинтересованный читатель может предложить более разумный решающий критерий.

В данном случае мы можем уверенно заключить, что система Lucky_ с параметрами 3, 20, 10 действительно подчиняется схеме Бернулли, т.е. схеме случайного бросания бутерброда с маслом.

Теперь возьмем один из самых худших случаев таблицы и выполним те же расчеты при числе серий Бернулли, равном 1000; параметры Lucky – 5, 10, 1. Рассмотрим прибыльные 1-кластеры:

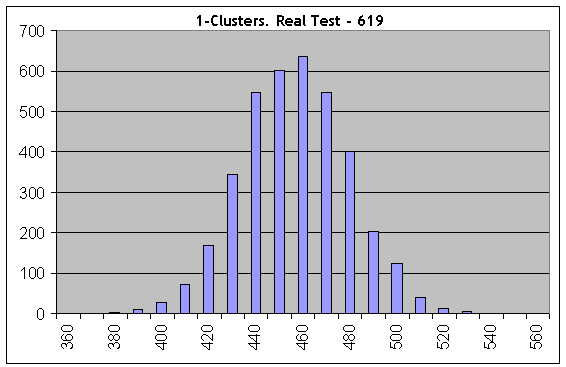
Уже на первой гистограмме все совсем иначе: результаты реального теста (619 1-кластеров) явно не вписались в «синтетики» с той же длиной серии испытаний и той же вероятностью успеха. Следовательно, сделки не являются независимыми.

Отметим, что аналогичные оценочные тесты с большинством остальных наборов параметров большой таблицы позволяют сделать вывод, что схема Бернулли («подбрасывание бутерброда с маслом») – скорее правило, чем исключение. Кроме того, встречаются такие случаи, когда по одному исходу сделки (например, прибыльным сделкам) схема Бернулли удовлетворяется, а по другому – нет. Это не мешает воспользоваться этой моделью хотя бы частично для получения ценной информации, о которой мы поговорим позднее в этой же статье. И последнее: решающий критерий не настолько надежен для убыточных кластеров в силу недостаточного объема статданных, но я прогнал скрипт и на них – просто для полноты картины.

Система Universum: снова схема Бернулли!

Теперь для исследования возьмем совершенно другую систему – Universum, исходный код которой находится по адресу https://www.mql5.com/ru/code/7999. По утверждению автора, система работает по сформированным барам, поэтому тестирование по всем тикам не требуется. Начальный баланс, при котором система успевает набрать статистику сделок на участке с 2000.01.01 по 2008.04.04, я установил равным примерно $10M. Первый открываемый лот – 0.1. Фактически изменяются три параметра – p, tp, sl. Эффекта мультипликации здесь нет, что упрощает исследование:

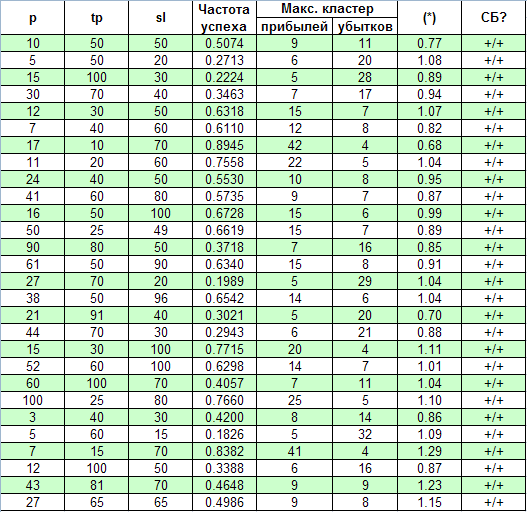
Здесь, как видим, согласие с параметром (*) значительно лучше, чем в предыдущем случае: значения (*) очень мало отличаются от единицы. Проверка с помощью решающего критерия также показывает, что во всех случаях, при довольно широком диапазоне параметров, эта ТС удовлетворяет схеме Бернулли.

Предварительные выводы

Ральф Винс в [4] предлагает другую процедуру проверки серии испытаний на соответствие схеме Бернулли. Это вычисление Z-score и тест результатов сделок на сериальную корреляцию (автокорреляцию исходного ряда и ряда, сдвинутого на единицу). У меня не создалось впечатления, что его процедура дает гораздо более значимые результаты, чем процедура, описанная здесь выше (проверка отклонения количеств кластеров разной длины в реальном тесте от модельных тестов). Да, предложенный решающий критерий весьма произволен и требует обоснования. Кроме того, как я отметил выше, надежность этой проверки при малой длине максимального кластера невысока (для Lucky_ это обычно тесты серий убытков). Однако, на мой взгляд, хотя этот решающий критерий и требует более значительных вычислений, он более полно охватывает специфику серий испытаний в контексте соответствия их схеме Бернулли. Этот вопрос требует дальнейших исследований, и он, конечно, не закрыт.

Тем не менее ожидания вполне оправдались: в большинстве случаев, при довольно сильно различающихся наборах внешних параметров, серии сделок соответствуют схеме Бернулли, а отклонения почти всегда вызваны систематической эксплуатацией закономерностей, присущих процессу фильтрования котировок у поставщика и чаще присущи системам с очень малым значением Pr_limit. Это особенно явно видно в большой таблице с результатами проверки Lucky_.

Винс в [4] отмечает, что серия, продемонстрировавшая при эмпирической проверке сериальной корреляции или Z-score зависимость между сделками, субоптимальна, и выявленную зависимость следует явно включить в ТС, чтобы добиться ее снижения по результатам тестов и повышения оптимальности ТС. Таким образом, отвлекаясь от результатов тестирования двух систем, следует определенно признать, что система Universum в целом значительно оптимальнее системы Lucky. Это, однако, совершенно не оправдывает ММ, применяемый в Universum.

О возможном применении факта бернуллиевости системы

1. Что мы теперь знаем?

Зная заранее, что хотя бы в некоторых случаях последовательность результатов сделок, выраженных числами 1 («успех», т.е. прибыль) и -1 («неудача», т.е. убыток), бернуллиева, мы получаем адекватную модель этого процесса. Теперь мы знаем об этом процессе совсем немало, так как фактически он является модификацией обычного броуновского движения со сносом. П. Самуэльсон ввел в финансовую теорию и практику геометрическое (или, как он говорил, - экономическое) броуновское движение ([6]):

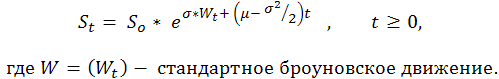
Таким образом, к кривой изменения баланса счета можно прямо применить весьма мощные результаты теоретического исследования стандартного броуновского движения (законы арксинуса, например). Однако теория броуновского движения весьма непроста и может быть понятна только «кругу ограниченных лиц» с солидной математической подготовкой в области стохастического интегрирования.

Второй подход заключается в отказе от высоких теоретических выкладок, прямой программной генерации продолжительных серий Бернулли и преобразовании их в кривые изменения баланса счета при «тестировании» на 0.1 лота. Для этого достаточно знать только средние значения прибыльной и убыточной сделки, а также частоту успеха p. Уже несколько сотен таких серий (1000-массив серий Бернулли, например) способны дать очень неплохое представление о том, на что способна стратегия, подчиняющаяся схеме Бернулли.

Важно четко сознавать, что такое синтетическое тестирование – неплохая альтернатива утомительному тестированию «по Пардо» ([5]): при предварительном обосновании ее применимости (гипотеза «последовательность сделок бернуллиева» не отвергается) она может принести нам немало информации о системе, существенно отличной от той, которую несет форвард-анализ, описанный в [5]. Разумеется, кривые баланса счета могут очень существенно отличаться от кривой, полученной по результатам реального тестирования.

В принципе никаких препятствий в реализации такого подхода у нас нет, так как такое тестирование выполняется на компьютере за несколько минут, а в результате мы получаем обширную информацию, которую можем тщательно проанализировать. К сожалению, объем статьи не позволяет выложить результаты здесь во всей полноте, но несколько графиков для Lucky_ с параметрами 4, 70, 10 на том же участке тестирования, что и в таблице, приведены ниже. Задача генерации синтетических серий Бернулли значительно проще, чем задачи, выполняемые вышеприведенным скриптом, и поэтому вполне достаточно средств MS Excel.

Реальное тестирование на 0.1:

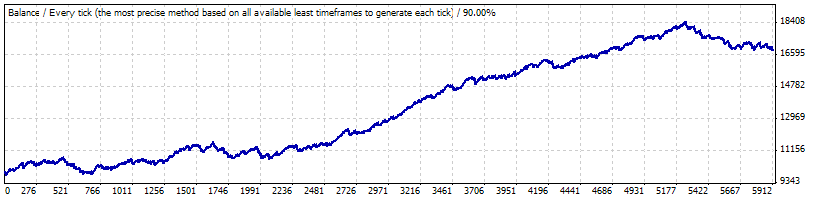
Нам важны следующие параметры из отчета, которые мы установим при генерации серий Бернулли и преобразовании серий в кривые изменения баланса счета:

Частота прибыльных сделок (p)	0.8765
Средняя прибыльная сделка	11.71
Средняя убыточная сделка	-73.73
Полное количество сделок	5904

Синтетические кривые изменения баланса на основе серий Бернулли:

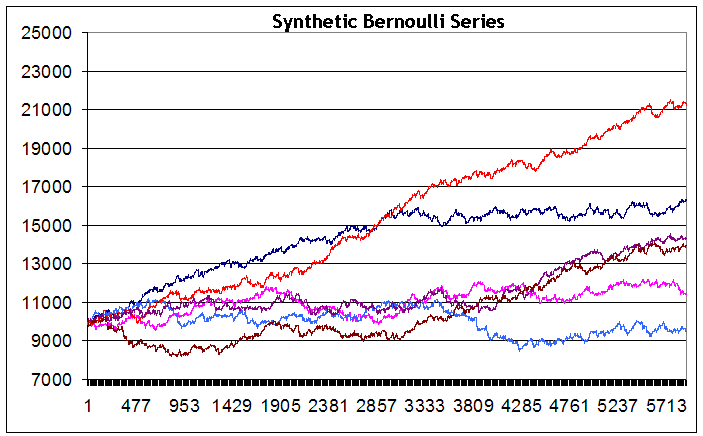
Как видим, несмотря на то, что серии генерировались при идентичных входных данных, интегральный результат баланса в конце периода тестирования существенно разнится от серии к серии – от небольшого убытка (голубая линия) до большой прибыли (красная линия). Признаюсь, дабы у читателя не создалось впечатление о крайней предвзятости этого исследования: мне так и не удалось генерировать серию с откровенно падающим балансом счета (хотя я очень этого хотел и сделал ради этого примерно 200 попыток, чтобы с чувством выполненного долга поставить на этой стратегии большой жирный крест). Возможно, при большем количестве серий это удалось бы сделать, но похоже на то, что такой случай именно для этой стратегии нетипичен. Кроме того, ни в одной из генерируемых серий я не увидел просадку, превышающую 2500 пунктов.

Рассмотрим теперь пару изолированных результатов, связанных с оценкой некоторых параметров стратегии, подчиняющейся схеме Бернулли.

2. Оценка максимального убыточного кластера, превышающего отчетные цифры («черного лебедя»)

Убедившись в бернуллиевости ТС, мы можем очень реалистично оценить максимальную длину убыточного кластера, который может поджидать нас при том же количестве сделок, которое было при реальном тестировании. Для этого достаточно генерировать много серий Бернулли и затем оценить наши шансы реального «черного лебедя» (см. [2, 3]), т.е. события, вероятность которого мы никак не смогли бы оценить на основании одних только результатов тестирования, так как на тестовом участке его просто не было. Именно благодаря теоретико-вероятностной модели мы получаем возможность набрать так необходимую нам статистику в любом количестве, какое нам захочется.

В качестве пробы пера воспользуемся результатами тестирования все той же системы Luсky_ при параметрах 4, 50, 7:

Согласно отчету, длина максимального кластера убытков равна 5. Теперь натравливаем на отчет тестера наш скрипт с очень большим количеством серий Бернулли, равным 65000, и параметром _what = -1 (кластеры убытков). Находим в отчете скрипта максимально длинную строчку (количества кластеров - начиная с третьей цифры):

26001 9 1030 136 13 4 0 0 0 0 1

Как видим, длина максимального кластера убытков может быть гораздо больше 5 (здесь – 9). Может быть, это слишком редкое явление? Да, очень редкое: на 65 тысяч серий испытаний оно встретилось лишь в одной серии, так что вероятность его осуществимости в реальном тесте с учетом гипотезы эргодичности можно считать практически исчезающей. Тем не менее эта оценка частоты слишком ненадежна, и полагаться на нее, естественно, нельзя: такая серия вполне могла бы встретиться и в количестве серий Бернулли, равном 20. В результате мы могли бы ошибочно, не зная статистических критериев оценки надежности, приписать этой оценке слишком большую вероятность.

Гипотеза эргодичности в варианте, предлагаемом мной, звучит так: вероятность события в пространстве синтетических тестов на основе адекватной модели явления примерно равна вероятности того же события во временном пространстве, т.е. при реальной торговле, – при условии, что количества сделок при реальном тестировании и в модельных тестах совпадают. Разумеется, предполагается, что последовательность результатов сделок в реальном тесте, как и в схеме Бернулли, стационарна во времени. При большом количестве сделок это утверждение не столь далеко от реальности, так как единственным источником нестационарности может, по-видимому, служить только «дрейф удачи», распределенный по нормальному закону и рассмотренный ниже.

Ниже приведена таблица количеств кластеров убытков в 65000-массиве серий Бернулли:

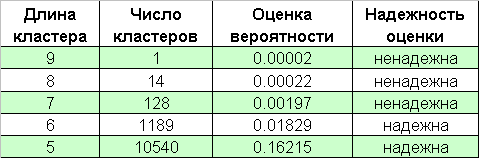
Все же следует помнить и о «черных лебедях», которые приходят именно тогда, когда их менее всего ждешь.

Противовесом приведенным выкладкам могут служить оценки для «черных лебедей» противоположного характера – прибыльных кластеров увеличенной длины. Мы помним, что тест на реальных данных показывает, что максимальная длина прибыльного кластера равна 59. Прогнав аналогичный тест при 65 000 серий испытаний, снова найдем самую длинную строку в отчете скрипта:

44118 153 115 117 111 87 70 71 52 51 50 40 36 42 42 34 20 32 15 20 20 13 10 11 12 8 5 7 3 5 4 2 2 6 7 0 2 1 2 1 1 5 0 0 1 0 0 0 0 0 0 1 0 0 2 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1

Это серия испытаний под номером 44118, с длиной максимального прибыльного кластера, равной 153 сделкам (2-е число в списке), – примерно в 2.6 раза больше, чем максимальный прибыльный кластер в тесте на реальных данных! Однако статистически значимые оценки частот кластеров получаются при их длинах примерно от 80 (оценка вероятности серии – 0.0088) и ниже, а число 80 все же значительно выше числа 59. При этом квантиль порядка ½ (значение длины кластера, при которой интегральная функция распределения принимает значение 0.5, т.е. такое, которым само распределение делится на две равные части по площади под функцией распределения плотности вероятности) для прибыльных кластеров составляет примерно 62, т.е. чуть больше 59. Гистограмма распределения длины максимального кластера по массиву серий Бернулли приведена ниже для справки:

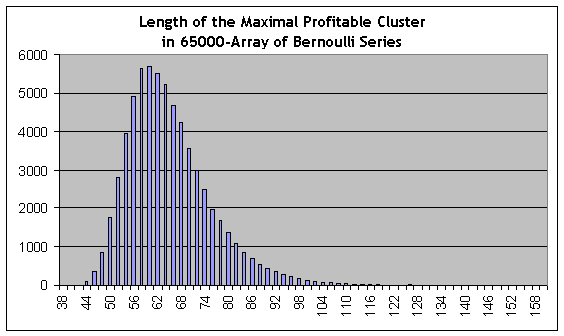
Конечно, термин «черный лебедь» употреблен здесь не слишком аккуратно, так как согласно Талебу это, судя по всему, – событие, вероятность которого невычислима. Тем не менее скромно отметим, что, руководствуясь одними только эмпирическими данными (отчет тестирования) и не привлекая никаких теоретических моделей, было бы трудно сделать статистически достоверные выводы о вероятности убыточных 6-кластеров или прибыльных 80-кластеров – т.е. того, чего в отчете нет!

3. «Дрейф неудачи»: неблагоприятное отклонение вероятности неудачи от эмпирической частоты. Подход к снаряду № 1

При большом количестве испытаний в серии по схеме Бернулли (порядка нескольких тысяч) частота неудачи f мало отличается от вероятности неудачи q и подчиняется «правильному» нормальному распределению с небольшой дисперсией: закон больших чисел (здесь – теорему Лапласа) никто не отменял. Тем не менее и f может дрейфовать, а для пипсовочных систем с очень небольшим м.о. сделки такой дрейф может оказаться критическим и сделать систему убыточной на полном интервале тестирования. У нас есть средства, достаточные для статистической оценки шансов такого дрейфа, – если есть свидетельства, подтверждающие, что схема Бернулли в данном случае работает.

К сожалению, эксперт Lucky_, даже урезанный в возможностях до единственной сделки в каждый момент времени, дает слишком много статистики. Для серьезного разработчика стратегии это скорее исключение, чем правило, так как чаще приходится делать очень коварные выводы на основании результатов тестирования, содержащих несколько сотен или даже десятков сделок (об этом - ниже). Увеличение объема статистики вполне закономерно приводит к соответствующему уменьшению относительной ширины кривой Гаусса и значительно снижает шансы на большие отклонения от ее центрального значения.

Для примера рассмотрим Lucky_ с далеко не самыми выгодными для него параметрами – 4, 80, 20, на лоте 0.1. Вначале проведем его тестирование на полном интервале времени («интервал А») – с 1 января 2004 по 4 апреля 2008 г. на ТФ Н1 на EURUSD. График баланса из отчета приложен ниже:

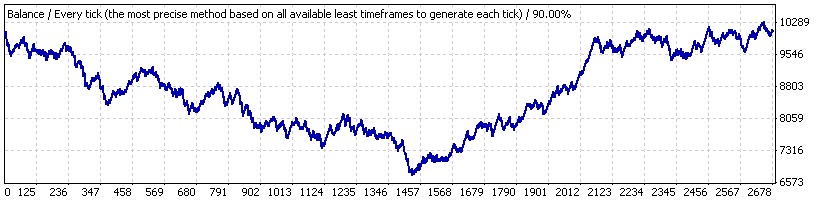
Как видим, результаты явно не впечатляющие. После проверки последовательности сделок с помощью нашего скрипта (на 1000 модельных сериях Бернулли) выясняется, что полную серию сделок можно считать соответствующей схеме Бернулли – как по прибыльным кластерам, так и по убыточным.

Отметим для себя параметры средних сделок:

Average profit trade

21.71

loss trade

-83.32

А теперь предположим, что мы на самом деле тестировали советник только на небольшом участке с 2005.10.21 по 2007.06.07 («интервал Б»), на котором стратегия показывает устойчивый рост. График - ниже:

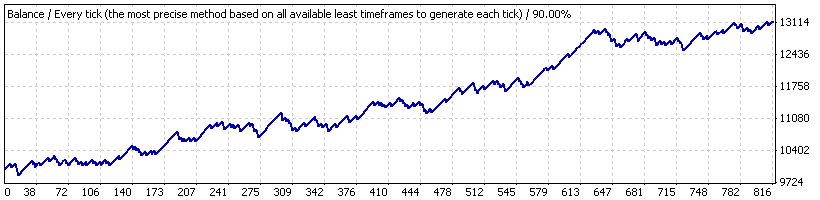
Результаты средних сделок:

Average profit trade

21.69

loss trade

-82.94

Средние сделки изменились незначительно, и поэтому можно считать, что они примерно постоянны вне зависимости от прибыльности стратегии на том или ином участке тестирования. В принципе это можно было понять и раньше – с учетом того, что сделки закрываются только по достижению определенной прибыльности/убыточности, заданной жесткими внешними параметрами.

Вторая экспресс-проверка на бернуллиевость (1000 модельных серий) снова подтверждает соответствие схеме Бернулли. Теперь запускаем скрипт с большим количеством серий Бернулли (65000) на результатах укороченного отрезка тестирования Б, а затем переносим результаты отдельных модельных серий Бернулли в MS Excel, чтобы построить гистограмму распределения доли прибыльных сделок:

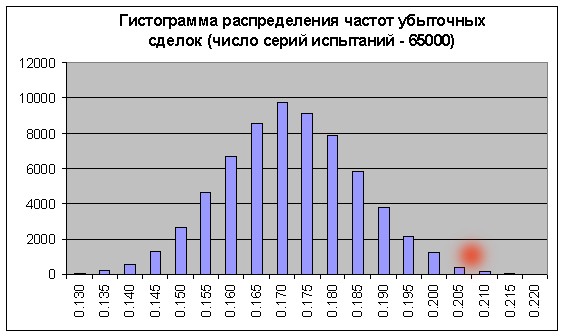
Очевидно, что частоты прибылей и убытков для достижения бесприбыльности должны соотноситься обратно пропорционально отношению их средних значений: r = 21.69/82.94 = 0.2615. Следовательно, частота убыточных сделок должна быть равна f = r/(1+r) = 0.2073. Видно, что это значение (см. красное пятно) находится далеко в области правого хвоста, причем сумма столбиков правее примерно соответствует 0.3% от суммы всех столбиков гистограммы, т.е. шансы бесприбыльности/убыточности – порядка 0.003. Примерно такая же величина получается при прямом применении теоремы Лапласа.

Что-то не так в датском королевстве: из отчета на интервале А мы хорошо знаем, что в первой его половине, перед этим участком роста, баланс пости столь же резво падал, причем участок падения по количеству сделок не меньше исследуемого Б. Если оценивать вероятность примерно такого участка падения баланса (уверенной убыточности) исходя из наших данных тестирования интервала Б, она станет вообще исчезающей (так как граничная частота f сдвинется еще больше вправо), а это как будто бы противоречит экспериментальным данным.

Проблема, вероятно, в том, что столь длинная серия сделок с прибыльностью, соответствующей участку Б, сама по себе является большим отклонением: тестирование на участке с января 1999 по начало мая 2008 выявляет, что стратегия фактически не является ни прибыльной, ни убыточной:

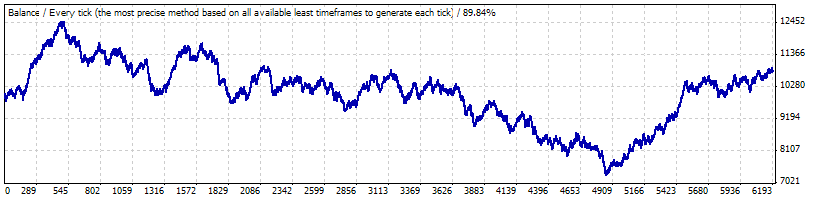
Матожидание сделки равно всего 0.17, а «естественная» частота убыточных сделок примерно равна ранее вычисленной f (0.2073) и составляет 0.2054.

Понятно, что оценки вероятностей, основанные на статистике редких событий (частота убыточных сделок на участке Б равна 0.1706 и отличается от «естественной» примерно на 2.8 «сигмы» в выгодную сторону), не могут быть достаточно надежными. Но «истинную» частоту мы не можем знать наверняка. Можно ли все же извлечь пользу из понятия «дрейф неудачи»?

4. «Дрейф неудачи»: оценка вероятности кратковременных «шоковых» просадок. Подход к снаряду № 2

По-видимому, можно, если ставить разумные, а не экстремистские цели, соответствующие «хвостам» распределений. Поставим задачу так: допустим, у нас имеются результаты тестирования на интервале Б. Мы уверены в том, что это схема Бернулли, и что м.о. прибыльной и убыточной сделок практически не зависят от того, что творится с балансом торгового счета. Попытаемся, исходя из крайне оптимистичных (фактически ошибочных!) оценок вероятности неудачи, прикинуть, насколько велики наши шансы на кратковременные, но глубокие, шоковые просадки. Именно такие дродауны оказывают самое разрушительное воздействие на психику трейдера, так как трейдер после этого внезапно начинает произносить мистические фразы типа того, что «рынок изменился» и даже «стал нерыночным».

Сразу оговоримся, что теорема Лапласа нам тут не слишком поможет, так как величина n*p*q, фигурирующая в ее формулировке, будет небольшой, порядка 10 и меньше (это примерно соответствует нескольким десяткам сделок). Основная идея в основе этого расчета заключается в том, что в очень коротких сериях сделок частота неудач может весьма существенно отличаться от «истинной», т.е. вероятности, т.к. распределение частоты неудачи – «сильно размазанное» из-за небольшого числа испытаний.

Отметим, что оценка кратковременной просадки – задача, существенно отличная от проблемы оценки максимальной длины убыточного кластера, т.к. просадка не обязательно состоит из одних только убыточных сделок. Воспользуемся нашим скриптом, генерируем 65000 серий длины 40 при «очень благоприятной» частоте неудачи 0.1706 («интервал Б») и построим такую же гистограмму, которую мы строили в Подходе к снаряду № 1:

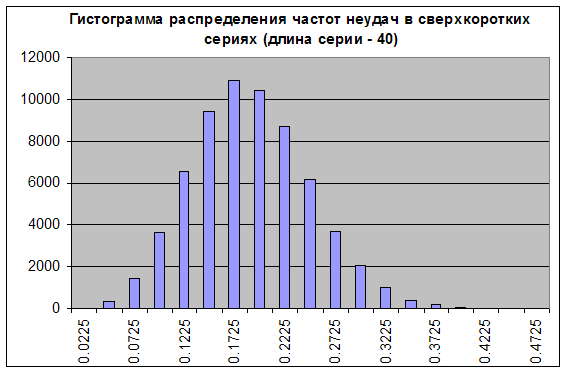
Как видим, ситуация кардинально изменилась: из острого распределение превратилось в пологое, т.е. его «относительная ширина» увеличилась. Вероятность того, что в серии длиной 40 мы получим нечто в диапазоне от практически бесприбыльной торговли (при частоте убыточных сделок 0.1975 средняя сделка составляет 0.25 пункта) до резко убыточной (при частоте неудач 0.3000 оценка м.о. сделки в этой серии равна 0.7*20-0.3*80=-10 пунктам), равна сумме столбцов с "0.2225" и правее, что составляет примерно 34% от общей суммы высот столбцов (65000). И это – оптимистичная оценка, так как пик распределения приходится на «оптимистичную» частоту 0.1706!

Вспоминая о гипотезе эргодичности, перекидывающей мостик от вероятностного распределения к пространству торговли, т.е. времени, получаем, что примерно как минимум 34% времени торговли система не будет приносить прибыль, а будет в среднем нести убытки. Эта цифра неплохо согласуется с данными из [4], согласно которым бернуллиева система примерно от 35 до 55% всего времени торговли находится в просадке.

Следует обратить внимание на то, что фактическая вероятность наткнуться на шоковую просадку не слишком сильно зависит от исходной «благоприятной частоты», как бы хорошо она ни выглядела. Это – особенность системы, связанная с ее бернуллиевостью, и это явление может быть смягчено только улучшением соотношения результатов средней прибыльной и убыточной сделок.

Кстати, именно эти оценки, основанные на генерации сверхкоротких серий, позволяют нередко очень надежно отмести результаты тестирования даже весьма «прибыльных» систем с десятками сделок на участке тестирования: несмотря на приличное положительное «матожидание» сделки, в случае бернуллиевости системы при таком небольшом количестве сделок шоковые просадки неизбежны.

Выводы

Несмотря на то, что нам так нравится разрабатывать логические конструкции, называемые гордым словом «МТС», мы иногда даже и не подозреваем, насколько много в них случайности – в том числе и такой, которую мы вообще не встречаем по результатам тестирования («черные лебеди»).

Так как результаты последовательных сделок, выраженные в двоичной системе счисления ("успех" или "неудача"), совсем нередко подчиняются схеме Бернулли, то они не имеют никакого явного отличия от схемы подбрасывания бутерброда с маслом. Это, конечно, не означает, что прибыльных систем не может быть: стратегия может быть и прибыльной, и робастной, даже если она идеально подчиняется схеме Бернулли. Это очевидно вытекает из того, что если и вероятность появления прибыльной сделки, и ее м.о. устойчиво выше тех же значений для убыточной, то стратегия явно прибыльна.

Читатель, не всегда общающийся с математикой "на Вы", должен неплохо понимать пользу моделей - даже если они совершенно не являются детерминистскими. Главная ценность моделей, адекватных реальному статистическому явлению, заключается в том, что они позволяют получить ценное знание о генеральной совокупности - информацию, которую невозможно получить непосредственно из скудных экспериментальных данных. В данном случае ценность схемы Бернулли существенно повышается благодаря исключительной простоте ее генерации и отсутствии "толстохвостостей" в ключевых распределениях вероятностей.

Завершим эту статью очень жестким вопросом: может быть, аналитическая часть подавляющего большинства ТС бесполезна, а основные усилия следует сосредоточить на эффективных и обоснованных методах управления капиталом ("Аналитика - ничто, управление капиталом - всё остальное!")?

Литература

1. Феллер В. Введение в теорию вероятностей и ее приложения, Том 1 – «Мир», 1964.

2. Taleb N. N. The Black Swan: Why Don’t We Learn that We Don’t Learn? - HIGHLAND FORUM 23, Las Vegas, November 2003. FIRST DRAFT, January 2004.

3. Талеб Н. Одураченные случайностью. Скрытая роль шанса на рынках и в жизни - М.: Интернет-трейдинг, 2002.
4. Винс Р. Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров, - John Wiley&Sons.
5. Р. Пардо. Разработка, тестирование, оптимизация торговых систем для биржевого трейдера, - John Wiley&Sons.
6. Ширяев А.Н. Основы стохастической финансовой математики, Том 1: Факты, модели - "Фазис", М., 1998.

7. Булашев С. В. Статистика для трейдеров. - М.: Компания Спутник +, 2003.