Теория категорий в MQL5 (Часть 10): Моноидные группы

Введение

В предыдущей статье мы продолжили рассматривать моноиды, взяв за основу действия моноидов как средство преобразования множеств моноидов путем расширения их возможных элементов. До сих пор в целом мы рассмотрели понятия: домены, морфизмы, аксиомы категорий вплоть до мономорфных расслоенных произведений и эпиморфных кодекартовых квадратов. Хотя некоторые могут возразить, что реализация концепций теории категорий требует более широкого изучения всех/большинства ее концепций, подход, принятый здесь, заключается в изучении того, какие идеи могут быть полезны с точки зрения базового или ограниченного взгляда на предмет. Каждая из этих статей (хотя в некоторых случаях концепции были заимствованы из предыдущих статей) продемонстрировала способность упрощать жизнь трейдеров, а в некоторых случаях улучшать торговые системы. В этой статье мы рассмотрим моноиды в группах. Как и действия моноидов, рассмотренные в предыдущей статье, они будут рассматриваться как переопределение моноида в момент принятия решения о сделке. Напомним, что действия моноидов рассматривались как расширение множества моноидов. Здесь мы будем переоценивать другой параметр моноида, а именно элемент равнозначности, поскольку мы еще раз переопределяем наши моноиды. В рамки этой статьи не входит построение полных торговых систем, как это было в некоторых предыдущих статьях, где мы создавали экземпляры класса сигналов и/или трейлинга советника с целью сборки полных советников со встроенным мастером MQL5. Вместо этого мы рассмотрим отдельные функции, являющиеся частью наших закодированных классов, действий и групп моноидов, и изучим, как они могут быть полезны трейдеру в ключевые моменты принятия решений.

Понимание групп моноидов

Как мы помним, моноиды - это множества, элементы равнозначности, принадлежащие этим множествам, и бинарные операции, которые используют любые два элемента множества и всегда возвращают элемент, который является членом множества. Кроме того, если какие-либо члены множества связаны с элементом равнозначности в бинарной операции, то результатом всегда будет этот элемент. Действия моноидов, которые были рассмотрены в нашей последней статье, представляют собой форму функции, определяемую множеством и бинарной операцией, которая связывает элементы множества моноидов с множеством этой функции и всегда выводит элемент, который является членом множества функции. Мы рассматривали их как средство преобразования моноида, потому что вывод бинарной операции моноида был закрытым, поскольку все результаты были строго членами множества моноидов.

Однако для начала было бы разумно указать, что между группами и моноидными группами нет различий. Единственная разница, заключается в том, что мы строго ссылаемся на множества (или домены), принадлежащие категории. Таким образом, моноидная группа, исходя из определения группы, является моноидом с дополнительным свойством, состоящим в том, что каждый элемент в наборе моноидов должен иметь обратный элемент. Когда элемент и его инверсия объединяются в пару в бинарной операции моноида, выход всегда является элементом равнозначности моноида.

Формально обратное свойство, которое отличает группу моноидов

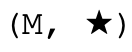
от обычных моноидов для каждого

имеется также обратный элемент

такой, что:

где e — элемент равнозначности моноида.

Применение для трейдеров будет рассмотрено так же, как и в предыдущей статье. Как вы помните, мы рассматриваем моноиды (множества) как набор вариантов решений, из которых может выбирать трейдер. В предыдущей статье мы рассматривали возможность увеличения размера этого набора с помощью действий моноидов. Мы изучили, какое влияние это окажет на производительность торговой системы, если мы расширим область действия конкретных моноидов на основе списка факторов, взвешивающих относительную важность точек принятия решений (параметров) торговой системы. Результаты оказались хуже среднего по сравнению с тем, что мы получили в статье, рассматривавшей ограниченные (по умолчанию) моноиды. В случае с группами моноидов мы, вместо того чтобы расширять объем наших множеств моноидов, вернемся к ограниченным моноидам, у которых было действие и которые были преобразованы в группы. Мы рассмотрим изменение состава множества после действия этого моноида, но реальная реализация торговой системы не будет рассматриваться в этой статье. Я предлагаю вам рассмотреть эту тему самостоятельно.

Реализация групп моноидов на MQL5

При настройке нашей среды MQL5 для реализации групп моноидов мы запустим IDE и создадим новый файл скрипта с помощью мастера.

Назовем наш скрипт ct_10 на соседней вкладке и нажмем Finish. Скрипт будет ссылаться на файл класса ct_10.mqh, который является модификацией класса ct_9.mqh, о котором мы говорили в предыдущей статье. Для полноты картины может быть полезно пройти этапы создания класса моноида, который был частью ct_9.mqh, о котором мы упоминали в двух предыдущих статьях. Как мы помним, наша базовая строительная единица — это класс элементов, который в основном представляет собой массив объектов типа данных T. Тип данных T устанавливается при инициализации элемента.

//+------------------------------------------------------------------+
//| ELEMENT CLASS                                                    |
//+------------------------------------------------------------------+
template <typename T>
class CElement                      : public CObject
   {
      protected:
      
      int                           cardinal;
      T                             element[];
      
      public:
      
      bool                          Cardinality(int Value) { ... }
      int                           Cardinality() { return(cardinal); }
      
      ...
                                    
                                    CElement(void)
                                    {
                                       Cardinality(0);
                                    };
                                    ~CElement(void) {};
   };

Класс элемента, в свою очередь, вызывается множеством (классом домена) как массив.

//+------------------------------------------------------------------+
//| DOMAIN CLASS                                                     |
//+------------------------------------------------------------------+
template <typename T>
class CDomain                       : public CObject
   {
      protected:
      
      int                           cardinal;
      CElement<T>                   elements[];
      
      public:
      
      bool                          Cardinality(int Value) { ... }
      int                           Cardinality() { return(cardinal); }
      
      ...
      
                                    CDomain(void)
                                    {
                                       Cardinality(0);
                                    };
                                    ~CDomain(void) {};
   };

Мы пошли дальше и определили не только класс категорий, формально определяющий моноидные группы как отличные от групп, но и классы морфизмов, гомоморфизмов и ряда других понятий. Поскольку они, как и класс категории, сами по себе не являются критическими для построения моноидного класса, мы не будем перечислять или рассматривать их в этой статье. Мы знаем, что моноид — это множество, элемент равнозначности и бинарная операция. Если бы нам нужно было дать определение бинарной операции, мы могли бы это сделать, перечислив наши параметры в форме перечисления. В последних двух статьях мы использовали что-то похожее на это.

//+------------------------------------------------------------------+
//| Enumeration for Monoid Operations                                |
//+------------------------------------------------------------------+
enum EOperations
  {
      OP_FURTHEST=5,
      OP_CLOSEST=4,
      OP_MOST=3,
      OP_LEAST=2,
      OP_MULTIPLY=1,
      OP_ADD=0
  };

Мы не будем пересматривать код для нашей статьи. Достаточно сказать, что он устанавливает средства, с помощью которых можно настраивать и определять бинарные операции для соответствующих элементов множества моноидов. Возможности здесь открываются интересные. Переходя к классу моноидов, создадим наш класс как публично наследуемый от класса домена вместо того, чтобы определять новый класс с экземпляром множества (домена). Это эффективный код, интуитивно показывающий, что моноид — это просто домен с бинарной операцией и прикрепленным к нему элементом равнозначности.

//+------------------------------------------------------------------+
//| Monoid Class                                                     |
//+------------------------------------------------------------------+
template <typename T>
class CMonoid                       : public CDomain<T>
   {
      protected:
      //double                        weights[];
      
      int                           identity;
      EOperations                   operation;
      
      public:
      
      double                        weights[];
      
      ...
      
      void                          Operation(EOperations Value) {  operation=Value; }
      EOperations                   Operation() { return(operation); }
      
      ...
      
                                    CMonoid(){ identity=0; operation=OP_ADD; };
                                    ~CMonoid(){};
   };

К этому классу мы затем добавляем две дополнительные аксиомы бинарной операции и элемент равнозначности. Наш элемент равнозначности, однако, не является другим экземпляром элемента. Он уже находится в массиве элементов домена. Вместо этого мы просто ссылаемся на индекс этого массива, указывающий на наш элемент равнозначности. Класс моноида может быть инициализирован автоматическим указателем в нашем скрипте, как показано в примере ниже.

Класс моноидных действий, описанных в предыдущей статье, унаследован от этого моноидного класса.

Однако для моноидных групп семантически нет разницы в коде класса между моноидом и моноидной группой. Мы можем лишь проверить требование инверсии с моноидными группами. Поэтому для наших целей класс группы моноидов будет иметь функцию проверки HasInversion, как показано ниже.

//+------------------------------------------------------------------+
//| Monoid Group Class                                               |
//+------------------------------------------------------------------+
template <typename T>
class CMonoidGroup                 : public CMonoid<T>
   {
      protected:
      
      public:
      
      bool                          HasInversion() 
                                    {  
                                       bool _has_inversion=true;
                                       
                                       for(int i=0;i<this.Cardinality();i++)
                                       {
                                          bool _has_inverse=false;
                                          
                                          for(int ii=0;ii<this.Cardinality();ii++)
                                          {
                                             if(Operate(i,ii)==Identity()){ _has_inverse=true; }
                                          }
                                          
                                          if(!_has_inverse){ _has_inversion=false; break; }
                                       }
                                       
                                       return(_has_inversion); 
                                    }
      
                                    CMonoidGroup(){};
                                    ~CMonoidGroup(){};
   };

В двух предыдущих статьях элементы класса моноида и действия моноида не составляли нормализованных данных. Это означает, что перед использованием в двоичных операциях их нужно было преобразовать в формат, допускающий справедливое сравнение. Этот формат в статье будет называться весами (weights). В предыдущих статьях эти значения весов рассчитывались и использовались во время выполнения. Здесь мы собираемся ввести в класс группы моноидов (monoid-group) параметры для установки, хранения и получения значений этих весов внутри класса. Все веса будут данными типа double.

      CMonoidGroup<int> _vg;        //valid inversion group
      CMonoidGroup<int> _ig;        //invalid inversion group
      
      _vg.Weights(5);             //set group size
      _ig.Weights(5);             //set group size
      for(int i=0;i<5;i++)
      { 
         CElement<int> _ve;_ve.Cardinality(1); _ve.Set(0,i-2);
         _vg.Set(i,_ve,true);      //set element
         _vg.SetWeight(i,double(i-2));  //set weight
         
         CElement<int> _ie;_ie.Cardinality(1); _ie.Set(0,i);
         _ig.Set(i,_ie,true);      //set element
         _ig.SetWeight(i,double(i));   //set weight
      }
      
      _vg.Operation(OP_ADD);      //set monoid operation to add
      _vg.Identity(2);            //set identity element index to 2
      
      _ig.Operation(OP_ADD);      //set monoid operation to add
      _ig.Identity(2);            //set identity element index to 2 as above or any index
      
      printf(" it is: "+string(_vg.HasInversion())+", vg has inversion, given the weights. ");
      ArrayPrint(_vg.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT);
      
      printf(" it is: "+string(_ig.HasInversion())+", ig has inversion, given the weights. ");
      ArrayPrint(_ig.weights,0,",",0,WHOLE_ARRAY,ARRAYPRINT_LIMIT);

Чтобы увидеть этот код в действии, создадим экземпляр группы моноидов и запустим проверку с помощью наших функций класса, чтобы увидеть, что мы получим на выходе. Наш код, который прилагается к этой статье, просто подтверждает инверсию в множестве. Каждый элемент должен иметь инверсию по отношению к элементу равнозначности.

2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: true, vg has inversion, given the weights. 
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)-2, -1,0,1,2
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1)it is: false, ig has inversion, given the weights. 
2023.06.16 17:17:41.817 ct_10 (USDJPY.i,M1) 0,1,2,3,4

Для практических целей группе моноидов '_vg' был присвоен размер 5, но ее фактический размер не ограничен, поскольку для соответствия всем аксиомам группы любое сопряжение чисел в двоичной операции всегда должно приводить к числу, которое является членом множества группы. С тем, что мы использовали, сопряжение двух и одного приведет к трем. Этого значения нет в множестве. Таким образом, _vg — это несвязанный набор целых чисел (Z).

Использование групп моноидов в алгоритмической торговле

В предыдущих двух статьях, с тех пор как мы начали рассматривать моноиды, мы использовали их в качестве точек принятия решений. В частности, они использовались при принятии решений, касающихся:

- продолжительности периода ретроспективного анализа для рассмотрения;

- используемого таймфрейма;

- применяемой цены;

- используемого индикатора;

- торгового метода (следование за трендом или торговля против тренда).

Являясь точками принятия решений, множества каждого из этих моноидов представляли собой варианты, с которыми мог столкнуться трейдер. Что не было четко упомянуто в этих статьях, хотя и было реализовано, так это взвешивание каждого элемента в соответствующих множествах моноидов. Перед выполнением моноидных бинарных операций по всем элементам множества для выбора элементы необходимо было нормализовать. В некоторых случаях, как, например, с применяемой ценой, было непросто сравнивать ценовые бары, чего требуют некоторые торговые ситуации. Поэтому нам нужно было найти способ количественной оценки этих элементов множества таким образом, чтобы он адаптировался по мере изменения ценового действия (или любой другой выбранной базовой метрики) со временем. Итак, эта "количественная оценка" элементов множества и есть то, что мы будем называть весами в этой статье.

После взвешивания значений наших элементов, чтобы использовать группы, нам нужно будет применить функцию OperateModulo в измененном классе действий моноида. Фактическое множество групп, которое находится в нашем классе действий, не указано, поскольку это просто список целых чисел до размера, определяемого нашими входными данными для скрипта. То, что регистрируется, является относительным множеством для этой группы, поскольку действие по модулю на начальном множестве обязательно приводит к повторениям.

Ниже показана реализация функции Operate в виде метода с классом действий моноидов.

      int                           OperateModulo(int Index,int Modulo=1)
                                    {
                                       int _operate=-1;
                                       
                                       if(Index>=0 && Index<this.Cardinality())
                                       {
                                          int _value=int(round(set.weights[Index]));
                                          
                                          _operate=_value%Modulo;
                                       }
                                       
                                       return(_operate);
                                    }

Таким образом, как только наши множества моноидов преобразуются в меньшее "круговое" множество, бинарная операция для этого меньшего моноида при объединении любых двух элементов может вывести тот, который находится дальше всего от элемента равнозначности, который в нашем случае всегда будет средним индексом. Установка размера группы моноидов требует, чтобы размер был нечетным числом.

Если два элемента равноудалены от равнозначности, то выбирается элемент равнозначности. Итак, подытоживая наше моноидное действие здесь, мы эффективно нормализуем базовое моноидное множество в группу. Затем мы примем решение о соединении элементов на основе их значения в множестве действий моноида с бинарной операцией действия моноида.

Так как мы не кодируем и не тестируем советник для этой статьи, для иллюстрации результатов групп моноидов, на каждом из наших пяти вышеупомянутых параметров мы будем печатать набор моноидов с вариантами, с которыми сталкивается трейдер, веса, к которым эти установленные значения преобразуются, значения действия моноида для этих весов, которые дают значения группы моноидов, и относительное множество этой группы моноидов. Обратите внимание, что мы снова ссылаемся на относительные множества, начиная с предыдущей статьи, потому что для того, чтобы иметь множество моноидных действий в виде группы, мы будем использовать модуль от размера ввода, чтобы нормализовать и подогнать все значения наших весов ко множеству действий, которое также будет группой. При нормализации этих значений по модулю мы неизбежно столкнемся с повторами, поэтому набор действий в строгом смысле не является группой, а является относительным множеством группы, члены которой просто составляют все целые числа, начиная с нуля до размера ввода минус один.

Наши логи завершатся элементами множества действий, которое относится к группе, как указано выше. Затем читатель должен перенести вычисленные значения в каждом моноиде действий из моноида таймфрейма в моноид решения, сделав выбор в соответствии с аксиомами групп, описанными выше. В групповом множестве, как и в случае с моноидами, если какой-либо из парных элементов является равнозначным, то на выходе имеем неравнозначный элемент. Кроме того, если парные элементы обратны друг другу, то на выходе имеем элемент равнозначности.

Кроме того, может быть полезно сделать выбор, начиная с временных рамок, а затем использовать период ретроспективного анализа, в отличие от того, что мы рассматривали в предыдущих двух статьях. Вот как мы получим наши веса для моноида таймфрейма с учетом сказанного.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void WeighTimeframes(CMonoidGroup<ENUM_TIMEFRAMES> &G)
   {
      for(int i=0;i<G.Cardinality();i++)
      {
         ResetLastError();
         int _value=0;
         ArrayResize(__r,3);//ArrayInitialize(_buffer,0.0);//ArraySetAsSeries(_buffer,true);
         if(CopyRates(_Symbol,__TIMEFRAMES[i],0,3,__r)>=3)
         {
            _value=int(round(10000.0*fabs(__r[0].close-__r[1].close)/fmax(_Point,fabs(__r[0].close-__r[1].close)+fabs(__r[1].close-__r[2].close))));
         }
         else{ printf(__FUNCSIG__+" Failed to copy: "+EnumToString(__TIMEFRAMES[i])+" close prices. err: "+IntegerToString(GetLastError())); }
         
         ResetLastError();
         if(!G.SetWeight(i,_value))
         {
            printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError()));
         }
      }
   }

Обратите внимание, что все взвешивания теперь будут нормализованы к целочисленному формату, потому что мы хотим использовать модуль при их преобразовании с помощью действия моноида в множество относительно группы. Таким образом, поскольку взвешивание было положительным значением типа double, которое никогда не было больше единицы, для наших таймфреймов мы преобразуем его в целое число, которое может быть любым значением от 0 до 10 000. Кроме того, наш входной параметр размера для таймфреймов, по умолчанию равный 51, будет значением, которое мы используем для получения остатка, члена множества группы. Остальные значения хранятся в массиве весов класса моноидного действия.

Итак, если мы прикрепим наш скрипт к графику USDJPY на минутном таймфрейме, то увидим следующий результат для моноида таймфрейма по состоянию на 15.06.2023.

2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)with an input size of: 21 timeframe weights, and their respective monoid action values (group normalised) are: 
2023.06.16 17:17:41.818 ct_10 (USDJPY.i,M1)7098, 8811, 1686, 1782, 1280, 5920, 1030, 5130
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1) {(0),(12),(6),(18),(20),(19),(1),(6)}
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1) 
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)and action group values (relative set) are: 
2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20

Мы используем немного измененный набор таймфреймов из наших прошлых статей. Опять же, вам решать, какой набор таймфреймов лучше всего подходит для предмета вашего изучения. Если мы отобразим логи моноида ретроспективного анализа, то увидим следующее.

2023.06.16 17:17:41.819 ct_10 (USDJPY.i,M1)with an input size of: 5 lookback weights, and their respective monoid action values (group normalised) are: 
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)3149, 1116, 3575, 3779, 7164, 8442, 4228, 5756
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(4),(1),(0),(4),(4),(2),(3),(1)}
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are: 
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 0,1,2,3,4

Мы видим, что на моноидном таймфрейме был выбран часовой таймфрейм. Повтор фактического окончательного выбора в каждом моноиде, следуя групповым аксиомам, не реализован в этой статье или прилагаемом коде. Вы можете сами исследовать и сделать этот первый шаг в моноидных группах, в направлении, которое, на ваш взгляд, лучше всего подходит для вашей стратегии. Ниже приведены логи использованной цены при периоде ретроспективного анализа, равном 8.

2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)with an input size of: 21 appliedprice weights, and their respective monoid action values (group normalised) are: 
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)1469254, 1586223, 1414566, 2087897
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) {(10),(9),(6),(14)}
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1) 
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)and action group values (relative set) are: 
2023.06.16 17:17:41.820 ct_10 (USDJPY.i,M1)0, 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12,13,14,15,16,17,18,19,20

Заключение

Мы рассмотрели, что такое группы моноидов, введя понятие симметрии в типичный моноид, а также добавили дополнительную аксиому, что все члены группы моноидов должны иметь инверсию, а бинарные операции между зеркальными элементами всегда должны выводить элемент равнозначности группы моноидов. Это было продолжение нашей предыдущей статьи, в которой мы рассматривали моноидные действия.

Как и в предыдущей статье, мы показали, как группы моноидов могут быть полезными для трейдеров в ограниченных множествах моноидов. В этой статье мы взяли множества моноидов как фиксированный набор вариантов выбора трейдера на данном этапе. В предыдущей же статье мы пытались изучить влияние расширения выбранных меножеств моноидов на эффективность торговли.

Здесь мы лишь "намекнули" на потенциал групп моноидов, не показав советников с их участием. Читателю предлагается развить эту тему дальше и реализовать возможность выбора в каждом моноиде, следуя правилам групп, которые мы упомянули, но не воплотили в код.

В следующей статье мы рассмотрим еще одну концепцию теории категорий.