Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Kolmogorov é um homem mais esperto do que a maioria daqueles que olham para o monitor. E suas exigências à previsão da BP são simples: expectativa = const e ACF periódica.
Agora, o que há a dizer é o seguinte.
Eu olho para as distribuições incrementais e como elas mudam seus momentos estatísticos dependendo dos intervalos de leitura das cotações, e percebo que os preços de mercado NÃO têm a propriedade da auto-similaridade. Esta propriedade é exclusiva para processos com distribuições estáveis, infinitamente divisíveis (por exemplo, normais) de incrementos - como o movimento Brownian. Este não é o caso no mercado.
Obviamente, Mandelbrot e seus companheiros, que não têm conhecimento de física (e pior ainda - eles têm conhecimento, mas o escondem cuidadosamente), enganaram intencionalmente as pessoas desesperadas, para que fossem escalar em dados de carrapatos e pequenos períodos de tempo, e enchessem seus bolsos inferiores perdendo seus depósitos.
Bem, lá vai você!
Pesquisa sobre
http://tpq.io/p/rough_volatility_with_python.html
mesmo https://hal.inria.fr/hal-01350915/documentAgora, o que há a dizer é o seguinte.
Eu olho para as distribuições incrementais e como elas mudam seus momentos estatísticos dependendo dos intervalos de leitura das cotações, e percebo que os preços de mercado NÃO têm a propriedade da auto-similaridade. Esta propriedade é exclusiva para processos com distribuições estáveis, infinitamente divisíveis (por exemplo, normais) de incrementos - como o movimento Brownian. Este não é o caso no mercado.
Obviamente, Mandelbrot e seus companheiros, que não têm conhecimento de física (e pior ainda - eles têm conhecimento, mas o escondem cuidadosamente), enganaram intencionalmente as pessoas desesperadas, para que fossem escalar em dados de carrapatos e pequenos períodos de tempo, e enchessem seus bolsos inferiores perdendo seus depósitos.
É isso aí!
Você já trouxe teorias conspiratórias para a mistura... outra carga de porcaria.
Leia o assunto:
http://inis.jinr.ru/sl/vol2/Physics/Динамические%20системы%20и%20Хаос/Федер%20Е.,%20Фракталы,%201991.pdf
Só para deixar claro o que eu pretendo.
Comecei agora a trabalhar no fluxo de 60 pedidos de Erlang (lendo as citações de carrapatos, em média, uma vez por minuto).
Temos o seguinte histograma para os incrementos do par EURJPY, por exemplo:
Estatísticas:
Esta é praticamente uma distribuição Laplace.
A soma dos incrementos (~preço) e dos módulos de incremento (~dispersão) tem distribuição normal a um volume de amostra bastante grande (um dia - para M1 ou uma semana - para M5) de tal SP.
Portanto, o objetivo é chegar a uma distribuição Laplace pura, então teremos realmente um análogo direto do processo Ornstein-Uhlenbeck com um retorno à média.
Eu também gostaria de adivinhar que seções da história ele usa para construir suas cartas, há seções de tendências para vários meses, e há seções laterais
Assim como o princípio de "pular" de M1 para M5 não é claro, ele precisa de consistência ou pelo menos de uma justificativa. Ele seria inestimável lá com tais talentos, eles também acrescentam com sucesso meses, depois trimestres, depois estações = a produção dos dados estatísticos corretos
)))
Só para deixar claro o que eu pretendo.
Acabo de começar a trabalhar no 60º fluxo de pedidos de Erlang (lendo as citações de carrapatos, em média, uma vez por minuto).
Temos o seguinte histograma para os incrementos do par EURJPY, por exemplo:
Estatísticas:
Esta é praticamente uma distribuição Laplace.
A soma dos incrementos (~preço) e dos módulos de incremento (~dispersão) tem distribuição normal a um volume de amostra bastante grande (um dia - para M1 ou uma semana - para M5) de tal SP.
Portanto, o objetivo é chegar a uma distribuição Laplace pura, então teremos realmente um análogo direto do processo Ornstein-Uhlenbeck com um retorno à média.
Em geral, vejo que a curtose é reduzida, as caudas são recolhidas ---> de Laplace para normal, de normal para uniforme. Então o que está no início? Não Laplace? Porque é facilmente descrito por um expoente, se você tomar um dos lados.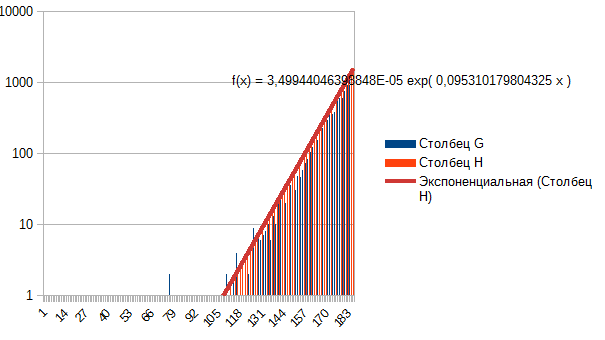
Esta é a janela de minutos-mês do EURUSD.