Locatário - página 6
Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Não, não. Não está errado. Aqui está a dependência do montante de retirada, que decorre da fórmula iterativa (em vermelho), e da dependência analítica (em azul).
Você pode ver que elas coincidem e há um máximo em k (na página anterior do tópico).
Claramente, você não tem retiradas discretas, mas necessariamente retiradas contínuas em partes iguais. Portanto, não há solução para se retirar de forma diferente em períodos diferentes. Portanto, não há solução para retirar tudo no final sem antes ter se retirado. Isto não decorre das condições do problema, mas das fórmulas que você aplica (k é fixo, não variável ki, i=0...T)
Total de fundos retirados
o efeito se torna tangível se a taxa de crescimento for suficientemente alta
Eu tenho dependências similares.
Agora estou tentando decompor a expressão para o derivado em poderes de k, mas isso não é bom - tenho que manter seis ordens de magnitude. É evidente que isto não pode ser resolvido de forma analítica. Talvez haja outras idéias? Alguém mencionou os difurcadores...
Eu tenho dependências similares.
Agora estou tentando decompor a expressão para o derivado em poderes de k, mas isso não é bom - tenho que manter seis ordens de magnitude. É evidente que isto não pode ser resolvido de forma analítica. Talvez haja outras idéias? Alguém mencionou os difurcadores...
É um pouco complicado do ponto de vista analítico. Em q e t. Depende, de alguma forma, de uma forma complicada :) Conforme q aumenta, conforme t aumenta, a fração de remoção ótima diminui consistentemente
Eu tenho dependências similares.
Agora estou tentando decompor a expressão para o derivado em poderes de k, mas isso não é bom - tenho que manter seis ordens de magnitude. É evidente que isto não pode ser resolvido de forma analítica. Talvez haja outras idéias? Alguém mencionou os difurcadores...
Você pode ir do particular para o geral. Por exemplo, se t = 1, você pode retirar o dinheiro apenas uma vez, e portanto você tem que retirá-lo no valor de q. Em seguida, considere o caso para t = 2, t = 3, etc.
Isto é, se em t = 2 é ideal retirar menos de q de cada vez, então encontre um extremo e generalize para todos q em t = 2.
Da mesma forma para t = 3, t = 4 etc.
Do valor do extremo, será possível obter o tamanho da retirada como f(t)
Um esquema de navio conectado pode ser considerado para compor o DU.
Volume inicial da primeira embarcação B0
Você pode ir do particular para o geral. Por exemplo, se t = 1, você pode retirar o dinheiro apenas uma vez, e portanto você tem que retirá-lo no valor de q. Em seguida, considere o caso para t = 2, t = 3, etc.
A partir do valor do extremo, conseguiremos obter o tamanho da retirada como f(t)
Talvez você esteja certo. Exceto que para t = 3 já temos de acordo com a equação
grau k - três na primeira derivada df(k)/dk=0, e precisamos procurar as raízes da equação cúbica com tudo o que ela implica... Ou seja, não podemos ir além de t=3 neste cenário. Recordar que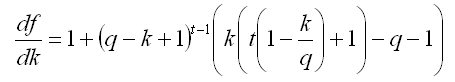 
, e para t=1 tamanho ideal k=q, para t=2 k=q, para t=3 k=q. Mas aumentar ainda mais o t e resolver analiticamente não funciona. Se você resolver numericamente, você pode ver que na taxa de crescimento do depósito q está dentro de 10% por mês, a taxa ideal de retirada se torna inferior a q em t>30 meses.
A conclusão é a seguinte: se a confiabilidade do TS for tal que a vida média do depósito não exceda 3 anos, então o comportamento ideal é um levantamento mensal de todos os lucros obtidos (o depósito não está crescendo). Caso contrário, precisamos encontrar uma solução analítica para a porcentagem ótima de retirada k e agir de acordo com a fórmula. Este cenário garante o máximo de dinheiro de bolso durante o tempo de vida esperado do depósito.
A fim de fazer DU podemos considerar o esquema de embarcações conectadas.volume inicial da primeira embarcação B0
Se as embarcações (fluxo de fluido) estiverem em equilíbrio dinâmico (ou seja, quanto fluido por unidade de tempo flui para a primeira embarcação tanto quanto flui da última) o problema sobre o nível de água em cada embarcação é elementar e não é reduzido ao problema do depósito. Se para considerar as embarcações em processo de enchimento, não está clara a analogia com o depósito. avtomat ,explique, por favor, o que você quis dizer com propor tal interpretação?
P.S. O apelo para obter uma solução analítica aproximada da equação df/dk=0 ainda é válido. Qualquer idéia é bem-vinda.