Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
OK. Aqui estão os dados.Parecemos ter nos entendido mal. Meus sentimentos sobre anormalidade não se aplicam ao gerador, mas ao mercado. Construa uma distribuição dos primeiros incrementos e veja por si mesmo.
Bem, para o cavalo esférico no vácuo, ou seja, para uma distribuição normal garantida - sim, é improvável. Bem, os verdadeiros não são cavalos em um vácuo. Há 5 ou 6 s.c.e. e até 10.
Tio, por favor, aqui está outra foto agora da libra de 1971, os diários. Pode haver um único disparo (e a propósito não há um :), o mais importante é que ele não se torne um padrão. Certo?
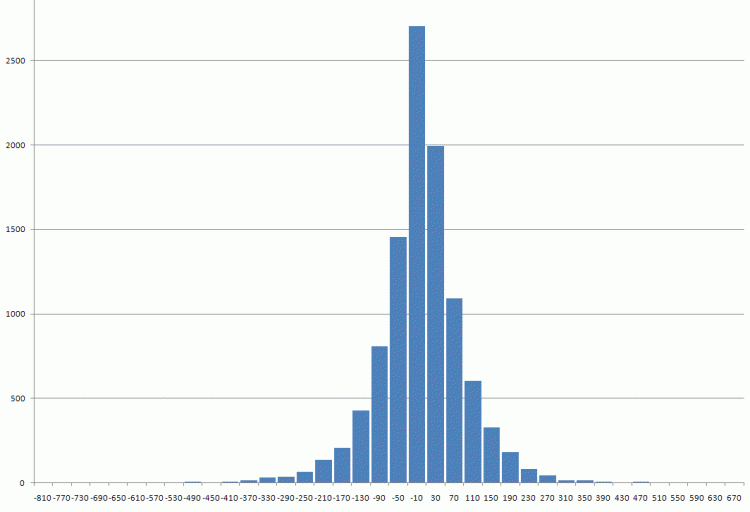
Os dados para verificação são anexados.Primeiras diferenças de libras desde 1971.
>>S. Talvez ele deva ser verificado quanto à estacionaridade :)
Tio, por favor, aqui está outra foto agora da libra de 1971, os diários. Pode haver um único disparo (e a propósito não há um :), o mais importante é que ele não se torne um padrão. Certo?
Os dados para a verificação estão anexados.As primeiras diferenças na libra desde 1971
Eu lhe chamaria uma distribuição Laplace a olho nu.
Eu a chamaria de distribuição Laplace a olho nu
A chave é que não há 5-6-10 sigmas. Caso contrário, sim, mas você tem que testá-lo. E, no entanto, pode ser que esteja tudo bem.Ilya, aqui está uma sugestão: aproximar esta distribuição por uma distribuição normal. E depois veja como os histogramas reais e a aproximação da curva gaussiana são diferentes um do outro. Não se limite a três sigmas, olhe para cima pelo menos dez.
Outra verificação trivial: calcular os primeiros momentos desta distribuição e compará-los com os momentos da distribuição normal.
O fenômeno das caudas gordurosas em séries financeiras é conhecido há muito tempo. O que você quer provar para mim?
Ilya, aqui está uma sugestão: aproximar esta distribuição por uma distribuição normal. E depois veja como os histogramas reais e a aproximação da curva gaussiana são diferentes um do outro. Não se limite a três sigmas, olhe para cima pelo menos dez.
Outra verificação trivial: calcular os primeiros momentos desta distribuição e compará-los com os momentos da distribuição normal.
O fenômeno das caudas gordurosas em séries financeiras é conhecido há muito tempo. O que você quer provar para mim?
A conversa foi sobre 5-6-10 RMS. Não vejo um padrão em sua aparência.
A chave é que não há 5-6-10 sigma. Como está, sim, mas precisa ser testado. E mesmo assim, pode ser normal.é altamente improvável. Distribuições normais são normalmente encontradas na natureza onde uma variável aleatória "grande" é a soma de um grande número de variáveis aleatórias "pequenas" distribuídas de uma certa forma (mas de forma idêntica). Um exemplo importante é o movimento browniano, ao qual tantas páginas já foram dedicadas no próximo tópico. No caso do mercado, a lei de formação de preços está longe disso, pois para obter uma normal, é necessário um número muito grande de "distúrbios" externos - que devem ser o fator principal na formação da distribuição. Mas não achamos que o preço no mercado é ruído, não é mesmo?
Em um gráfico, puramente visual, e você não verá que 5-6-10.
Em algum lugar eu tinha até mesmo um gráfico mostrando as diferenças. Se você pegar os dois primeiros momentos da distribuição e pensar neles como momentos de aproximação do normal, a diferença de freqüências por 3, 4, 5, etc. sigmas é fácil de calcular.
Não me lembro dos números exatos, mas a freqüência real de desvio de 3 sigma é 3-4 vezes maior do que a gaussiana (Gaussiana 0,3%, real mais de 1%). O desvio de 4 sigma ocorre na realidade mais frequentemente do que o gaussiano por cerca de 15 vezes. Para 5 sigma a diferença é dezenas de vezes, se não centenas. E assim por diante.
Desde que você não avalie os riscos, você não se importa se é gaussiano ou não.
P.S. A propósito, parece que, segundo Taleb, o LTCM entrou em colapso precisamente por causa da subestimação dos riscos. Um desvio de 10 sigmas foi considerado um evento raro insignificante. E foi exatamente isso que aconteceu.
Não me lembro dos números exatos, mas a freqüência real de desvio de 3 sigma é 3-4 vezes a gaussiana (gaussiana 0,3%, real mais de 1%). O desvio de 4 sigma ocorre na realidade com mais freqüência do que o gaussiano por cerca de 15 vezes. Para 5 sigmas a diferença é dezenas de vezes. E assim por diante.
...o que mais uma vez é uma prova a favor de Laplace.
Desde que você não avalie os riscos, você não se importa se é gaussiano ou não.
Você pode me dizer como abordar a avaliação de risco?