Território de probabilidade - página 8

[Yury Reshetov]

bowie:

O algoritmo para ganhar um jogo de atirar moedas é simples: se receber caudas, aposte em caudas; se receber cabeças, aposte em cabeças. Se o número de voltas for infinito, ganha).

Se a moeda estiver torta, a expectativa é positiva. Este é o algoritmo de C. Shannon. Se a moeda for perfeita, então atire-a ao ar até perder o ânimo, a expectativa será zero, porque não depende do número de tentativas.

[Ratibor Shokhirev]

Reshetov:
Если монетка кривая, тогда матожидание будет положительным. Это алгоритм К. Шеннона. Если монетка идеальная, то хоть до потери пульса подбрасывай, матожидание будет нулевым, т.к. оно не зависит от количества испытаний.

Shannon é sem dúvida fixe para conseguir tantos números num só lugar. ) É mais fácil com uma moeda. Caudas e cabeças formarão "listras de cabeças" e "listras de caudas" se houver atiramentos suficientes. Cada vez que aposta no lado anterior, o jogador espera entrar numa das listras de cauda. Expectativa igual a zero não é contestada. ) Um número infinito de lances permite ao jogador parar quando está num bom equilíbrio.

Se o jogo permitir aumentar/diminuir as apostas antes de cada lançamento, um jogador pode aumentar a aposta após cada vitória e diminui-la após cada perda. Parece-me que com tal abordagem o pagamento esperado seria ligeiramente acima de zero. Desde que o capital inicial seja suficiente).

[Yury Reshetov]

bowie:

Shannon é sem dúvida fixe para conseguir tantos números num só lugar. ) É mais fácil com uma moeda. Se forem feitos lançamentos suficientes, cabeças e caudas formarão "listras de cabeça" e "listras de cauda". Cada vez que aposta no lado anterior, o jogador espera entrar numa das listras de cauda. Expectativa igual a zero não é contestada. ) O número infinito de lances permite que o jogador pare quando está no plus suficiente para ele.

Se o jogo pressupõe a possibilidade de aumentar/diminuir as apostas antes de cada lançamento, um jogador pode aumentar a aposta após cada vitória e diminuí-la após cada perda. Parece-me que com esta abordagem o pagamento esperado será um pouco mais elevado do que zero. Desde que tenhamos capital inicial suficiente.

A probabilidade de o jogador, mais cedo ou mais tarde, obter o bordo a seu favor no caso de uma moeda perfeita é igual a 1, ou seja, é verdade de acordo com a lei dos arcinus. Se ele tem ou não capital suficiente é outra questão. A lei de arcinus diz apenas que o capital a uma aposta constante é inferior ao infinito, a fim de obter uma vantagem.

Uma tira, ou seja, uma série contínua de cabeças e caudas não contradiz quaisquer teorias, mas as vantagens também não dão. Se alguém tiver sorte, terá uma maré de sorte. Se tiver azar, terá má sorte. Não tem qualquer efeito na expectativa matemática, mas apenas na sorte, ou seja, a variância e a lei dos arcsinus.

[Vasiliy Sokolov]

Reshetov:

A probabilidade de um jogador obter mais cedo ou mais tarde uma vantagem no caso de uma moeda perfeita é 1, ou seja, é verdade de acordo com a lei dos arcinus. Se ele tem ou não capital suficiente é outra questão. A lei de arcinus apenas diz que, com uma aposta constante, é preciso menos do que o infinito para se conseguir uma vantagem.

E listras, ou seja, séries contínuas de cabeças e caudas não contradizem quaisquer teorias, mas também não dão uma vantagem. Quem tiver sorte, terá uma maré de sorte. Se tiver azar, terá má sorte. Não tem qualquer efeito na expectativa matemática, mas apenas na sorte, ou seja, a variância e a lei dos arcsinus.

Reshetov, deixa-te de tretas! O que tem a lei do arcinus a ver com isso? O início da ultrapassagem de desempenho não significa que será suficiente para passar para a zona de rendimento positivo e não durará o suficiente para manter esse rendimento na zona positiva.

[Vladimir Gomonov]

C-4:
Reshetov, deixa-te de tretas! O que tem a lei do arcinus a ver com isso? O início de uma ultrapassagem na zona de rendimento positivo não significa que será suficiente para passar para a zona de rendimento positivo, nem tempo suficiente para manter esse rendimento na zona positiva.

Estão ambos errados :)

Na realidade, todas as moedas estão tortas. Assim, a Shannon tem razão. Eu também tenho. ;)

[Ratibor Shokhirev]

Há um guião como este. E há dúvidas sobre MathRand(). Quem pode dizer o quê? )

//+------------------------------------------------------------------+
//|                                                         Coin.mq5 |
//|                                                     [e-mail] |
//|                                                     [e-mail] |
//+------------------------------------------------------------------+
#property copyright "[e-mail]"
#property link      "[e-mail]"
#property version   "1.00"
#property script_show_inputs
input int attempt=8;//количество подбрасываний
input bool z=0;//первая ставка 1 или 0 (орел/решка)
input bool as=true;//true== увеличивать лот при каждом выигрыше/ false== уменьшать

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   bool win=z;
   uint prev_count=0,tickcount=0;
   int coin=-1; 
   //int attempt=y;
   int a_rate=0;
   int b_rate=0;
   double lot=1;
   double dep=256-1;
   double div=0.0;
   bool d  = (as==true) ? div=1.009 : div=0.009;
   for(int x=0;x<attempt;x++) 
   {
    tickcount=GetTickCount();    
    while(prev_count==tickcount)
    {tickcount=GetTickCount();}
    
    MathSrand(tickcount);
    coin=MathRand()+x;
    coin=MathMod(coin,2);
    //Print(coin);
    if(coin==1 && win==1){a_rate=a_rate+1;dep=dep+lot; lot=lot*div;}
    if(coin==0 && win==0){a_rate=a_rate+1;dep=dep+lot; lot=lot*div;}
    if(coin==0 && win==1){b_rate=b_rate-1;dep=dep-lot;lot=1;}
    if(coin==1 && win==0){b_rate=b_rate-1;dep=dep-lot;lot=1;}
    if(coin==1){win=1;}
    if(coin==0){win=0;}
    prev_count=tickcount;
   }
   Print("Подбрасываний= "+attempt);
   Print("Угаданных= "+a_rate);
   Print("Неугаданных= "+b_rate);
   Print("Деп= "+dep);
  }
//+------------------------------------------------------------------+

[Boris Odintsov]

07041982:

Proponho discutir aqui os métodos e técnicas de utilização da teoria da probabilidade para construir sistemas de comércio. Apresentarei os meus pensamentos sobre este assunto sob a forma de teses:

1) A probabilidade de continuação da tendência em qualquer parte em qualquer momento é maior do que a probabilidade da sua inversão. Daí, a regra de ouro do comerciante: negociar apenas com a tendência.

2) A probabilidade de ganhar com uma entrada aleatória e o mesmo TP e SL tende a 50% com SL e TP crescentes.

3) A probabilidade de ganhar quando se negoceia com um lote dinâmico é menor do que quando se negoceia com um lote fixo. Cheguei a esta conclusão por mim próprio. Tentarei prová-lo: digamos que temos TS, que desencadeou alternadamente TP e SL, ou seja, SL-TP-SL-TP-SL-TP, enquanto SL = TP. A propagação não é tida em conta para facilitar a compreensão. Quando negociamos com um lote fixo, obtemos, por exemplo: -$10+$10-10$+$10-10$+$10$+$10$=0. Quando negociamos com lote dinâmico obteremos -10%+10%-10%+10%-10%+10%+10%+10% e não nos levará a lucro zero, mas será uma perda. Por exemplo, o depósito era 100, obtivemos: 100-10%=90; 90+10%=99; 99-10%=89,1; 89,1+10%=98,01; 98,01-10%=88,209; 88,209+10%=97,0299, o que era necessário para provar, a perda é visível.

Aguardo os vossos comentários e críticas construtivas se alguém não concordar com a minha terceira tese. Se alguém tiver quaisquer outras ideias sobre o uso da teoria da probabilidade, por favor fale mais alto.

Vou generalizar um pouco.

Suponha que sl (perda) e tp(lucro) são fixados em pontos de moeda.

Suponhamos que temos uma série suficientemente grande de N ofícios.

N=N1+N2, onde N1 - número de negócios executados em tp, N2 - número de negócios executados em sl.

Obviamente, o seu sistema de negociação será rentável se:

N1*tp - N2*sl >= spread * N

Continue, faça as contas - divida as partes esquerda e direita por N.

tp*N1/N - sl*N2/N >= spread

N1/N com o número de transacções tendentes ao infinito não é mais do que a probabilidade de um negócio lucrativo, chamemos-lhe p=N1/N

N2/N - então a probabilidade de um comércio perdido, e será igual a 1-p

Temos:

p*tp - (1-p)*sl >=spread

Ou de outra forma:

p>=(sl + spread)/(sl+tp)

É para isto que criamos sistemas de comércio. A probabilidade de querermos aumentar. Mas deve sempre lembrar-se do que deve ser mais do que ter lucro.

Por exemplo, se ignorar o spread, e com igual tp e sl, o seu sistema de negociação será rentável se p>0,5 ... etc.

Se fizer alterações como o lote dinâmico, as coisas tornam-se muito mais complicadas, e a probabilidade de um comércio lucrativo deve ser maior do que no caso acima mencionado.

[John]

bobsley:

Vou generalizar um pouco.

Se generalizarmos um pouco mais e tivermos em conta a situação real 1) DEVEMOS considerar swaps 2) Se exprimirmos SL e TP através de spread na sua fórmula, obtemos

p>= ( n_SL*spread + spread ) / (n_TP*spread + n_SL*spread) => p >= spread*(n_SL+1) / spread*(n_TP+n_SL) => p >= (n_SL+1)/(n_TP+n_SL)

Se o desenharmos como um gráfico, veremos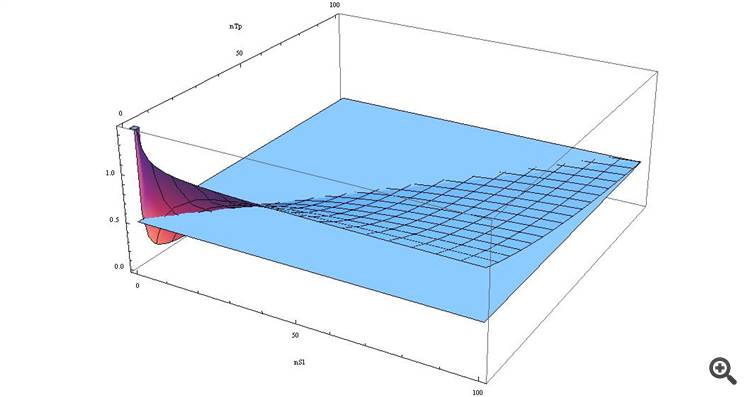

Vemos que com SL > TP a nossa função é superior a 0,5, e quanto mais próximos estes valores estão...

Aqueles que desejam ver por si próprios - aqui está a fórmula em termos da Wolfram-Alpha

g1 = Plot3D[(1 + nSl)/(nSl + nTp), {nSl, 0, 100}, {nTp, 0, 100}, AxesLabel -> Automatic]; 
g2 = Graphics3D[{Polygon[{{0, 0, 0.5}, {100, 0, 0.5}, {100, 100, 0.5}, {0, 100, 0.5}}], Polygon[{{0, 0, 0.9}, {100, 0, 0.9}, {100, 100, 0.9}, {0, 100, 0.9}}]}];
Show [{g1, g2}]

Uma conclusão inesperada para muitas pessoas, não é!)

Lembro-me há quanto tempo, aqui algumas pessoas gritaram - o que estou a dizer aqui, que "SL é maligno". :))

Por isso, agora os jovens apareceram e estão agora mais conhecedores. :)

[Mykola Demko]

bobsley:

Vamos generalizar um pouco.

Deixar sl (perda) e tp(lucro) serem fixados em pontos de moeda.

...

Se fizer alterações tais como um lote dinâmico, as coisas tornam-se consideravelmente mais complicadas e a probabilidade de um comércio lucrativo deve ser maior do que no caso acima mencionado.

Como uma fórmula puramente teórica, é claro que é interessante, mas!!!!

Se fizer mudanças como o lote dinâmico, tudo se torna muito mais complicado...

E se o lucro/perda não for fixo (mas diferente para todos os ofícios), tornar-se-á ainda mais complicado, e então adicionamos-lhe um spread flutuante - vamos ter uma tal confusão que 10 criadores de EA irão espalhá-lo por toda a tabela durante anos.

É por isso que tentei explicar que é difícil fazer o mercado funcionar com valores de take/loss fixo. Ao fixar o sistema subcotamos as asas do sistema (formalmente falando, ele não dá lucro).

E tp e sl como níveis fixos só são necessários para proteger a conta de perdas em caso de uma desconexão. Mas existem soluções mais simples do que a fixação.

Por exemplo, para paragens reais é suficiente estabelecer uma rede de arrasto de dois sentidos que se desloque para trás do mercado e nunca dispare enquanto houver uma ligação, e negociar de acordo com a situação.

Esta é a minha opinião.

[Avals]

MetaDriver:

Estão ambos errados :)

Na realidade, todas as moedas são tortas. É por isso que a Shannon tem razão. E eu também. ;)

Na realidade, as moedas alteram a sua curvatura à medida que são testadas). Porque não se pode repetir a experiência exactamente nas mesmas condições que a anterior. Os factores aleatórios mudam e pode bem acontecer que a sua curvatura resultante seja desequilibrada durante bastante tempo. Ou seja, trata-se da taxa de variação dos factores aleatórios em relação à experiência. Como o seu tempo interno se correlaciona com o tempo entre experiências.

Suponha, por exemplo, que um processo aleatório é gerado com base num único sinusoidal. Se na altura da experiência o valor do seno>0, então cabeças, menos do que isso - caudas. E então tudo dependerá da periodicidade das nossas experiências, precisão do cálculo do tempo e período de onda sinusoidal. Se os intervalos entre experiências não forem fixos e forem muito maiores do que o período da onda sinusoidal, então os valores aparecerão como aleatórios. Se o tempo entre experiências puder ser ajustado com uma precisão proporcional ao período da onda sinusoidal, a série não será determinística - até determinística (dependendo da precisão da medição do tempo).

Em geral, os processos aleatórios podem não ser periódicos, mas a sua ciclicidade e a soma de todos os factores aleatórios devem estar presentes. Por exemplo, não pode haver uma função continuamente crescente em vez de uma sinusoidal - então a série resultante terá uma tendência ascendente. Os processos aleatórios que afectam as séries são na realidade todos não aleatórios)))) só que não existe informação para medir com precisão a sua fase no momento da experiência, ou existe uma precisão de medição insuficiente.

Se a soma dos factores "aleatórios" for equilibrada em relação a 0 (como no exemplo com onda sinusoidal) - ou seja, se for acima de 0 e abaixo de 0, então a série sob a influência destes factores terá mo = 0. Se a soma for superior a 0 durante mais tempo, haverá um enviesamento a favor de cabeças ou a favor de caudas. Ou seja, a soma de factores aleatórios é, em certo sentido, equilibrada e cíclica. Só não sabemos o seu valor exacto na altura da experiência.

Mas a realidade é complicada pelo facto de os factores aleatórios poderem mudar e o mesmo se pode dizer da sua soma. Primeiro foi uma onda sinusoidal)) depois tornou-se uma linha recta num ângulo se nessas analogias. É por isso que a tarefa do comércio é apanhar tais momentos quando a série tem uma componente de tendência a subir ou a descer. Isto requer a correspondência com os processos subjacentes. Processos de retorno como padrões de retorno de forma sinusoidal (como o comércio plano), processos enviesados de derivação (tendência). Em geral, a tarefa é reconhecer um processo numa das suas fases, conhecendo a seguinte. A dificuldade é que existem muitos destes mini-processos e são de escala diferente, e com o tempo a sua influência muda simplesmente (amplitude se no quadro da analogia com uma onda sinusoidal).