Receitas para redes neurais

Introdução

Há não muito tempo - no alvorecer da análise técnica, quando de longe nem todos os traders tinham computadores - as pessoas pareciam tentar prever os preços futuros usando fórmulas e regularidades inventadas por eles mesmos. Eles eram chamados de charlatões com frequência. O tempo passou, os métodos de processamento de informação se tornaram mais complicados, e agora há poucos traders indiferentes à análise técnica. Qualquer trader iniciante pode facilmente utilizar gráficos, vários indicadores, buscar regularidades.

O número de traders da forex cresce diariamente. Com eles, suas exigências de métodos de análise de mercado crescem. Um dos métodos "relativamente" novos é o uso de redes neurais e de lógica fuzzy teoricamente. Vemos que os tópicos dedicados à essas questões são ativamente discutidos em vários fóruns temáticos. Eles existem, e continuarão existindo. Um humano que entrou no mercado dificilmente sairá dele. É o desafio à inteligência, ao cérebro e à força de vontade de uma pessoa. É por isso que um trader nunca para de estudar algo novo e usar várias abordagens na prática.

Neste artigo, analisaremos o básico da criação de redes neurais, aprenderemos sobre a noção de rede neural Kohonen e falaremos sobre os métodos de otimização de negociação. Este artigo é, antes de tudo, destinado aos traders que estão a recém iniciando os estudos e redes neurais e os princípios de processamento de informações.

Para cozinhar uma rede neural com a camada Kohonen é necessário:

1) 10.000 barras de histórico de qualquer par de moedas;
2) 5 gramas de médias em movimento (ou qualquer outro indicado - cabe a você);
3) de 2 a 3 camadas de distribuição inversa;
4) métodos de otimização como recheio;
5) os verdes do equilíbrio crescente e o número de direções de negociação acertadas.

Seção I. Receita para a camada Kohonen

Vamos começar a seção para aqueles que estão bem no início. Discutiremos várias abordagens para treinar a camada Kohonen ou, para ser mais preciso, sua versão básica, porque existem muitas variantes. Não há nada original neste capítulo, todas as explicações foram extraídas de referências clássicas deste tema. Entretanto, a vantagem deste capítulo é o grande número de imagens explicativas para cada seção.

Neste capítulo, trataremos das seguintes questões:
- a forma como os vetores de peso Kohonen são ajustados;
- a preparação preliminar da entrada de vetores;
- a seleção dos pesos iniciais dos neurônios Kohonen.

Então, segundo a Wikipédia, a rede neural Kohonen representa uma classe de redes neurais, o elemento principal sendo a camada Kohonen. A camada Kohonen consiste nos adicionadores lineares adaptativos ("neurônios formais lineares"). Como regra, os sinais de saída da camada Kohonen são processados de acordo com a regra "o vencedor levar tudo": os maiores sinais se tornam um só, todos os outros sinais viram zeros.

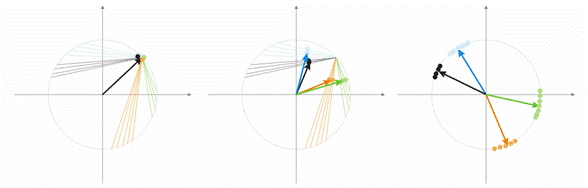
Agora, vamos discutir essa noção em um exemplo. Para fins de visualização, todos os cálculos serão dados para dois vetores de entrada dimensionais. Na fig. 1, o vetor de entrada é mostrado colorido. Cada neurônio da camada Kohonen (como de qualquer outra camada) simplesmente soma a entrada, multiplicando-a por seus pesos. Na verdade, todos os pesos da camada Kohonen são coordenadas de vetores deste neurônio.

Assim, a saída de cada neurônio Kohonen é o produto do ponto de dois vetores. Para a geometria, sabemos que o produto de ponto máximo será se o ângulo entre os vetores tender a zero (o ângulo cosseno tende a 1). Então, o valor máximo será o do neurônio da camada Kohonen que está mais próximo do vetor de entrada.

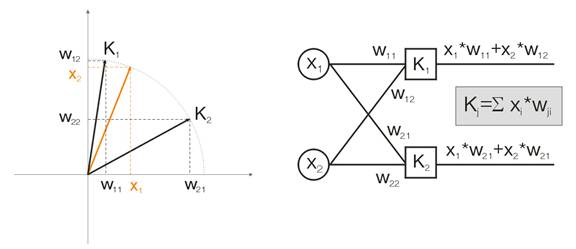
Fig. 1 O vencedor é o neurônio no qual o vetor é o mais próximo do sinal de entrada

Por definição, agora devemos encontrar o valor de saída máximo entre todos os neurônios, atribuir sua saída a um e atribuir zero a todos os outros neurônios. E a camada Kohonen nos "responderá" em qual área está o vetor de entrada.

Ajuste dos vetores de peso Kohonen

A finalidade do treinamento de camada, como escrito acima, é a classificação de espaço precisa dos vetores de entrada. Isso significa que cada neurônio deve ser responsável por sua área determinada, na qual está o vencedor. O erro de desvio do neurônio vencedor para o neurônio de entrada deve ser menor que o dos outros neurônios. Para atingir isso, o neurônio vencedor "se vira" no lado do vetor de entrada.
A Fig. 2 mostra a divisão dos neurônios (neurônios pretos) para dois vetores de entrada (coloridos).

Figura 2. Cada um dos neurônios aborda o sinal de entrada mais próximo

Com cada interação, o neurônio vencedor aborda "seu próprio" vetor de entrada. Suas novas coordenadas são calculadas de acordo com a seguinte fórmula:

em que A(t) é o parâmetro de velocidade de treinamento, dependendo do tempo t. Essa é uma função sem aumento que é reduzida a cada interação de 1 a 0. Se o valor inicial foi A=1, a correção de peso será feita em um estágio. Isso é possível quando, para cada vetor, há um neurônio Kohonen (por exemplo, 10 vetores de entrada e 10 neurônios na camada Kohonen).

Mas, na prática, tais casos quase nunca se encontram, porque normalmente o maior volume de dados de entrada precisa ser dividido em grupos de dados parecidos, diminuindo assim a diversidade de dados de entrada. É por isso que o valor de A=1 é indesejável. A prática mostra que o valor inicial ótimo deveria ser abaixo de 0,3.

Além disso, A é inversamente proporcional ao número de vetores de entrada. Isto é, em uma grande seleção, é melhor fazer pequenas correções, de forma que o neurônio vencedor não "navegar" por todo o espaço em suas correções. Como a funcionalidade A, normalmente qualquer função monotonamente diminuindo é escolhida. Por exemplo, diminuição linear ou hiperbólica, ou a função gaussiana.
A fig. 3 mostra a etapa de correção dos pesos de neurônio à velocidade A = 0,5. O neurônio aproximou o vetor de entrada, o erro é pequeno.

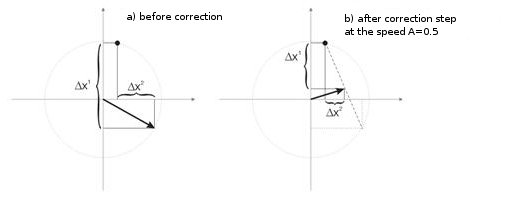
Figura 3. A correção do peso do neurônio está abaixo da influência do sinal de entrada

Pequeno número de neurônios em uma amostra ampla

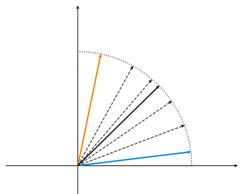
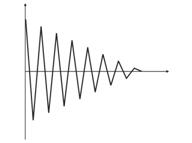
Figura 4. Os neurônios flutuam entre dois vetores de entrada

Na fig. 4 (esquerda), há dois vetores de entrada (coloridos) e apenas um neurônio Kohonen. No processo de correção, o neurônio balançará de um vetor para o outro (linhas pontilhadas). Como valor de A diminui até 0, ele estabiliza entre eles. As mudanças de coordenada do neurônio no tempo podem ser caracterizadas pela linha em ziguezague (direta da fig.4).

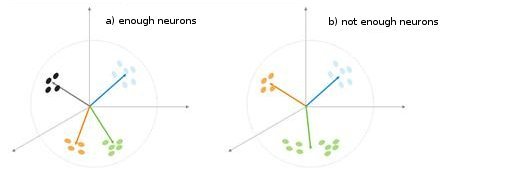
Fig. 5. A dependência do tipo de classificação nos números dos neurônios

Mais uma situação é mostrada na fig. 5. No primeiro caso, os quatro neurônios dividem adequadamente a amostra em quatro áreas de hiperesfera. No segundo caso, o número insuficiente de neurônios resulta no aumento de erro e na reclassificação da amostra. Assim, podemos concluir que a camada Kohonen deve conter o número suficiente de neurônios livres, o que depende do volume da amostra classificada.

Preparações preliminares de vetores de entrada
Como Philip D. Wasserman escreve em seu livro, é desejável (embora não obrigatório) normalizar os vetores de entrada antes de introduzi-los à rede. Isso é feito dividindo cada componente do vetor de entrada pelo comprimento de vetor. Esse comprimento é encontrado pela extração de uma raiz quadrada da soma das raízes dos componentes do vetor. Esta é a apresentação algébrica:

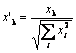
Ela transforma o vetor de entrada em um vetor único com a mesma direção, isto é, em um vetor com o comprimento da unidade no espaço de dimensão n. O significado dessa operação é claro - projetar todos os vetores de entrada na superfície da hiperesfera, simplificando assim a tarefa de busca da camada Kohonen. Em outras palavras, para estarmos procurando pelo ângulo entre os vetores de entrada e os neurônicos dos vetores Kohonen, devemos eliminar tal fator como o comprimento de vetor, igualando as chances de todos os neurônios.

Com frequência, elementos de vetores de amostra são valores não negativos (por exemplo, valores de médias em movimento, preço). Todos eles estão concentrados no espaço do quadrante positivo. Como resultado de normalização de uma amostra "positiva", obtemos um grande acúmulo de vetores em apenas uma área positiva, o que não é muito bom para a qualificação. É por isso que, antes da normalização, o nivelamento da mostra pode ser feito. Se a amostra for um tanto grande, podemos assumir que os vetores estão localizados aproximadamente em uma área sem "intrusos" que estejam longe da amostra principal. Assim, uma amostra pode ser central em relação a suas coordenadas "extremas".

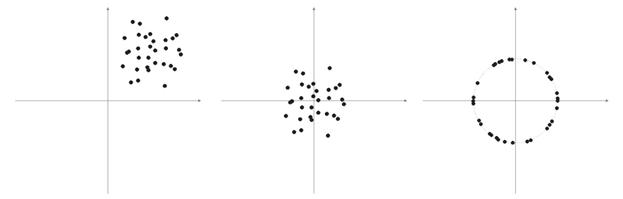
Fig. 6. Normalização de vetores de entrada

Como escrito acima, a normalização de vetores é desejável. Ela simplifica a correção da camada Kohonen. Entretanto, devemos representar com clareza uma amostra e decidir se ela deve ser projetada em uma esfera ou não.

Listagem 1. Estreitamento de vetores de entrada na faixa [-1, 1]

for (N=0; N<nNeuron[0]; N++) // for all neurons of the input layer
 {
  min=in[N][0]; // finding minimum in the whole sample
  for (pat=0; pat<nPattern; pat++) if (in[N][pat]<min) min=in[N][pat];
  for (pat=0; pat<nPattern; pat++) in[N][pat]-=min; // shift by the value of the minimal value 
  max=in[N][0]; // finding maximum in the whole sample
  for (pat=0; pat<nPattern; pat++) if (in[N][pat]>max) max=in[N][pat];
  for (pat=0; pat<nPattern; pat++) in[N][pat]=2*(in[N][pat]/max)-1; // narrowing till [-1,1]
 }

Se normalizarmos os vetores de entrada, devemos normalizar de forma correspondente todos os pesos de neurônios.


Como selecionar os pesos de neurônio inicial
Variantes possíveis são neurônios.
1) Valores aleatórios são atribuídos aos pesos, como é feito normalmente com os neurônios (randomizando);
2) A inicialização por exemplos, quando os valores de exemplos selecionados aleatoriamente de uma amostra de teste são designados como valores iniciais;
3) Inicialização linear. Neste caso, os pesos são iniciados pelos valores de vetor que são ordenados linearmente ao longo de todo o espaço linear localizado entre dois vetores do conjunto inicial de dados;
4) Todos os pesos têm os mesmos valores - método de combinação convexa.

Vamos analisar o primeiro e o último casos.
1) Valores aleatórios são designados aos pesos.

Durante a randomização, todos os neurônios de vetores são distribuídos na superfície de uma hiperesfera. Enquanto os vetores de entrada têm uma tendência de agrupamento. Neste caso, pode acontecer de alguns vetores de pesos serem tão distantes dos vetores de entrada que nunca poderão ter uma correlação melhor e, consequentemente, não poderão aprender - figuras em "cinza" na fig. 7 (direita). Além disso, os neurônios restantes não serão suficientes para minimizar o erro e dividir classes parecidas - a classe "vermelha" está incluída no neurônio "verde".

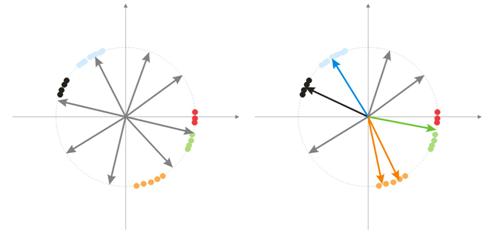
Fig. 7. Resultado do treinamento dos neurônios randomizados

E se houver um grande acúmulo de neurônios em uma área, vários neurônios podem entrar na área de uma classe e dividi-la em subclasses - área laranja na fig. 7. Isso não é crítico, porque o processamento adicional de sinais de camada pode concertar a situação mas isso demora o tempo do treinamento.

Uma das variantes para resolver esses problemas é o método quando a correção é feita nos estágios inicial não só nos vetores de um neurônio vencedor, mas também no grupo de vetores mais próximos. Depois, o número do grupo diminui gradualmente e por fim apenas um neurônio é corrigido. Um grupo pode ser selecionado de uma série ordenada de saídas de neurônio. Os neurônios das primeiras saídas máximas K serão corrigidos.

Uma outra abordagem no grupo de ajuste do peso de vetores é o seguinte método.

a) Para cada neurônio, o comprimento do vetor de correção é definido:

.
b) Um neurônio com a distância mínima se torna um vencedor - Wn. Após um grupo de neurônios ser encontrado, a correção sobre qual está no limite da distância C*Ln de Wn.
c) Os pesos desses neurônios são corrigidos por uma regra simples . Assim, a correção de toda a amostra é feita.

O parâmetro C muda no processo de treinamento de algum número (normalmente de 1) para 0.

O terceiro método interessante implica que cada neurônio pode ser corrigido apenas N/k vezes para um passando pela amostra. Aqui, N é o tamanho da amostra, k - o número de neurônios. Isto é, se quaisquer neurônios se tornarem vencedores com mais frequência que outros, ele "termina o jogo" até o final da passagem pela amostra. Assim, outros neurônios também podem aprender.

2) método de combinação convexa

O significado do método implica que os vetores de peso e de entrada estão colocados inicialmente em uma área. Fórmulas do cálculo de coordenadas atuais de vetores de entrada e de peso inicial serão as seguintes:

,

em que n é a dimensão de um vetor de entrada, a(t)- função não decrescente no tempo, com cada interação aumentando seu valor de 0 a 1, como resultado de que todos os vetores de entrada coincidem com os vetores de saída e finalmente pegam seus lugares. Além disso, os vetores de peso estarão "alcançando" suas classes.

Isso é tudo material sobre a versão básica da camada Kohonen que será aplicada nesta rede neural.

II. Colheres, conchas e scripts

O primeiro script que vamos discutir reunirá os dados em barras e criará um arquivo de vetores de entrada. Como um exemplo de treinamento, vamos usar MA.

Listagem 2. Como criar um arquivo de vetores de entrada

// input parameters
 #define NUM_BAR 10000 // number of bars for training (number of training patterns)
 #define NUM_MA 5 // number of movings
 #define DEPTH_MA 3 // number of values of a moving
 // creating a file
 hFile = FileOpen(FileName, FILE_WRITE|FILE_CSV);
 FileSeek(hFile, 0, SEEK_END); 
 // Creating an array of inputs
 int i, ma, depth;
 double MaIn;
 for (i=NUM_BAR; i>0; i--) // going through bars and collecting values of MA fan 
 {
  for (depth=0; depth<DEPTH_MA; depth++) //calculating moving values
   for (ma=0; ma<NUM_MA; ma++) 
   {
   MaIn=iMA(NULL, 0, 2+MathSqrt(ma*ma*ma)*3, 0, 1, 4, 
                    i+depth*depth)- ((High[i+depth*depth] + Low[i+depth*depth])/2);
   FileWriteDouble(hFile, MaIn);
   }
  }

O arquivo de dados é criado como o meio de transmissão de informações entre os aplicativos. Quando você estiver conhecendo algoritmos de treinamento, é fortemente recomendado que assista aos resultados provisórios da operação, os valores de algumas variáveis e, se necessário, alterar as condições de treinamento.

É por isso que recomendamos que você use a linguagem de programação de nível alto (VB, VC++ etc.), enquanto os meios de depuração atuais de MQL4 não são suficientes (espero que essa situação seja melhorada no MQL5). Depois, quando você aprender todas as armadilhas dos seus algoritmos e funções, poderá começar a usar o MQL4. Além disso, você terá que escrever o alvo final (indicador ou Expert Advisor) em MQL4.

Estrutura generalizada de classes

Listagem 3. Classe de rede neural

class CNeuroNet : public CObject  
 {
 public:
  int nCycle; // number of learning cycles until stop
  int nPattern; // number of training patterns
  int nLayer; // number of training layers
  double Delta; // required minimal output error
  int nNeuron[iMaxLayer]; // number of neurons in a layer (by layers)
  int LayerType[iMaxLayer]; // types of layers (by layers)
  double W[iMaxLayer][iMaxNeuron][iMaxNeuron];// weights by layers
  double dW[iMaxLayer][iMaxNeuron][iMaxNeuron];// correction of weight
  double Thresh[iMaxLayer][iMaxNeuron]; // threshold
  double dThresh[iMaxLayer][iMaxNeuron]; // correction of threshold
  double Out[iMaxLayer][iMaxNeuron]; // output value
  double OutArr[iMaxNeuron]; // sorted output values of Kohonen layer
  int IndexWin[iMaxNeuron]; // sorted neuron indexes of Kohonen layer
  double Err[iMaxLayer][iMaxNeuron][iMaxNeuron];// error

  double Speed; // Speed of training
  double Impuls; // Impulse of training

  double in[100][iMaxPattern]; // Vector of input values
  double out[10][iMaxPattern]; // vector of output values
  double pout[10]; // previous vector of output values
  double bar[4][iMaxPattern]; // bars, on which we learn
  int TradePos; // order direction
  double ProfitPos; // obtained profit/loss of an order

 public:
  CNeuroNet();
  virtual ~CNeuroNet();
  // functions
  void Init(int aPattern=1, int aLayer=1, int aCycle=10000, double aDelta=0.01, double aSpeed=0.1, 
                                                                               double aImpuls=0.1);
  // learning functions
  void CalculateLayer(); // Calculation of layer output
  void CalculateError(); // Error calculation /for Target array/
  void ChangeWeight(); // Correction of weights
  bool TrainNetwork(); // Network training
  void CalculateLayer(int L); // Output calculation of Kohonen layer
  void CalculateError(int L); // Error calculation of Kohonen layer
  void ChangeWeight(int L); // Correction of weights for layer indication
  bool TrainNetwork(int L); // Training of Kohonen layer

  bool TrainMPS(); // Network training for getting the best profit

  // variables for internal interchange
  bool bInProc; // flag for entering the TrainNetwork function
  bool bStop; // flag for the forced termination of the TrainNetwork function
  int loop; // number of the current iteration
  int pat; // number of the current processed pattern
  int iMaxErr; // pattern with the maximal error
  double dMaxErr; // maximal error
  double sErr; // square of pattern error
  int iNeuron; // maximal number of neurons in Kohonen layer correction
  int iWinNeuron; // number of winner neurons in Kohonen layer

  int WinNeuron[iMaxNeuron]; // array of active neurons (ordered)
  int NeuroPat[iMaxPattern][iMaxNeuron]; // array of active neurons

  void LinearCovariation(); // normalization of the sample
  void SaveW(); // Analysis of neuron activity
 };

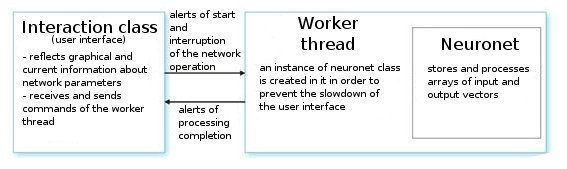
Na verdade, a classe não é complexa. Ela contém o conjunto necessário principal + variáveis de serviço.

Vamos analisá-la. Após o comando de um usuário, a classe de interface cria um segmento de rede e inicializa um temporizador para a leitura periódica dos valores de rede. Ela também recebe índices para ler informações dos parâmetros de redes neurais. O segmento de trabalho por sua vez lê as séries de vetores de entrada/saída do arquivo preparado preliminarmente e define os parâmetros das camadas (tipos de camadas e números de neurônios em cada camada). Esse é o estágio de preparação.

Depois disso, chamamos a função CNeuroNet::Init, na qual os pesos são inicializados, a amostra é normalizada e os parâmetros de treinamento são definidos (velocidade, impulso, erro exigido e número de ciclos de treinamento). E somente após chamarmos a função "burro de carga" - CNeuroNet::TrainNetwork (ou TrainMPS, ou TrainNetwork(int L), dependendo do que quisermos obter). Quando o treinamento terminar, o segmento de trabalho salva os pesos de rede em um arquivo para a implementação do último em um indicador ou no Expert Advisor.

III. Assando a rede

Agora, vamos aos problemas de treinamento. A prática usual no treinamento é definir o par "professor-padrão". Ou seja, um certo alvo corresponde a cada padrão de entrada. A base de diferença entre a entrada atual e a correção de valor alvo de pesos é executada. Por exemplo, um pesquisador quer que a rede preveja o preço da barra seguinte na base de preços das últimas 10 barras apresentadas à rede. Nesse caso, após colocar os valores de 10 entradas, precisamos comparar a saída obtida e o valor de professor e depois corrigir os pesos para a diferença entre eles.

No modelo que oferecemos, não há vetores "professor" no sentido usual, porque não sabemos de antemão em que barras devemos entrar ou sair do mercado. Isso significa que nossa rede corrigirá seus vetores de saída com base em seus próprios valores de saída. Isso significa que a rede tentará obter o lucro máximo (maximização do número de direções de negociação previstas corretamente). Vamos considerar um exemplo da fig. 8.

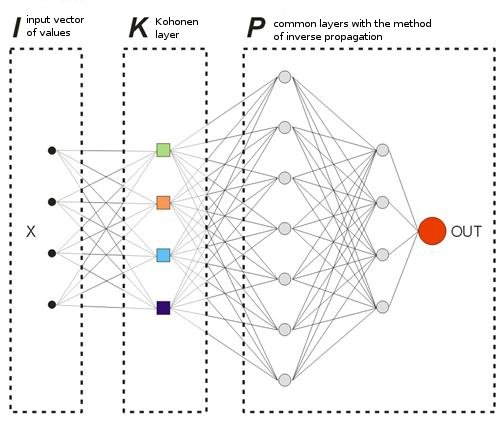
Fig. 8. Esquema de uma rede neural treinada

A camada Kohonen que é pré-treinada em uma amostra avança seu vetor para mais perto da rede. Na saída da última camada da rede, teremos o valor OUT, que é interpretado da seguinte forma. Se OUT>0,5, insira um Buy; se OUT<0,5, insira um Sell (os valores sigmoides são alterados nos limites [0, 1]).

Suponha que para algum vetor de entrada X1 a rede responde pela saída OUT1>0,5. Isso significa que na barra a qual o padrão pertence abrimos uma posição Buy. Depois disso, na apresentação cronológica dos vetores de entrada em alguns Xk o sinal OUTk se transforma no "oposto". Consequentemente, fechamos a posição Buy e abrimos a posição Sell.

Exatamente nesse momento, precisamos ver o resultado da ordem fechada. Se obtivermos lucro, podemos fortalecer esse alerta. Ou podemos considerar que não há nenhum erro e não corrigiremos nada. Se tivermos perdas, corrigimos os pesos das camadas de tal forma que a inserção pelo alerta do vetor X1 que mostra OUT1<0,5.

Agora, vamos calcular o valor de uma saída de professor (alvo). Como tal, vamos pegar o valor de um sigmoide da perda obtida (em pontos) multiplicado pelo sinal da direção de negociação. Consequentemente, quanto maior a perda, mais rigorosa será a forma como a rede será punida e corrigira seus pesos pelo maior valor. Por exemplo, se tivermos que os pontos de perda = 50 em Buy, a correção da camada de entrada será calculada como mostrado abaixo:

, ,

Podemos delimitar as regras de negociação introduzindo no processo de análise de negociação os parâmetros de TakeProfit (TP) e StopLoss (SL) em pontos. Então, precisamos traçar 3 eventos: 1) mudança do sinal OUT , 2) mudanças de preço do preço aberto para o valor de TP, 3) mudanças de preço do preço aberto pelo valor de -SL.

Quando um desses eventos ocorrer, a correção de pesos será feita de forma análoga. Se obtivermos lucro, os pesos permanecerão inalterados ou serão corrigidos (sinal mais forte). Se tivermos perda, os pesos serão corrigidos para fazer a entrada pelo alerta do vetor X1 mostrar OUT1 com o sinal "desejado".

A única desvantagem dessa limitação é o fato de que usamos os valores absolutos TP e SL, o que não é tão bom para a otimização de uma rede em um longo período de tempo nas condições atuais do mercado. Quanto ao meu aviso, TP e SL não devem diferenciar muito um do outro.

Isso significa que o sistema deve ser simétrico para evitar o desvio na direção de uma tendência mais global de Buy ou Sell durante o treinamento. Também há a opção de que o TP deve ser de 2 a 4 vezes maior que o SL - assim, aumentamos de forma artificial a razão de negociações rentáveis e de perda. Mas, em tal caso, arriscamos o treinamento da rede com uma alteração em direção a tendência. Claro, essas duas variantes podem existir, mas você deve verificar ambas em suas investigações.

Listagem 4. Uma interação da configuração de peso de rede

int TradePos;
 int pat=0; // open an order for the first pattern
 for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // take the training pattern
 CalculateLayer(); // calculate the network output
 TradePos=TradeDir(Out[nLayer-1][0]); // if exit is larger than 0.5, then buy. Otherwise - sell
 ipat=pat; // remember the pattern
 for(pat=1;pat<nPattern;pat++) // go through the pattern and train the network
 {
  for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // take the training pattern
  CalculateLayer(); // calculate the network output
  ProfitPos=1e4*TradePos*(bar[3][pat]-bar[3][ipat]); // calculate profit/loss at close prices [3]
  // if trade direction has changed or stop order has triggered
  if (TradeDir(Out[nLayer-1][0])!=TradePos || ProfitPos>=TP || ProfitPos<=-SL) 
  {
   // correcting weights
   Out[nLayer][0]=Sigmoid(0.1*TradePos*ProfitPos); // set the desired output of the network
   for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][ipat];// take the pattern by which
                                                   // CalculateLayer() were opened;  
                                                   // calculate the network output
   CalculateError(); // calculate the error
   ChangeWeight(); // correct weights
   for(i=0;i<nNeuron[0];i++) Out[0][i]=in[i][pat]; // go to the new order CalculateLayer(); 
                                                   // calculate the new output of the network
   TradePos=TradeDir(Out[nLayer-1][0]);            // if output is > 0.5, then buy 
                                                   //otherwise sell ipat=pat; 
                                                   // remember the pattern
  }
 }

Com esses passos simples, a rede finalmente distribuíra as classes obtidas da camada Kohonen de tal forma que haverá um alerta de entrada no mercado com o número máximo de lucros correspondente a cada uma. Do ponto de vista da estatística - cada padrão de entrada é ajustado pela rede para o trabalho em grupo.

Enquanto um e o mesmo vetor de entrada pode dar alertas em diferentes direções durante o processo de ajuste de pesos, obtendo gradualmente o número máximo de previsões verdadeira, esse método pode ser chamado de dinâmico. O método usado é conhecido como MPS - Sistema de maximização de lucro.

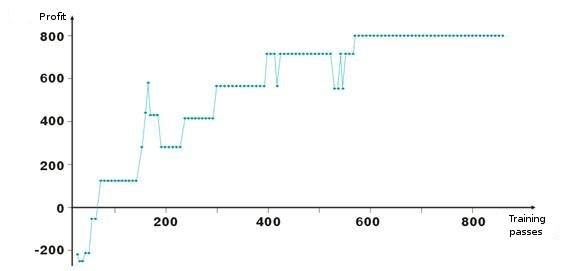
Aqui estão os resultados de ajuste de peso de rede. Cada ponto no gráfico é o valor de um lucro obtido em pontos durante uma passagem de período de treinamento. O sistema está sempre no mercado, TakeProfit = StopLoss = 50 pontos, o conserto é feito apenas por uma ordem de parada, os pesos são corrigidos em caso de lucro e perda.

Veja, após os pesos de início negativo das camadas serem ajustados de forma que próximo da centésima interação o lucro se torna positivos. O interessante é que o sistema meio que desacelera em alguns níveis. Isso está conectado aos parâmetros de velocidade de treinamento.

Como pode ser visto na listagem 2, o lucro ProfitPos é calculado pelos preços próximos de uma barra, na qual entramos, e na qual uma das condições foi atingida (ordem de parada ou alteração de alerta). Claro, este é um método duro, especialmente no caso de ordens de parada. Podemos adicionar uma complicação ao analisar os preços High e Low de uma barra (bar[1][ipat] e bar[2][ipat] correspondentemente). Tente você mesmo.

Trocar ou buscar entradas?
Então, estudamos o método dinâmico de treinamento que treina a rede com seus próprios erros. Você deve ter notado que de acordo com o algoritmo estamos sempre no mercado, consertando lucro/perda e continuando. Então, precisamos delimitar nossas entradas e tentar entrar no mercado somente em vetores de entrada "favoráveis". Isso significa que precisamos definir a dependência do nível do alerta de entrada de rede no número de negociações rentáveis/de perda.

Isso pode ser feito de forma bem simples. Vamos introduzir a variável 0<M0,5+M, então compre, se Out<0,5-M, então venda. Percorremos as entradas e saídas naqueles vetores que ficam entre 0,5-M<Out<0,5+M.

Outro método para percorrer vetores desnecessários é juntar as informações estatísticas sobre a rentabilidade de uma ordem de valores de certas entradas de rede. Vamos chamá-lo de análise virtual. Antes disso, devemos definir o método de fechamento de posição - alcance da ordem de parada, alteração do sinal de entrada de rede. Então vamos criar uma tabela Out | ProfitPos. Os valores de Out e ProfitPos são calculados para cada vetor de entrada (isto é, para cada barra).

Então, vamos fazer a tabela de resumo do campo ProfitPos. Como resultado, veremos a dependência do valor Out e do lucro obtido. Selecione a faixa Out=[MLo, MHi], na qual temos o melhor lucro e usamos seus valores na negociação.

De volta ao MQL4
Tendo começado o desenvolvimento em VC++, não tentamos depreciar as possibilidades do MQL4. Isso se deu pela conveniência. Conterei sobre um incidente. Recentemente, um dos meus conhecidos tentou obter uma base de empresas na nossa cidade. Há vários diretórios na Internet, mas ninguém queria vender a base.

E escrevemos um script em MQL4 que escaneia uma página html e seleciona uma área com informações sobre a empresa, e depois a salva em um arquivo. Depois, editamos o arquivo em Excel e a base de dados de três páginas amarelas grandes com todos os números de telefone, endereços e atividades da empresa estava pronta. Essa era a base de dados mais completa da cidade; para mim, o sentimento foi de orgulho pela facilidade e pelas possibilidades do MQL4.

Naturalmente, é possível lidar com uma tarefa em linguagens diferentes, mas é melhor selecionar aquela que será ótima em termos de razão de possibilidade/dificuldade para uma determinada tarefa.

Então, após o treinamento da rede, devemos salvar todos os seus parâmetros em um arquivo para transferi-los em MQL4.
- tamanho do vetor de entrada
- tamanho do vetor de saída
- número de camadas
- número de neurônios por camadas - de entrada para saída
- pesos de neurônios por camadas
O indicador usará apenas uma função do arsenal de classe CNeuroNet – CalculateLayer. Vamos formar um vetor de entrada para cada barra, calcular o valor da saída de rede e construir o indicador [6].

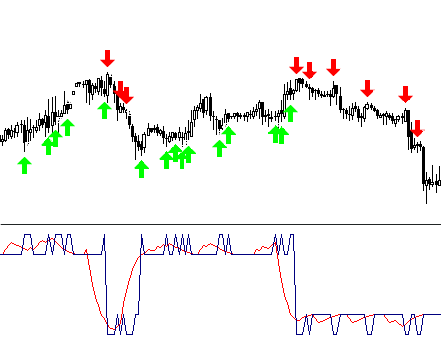
Se já tivermos decidido em níveis de entrada, podemos pintar as partes da curva obtida de cores diferentes.
O exemplo do código !NeuroInd.mq4 está anexado ao artigo.

IV. Abordagem criativa

Para uma boa implementação, devemos ter uma mente ampla. Redes neurais não são exceção. Não acho que a variante oferecida seja ideal e adequada a qualquer tarefa. É por isso que você sempre deve pesquisar suas próprias soluções, desenhar a figura geral, sistematizar e verificar ideias. Abaixo, você encontrará alguns avisos e recomendações.
- Adaptação da rede. Uma rede neural é um aproximador. Uma rede neural restaura uma curva quando ela obtém pontos nodais. Se a quantidade de pontos for muito grande, a construção no futuro trará resultados ruins. Dados de história antiga devem ser removidos do treinamento e novos devem ser adicionados. É assim que a aproximação de um novo polinomial é feita.
- Treinamento excessivo. Ele ocorre no ajuste "ideal" (ou durante o treinamento de uma rede, os barulhos dos valores de entrada. Como resultado, quando um valor teste é dado a uma rede, ela mostrará o resultado errado (fig.9).

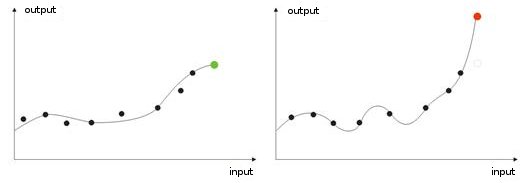
Fig. 9. Resultado de uma rede com "treinamento excessivo" - previsão errada

- Complexidade, repetição, inconsistência de um treinamento simples. Em trabalhos [8, 9], autores analisam a dependência entre os parâmetros numerados. Acredito estar claro que se diferentes vetores professores (ou, caso seja pior, contraditórios) corresponderem ao mesmo vetor de aprendizagem, uma rede nunca aprenderá a classificá-los corretamente. Para este fim, vetores de entrada grandes devem ser criados, para que contenham os dados que permitirão delimitá-los no espaço de classes. A fig. 10 mostra essa dependência. Quanto mais alta a complexidade de um vetor, mais baixa será a repetibilidade e a inconsistência dos padrões.

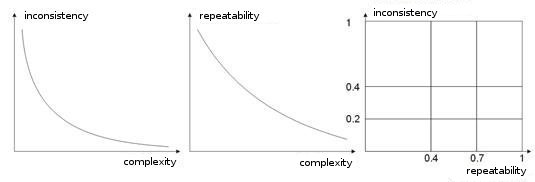
Fig. 10. Dependência de características de vetores de entrada

- Treinamento de rede pelo método Boltzmann. Esse método é parecido com a tentativa de várias variantes de peso possíveis. O Expert Advisor ArtificialIntelligence funciona de acordo ao princípio similar em seu aprendizado. Ao treinar uma rede, ela passa por absolutamente todas as variantes de valores de peso (como decifrar a senha de uma conta de e-mail) e seleciona a melhor combinação.

Essa é uma tarefa de trabalho intenso para um computador, e é por isso que o número de todos os pesos de uma rede é limitado por dez. Por exemplo, e o peso se altera de 0 a 1 na etapa 0,01, precisaremos de 100 etapas. Para 5 pesos, isso significa 5.100 combinações. Esse é um número grande e essa tarefa está além do poder de um computador. A única forma de construir uma rede por esse método é usar um número grande de computadores, cada um processando determinada parte.

Essa tarefa pode ser realizada por 10 computadores. Cada um processará 510 combinações, então uma rede pode ser feita mais complexa usando um número grande de pesos, camadas e etapas.

De forma distinta de um "Ataque com força bruta", o método de Boltzmann age mais suavize e mais rápido. A cada interação, uma mudança aleatória sobre o peso é definida. Se com o novo peso o sistema melhorar suas características de entrada, o peso é aceito e uma nova interação é feita.

Se o peso aumenta o erro de entrada, ele é aceito com a probabilidade calculada pela fórmula de distribuição de Boltzmann. Assim, no início, a entrada de rede pode ter absolutamente valores diferentes, "esfriando" gradualmente e trazendo a rede para o mínimo global exigido [10, 11].

Claro, essa não é a lista completa de estudos adicionais, há também algoritmos genéticos, métodos para melhorar a convergência, redes com memória, redes radicais, máquinas de associação etc.

Conclusão

Gostaria de adicionar que uma rede neural não é uma cura universal para todos os seus problemas de negociação. Quando alguém seleciona o trabalho independente e a criação de seu próprio algoritmo, outra pessoa preferiria usar pacotes de neurônios prontos, grandes números os quais podem ser encontrados no mercado.

É só não ter medo de fazer experiências! Boa sorte e que você tenha bons lucros!

O mercado é um intelecto, o portfólio financeiro é uma rede neural.

Referências

1. Baestaens, Dirk-Emma; Van Den Bergh, Willem Max; Wood, Douglas. Neural Network Solutions for Trading in Financial Markets.
2. Voronovskii G.K. e outros. Geneticheskie algoritmy, iskusstvennye neironnye seti i problemy virtualnoy realnosti (Genetic Algoritms, Artificial Neural Networks and Problems of Virtual Reality).
3. Galushkin A.I. Teoriya Neironnyh setei (Theory of Neural Networks).
4. Debok G., Kohonen T. Analyzing Financial Data using Self-Organizing Maps.
5. Ezhov A.A., Shumckii S.A. Neirokompyuting i ego primeneniya v ekonomike i biznese (Neural Computing and Its Use in Economics and Business).
6. Ivanov D.V. Prognozirovanie finansovyh rynkov s ispolzovaniem neironnyh setei (Forcasring of Financial Maarkets Using Artificial Neural Networks) (Graduate work).
7. Osovsky S. Neural Networks for Data Processing.
8. Tarasenko R.A., Krisilov V.A., Vybor razmera opisaniya situatsii pri formirovanii obuchayushchey vyborki dlya neironnyh setei v zadachah prognozirovaniya vremennyh ryadov (Choosing the Situation Discription Size when Forming a Training Sample for Neural Networks in Tasks of Forecasting of Time Series).
9. Tarasenko R.A., Krisilov V.A., Predvaritelnaya otsenka kachestva obuchayushchey vyborki dlya neironnyh setei v zadachah prognozirovaniya vremennyh ryadov (Preliminaruy Estimation of the Quality of a training Sample for Neural Networks in Tasks of Forecasting of Time Series).
10. Philip D. Wasserman. Neral Computing: Theory and Practice.
11. Simon Haykin. Neural Networks: A Comprehensive Foundation.
12. www.wikipedia.org
13. The Internet.