
Teoria das Categorias em MQL5 (Parte 2)
Introdução
Esta é uma continuação do artigo anterior no uso da Teoria das Categorias em MQL5. Apenas para recapitular, nós apresentamos a teoria das categorias como um ramo da matemática particularmente útil para organizar e classificar as informações. Nesse contexto, nós discutimos alguns conceitos básicos da teoria das categorias e como ela pode ser aplicada à análise de dados das séries temporais financeiras. Especificamente, nós examinamos os elementos, domínios e morfismos. Os elementos são as unidades básicas de informação dentro de um sistema da teoria das categorias, e são tipicamente pensados como membros de um conjunto, referido nesta série, como um domínio. Um domínio pode ter relacionamentos com outros domínios por meio de um processo chamado morfismo. Para este artigo, nós começaremos abordando o que constitui uma categoria, observando os axiomas de identidade e associação, diagrama comutativo. Ao fazer isso, e ao longo do artigo, nós examinaremos os exemplos e também destacaremos os exemplos de não categorias. Por fim, nós concluiremos apresentando os logs da ontologia.
Antes de nos aprofundarmos nas definições de axiomas de uma categoria, pode ser útil examinar alguns exemplos cotidianos de categorias "em ação". Já definimos os domínios e os elementos que eles contêm. Portanto, para começar nós consideramos uma categoria como uma coleção de domínios relacionados, os exemplos a seguir podem servir como exemplos ilustrativos.
- Uma categoria de tipos de transporte, com domínios que representam diferentes modos de transporte (por exemplo, carros, aviões e trens, etc.). Os elementos de cada domínio seriam os respectivos tipos de veículos de transporte. Por exemplo, em carros, nós poderíamos ter o compartilhamento de carona, aluguel de carro, carro pessoal, táxi; enquanto nos aviões nós poderíamos ter jatos particulares, aviões comerciais e alugados; com trens poderíamos ter bondes, trem-bala, locomotivas a vapor etc. O morfismo entre eles poderia então servir para definir um itinerário de viagem completo. Por exemplo, se você pegou um lyft para o aeroporto, voo comercial e, em seguida, pegou um trem-bala desse aeroporto para o seu destino, cada uma dessas opções pode ser mapeada facilmente dentro desta categoria.
- Uma categoria de cursos de uma refeição, com domínios representando menus para cada curso. Digamos que nós temos 5 pratos, a saber: entrada, sopa, prato principal, sobremesa e queijo. Nesse caso, os elementos de cada domínio seriam os alimentos do cardápio do respectivo curso. Por exemplo, o prato do aperitivo poderia ter em seu domínio (menu) opções compostas por: cenouras cristalizadas com mel, cominho e páprica; OU cogumelos recheados com pecorino romano, alho e pão ralado; OU brócolis na brasa com pimentão shishito e cebola em conserva; Da mesma forma, o domínio da sopa poderia ter: feijão branco toscano e sopa de alho assado; OU bisque de abóbora e sálvia; OU sopa fria de melão e manjericão. Cada um desses itens de menu representa um elemento em seu domínio. Da mesma forma, o morfismo entre eles servirá para definir uma refeição completa escolhida por um cliente do restaurante. Por exemplo, se o cliente tiver cenouras cristalizadas, depois abóbora e assim por diante para todos os outros pratos, cada uma dessas opções acima pode ser mapeada facilmente dentro da categoria.
- Outro exemplo de categoria pode ser os tipos de entretenimento semanal. Aqui, nossos domínios podem ser esportes ao vivo, streaming de TV e visitas a parques. Os elementos de cada domínio podem ser: NFL, MLB ou NBA para o domínio de esportes ao vivo; Netflix ou HBO ou AMC para domínio de streaming de TV; e Disney ou zoológico ou parque natural para as visitas ao parque. Mais uma vez, o público pode selecionar em cada domínio um jogo esportivo para assistir, um programa de TV para assistir e um parque para visitar. E a sequência de seleções nesses domínios (morfismos) permite facilmente que essas informações sejam mapeadas.
Portanto, tudo isso, e obviamente muito mais, pode ser registrado pela Teoria das categorias. Mas para quê? Há um ditado que diz "um mau trabalhador culpa suas ferramentas" e acho que esse é o ponto aqui. Pois o uso é realmente determinado pelo usuário. Na minha opinião, a Teoria das Categorias serve criticamente para quantificar equivalência. Este é um tópico que abordaremos em outros artigos depois de cobrirmos alguns conceitos básicos. Basta dizer que é a razão pela qual duas categorias separadas em tópicos diferentes que podem parecer não relacionados na superfície, mas em uma inspeção mais profunda são descobertas como idênticas ou opostas espelhadas. Esses insights são vitais na tomada de decisões porque raramente você tem informações suficientes no momento de tomar decisões. Se, no entanto, você tiver categorias correlatas, a lacuna de informações poderá ser preenchida.
Identidade
Isomorfismo é uma propriedade crucial dos homomorfismos na teoria das categorias porque garante que a estrutura dos domínios na categoria de destino seja preservada sob o mapeamento. Também garante a preservação das operações algébricas dos domínios na categoria de origem. Por exemplo, vamos considerar uma categoria de vestuário onde os domínios são camisas e calças, e os morfismos são as funções que mapeiam o tamanho de uma camisa para o tamanho de uma calça. Um homomorfismo nesta categoria seria uma função que preserva o pareamento dos tamanhos das camisas aos respectivos tamanhos das calças. Um isomorfismo nessa categoria seria uma função que não apenas preserva o pareamento algébrico dos tamanhos, mas também estabelece uma correspondência biunívoca entre os tamanhos das camisas e das calças. Isso significa que, para qualquer tamanho de camisa, há exatamente um tamanho de calça correspondente e vice-versa. Por exemplo, considere a função que mapeia o tamanho de uma camisa (por exemplo, "pequeno", "médio", "grande") para o tamanho de uma calça (por exemplo, "26", "28", "30", "32"). Esta função é um homomorfismo porque preserva e define um emparelhamento dos tamanhos (por exemplo, "pequeno" pode ser emparelhado com "26"). Mas não é um isomorfismo porque não estabelece uma correspondência biunívoca entre os tamanhos das camisas e das calças, visto que o "pequeno" também pode ser usado com "28" ou "26". Não há reversibilidade.
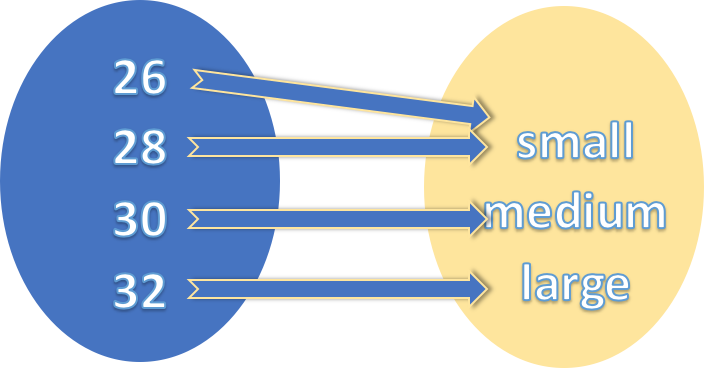
Por outro lado, considere a função que mapeia o tamanho de uma camisa (por exemplo, "pequeno", "médio", "grande") apenas para os tamanhos de uma calça (por exemplo, "28", "30", "32") . Esta função não é apenas um homomorfismo, mas também um isomorfismo porque também permite a reversibilidade.
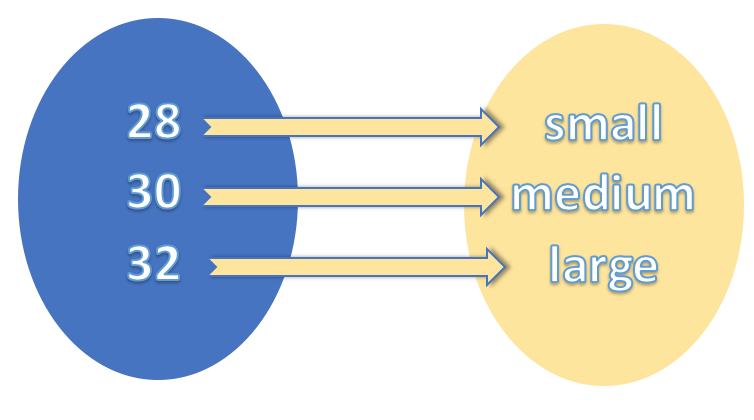
No exemplo de uma categoria de vestuário, onde os domínios são camisas e calças, e os morfismos são as funções que mapeiam o tamanho de uma camisa para o tamanho de uma calça, um único morfismo não pode ser isomórfico porque todos os morfismos individuais são inerentemente reversíveis ao 'isomorfismo'. A propriedade do isomorfismo lida com um grupo de morfismos (também conhecido como conjunto de homomorfismo) de um domínio para um contradomínio e só pode ser considerado presente se todos esses morfismos como um grupo puderem ser revertidos, preservando as propriedades de emparelhamento algébrico do homomorfismo. É por isso que é importante enumerar todos os morfismos de um domínio antes de confirmar o isomorfismo. Sem considerar todos os morfismos possíveis, pode parecer que dois objetos são isomórficos quando na verdade não são. Um precursor do isomorfismo é a cardinalidade dos domínios. Esse valor precisa ser o mesmo para ambos os domínios. Se os domínios tiverem cardinalidade incompatível, o homomorfismo entre eles não pode ser revertido pois de um domínio você terá mais de um mapeamento de elemento para o mesmo coelemento. Portanto, nós precisamos de um grupo de morfismos entre domínios para definir o isomorfismo. Normalmente nós precisamos de dois morfismos, uma das camisas para as calças e outro das calças para as camisas, que estabeleçam uma correspondência biunívoca entre os tamanhos das camisas e das calças. Esses morfismos devem ser inversos um do outro, ou seja, se um morfismo leva uma camisa de tamanho "pequeno" para uma calça de tamanho "28", o outro morfismo deve levar uma calça de tamanho "28" para uma camisa de tamanho "pequeno". ". E quando nós compomos esses dois morfismos, deve nos dar o morfismo de identidade para o domínio que iniciamos.
Essa exigência de axiomas na teoria das categorias inferiu a necessidade de morfismos de automapeamento. Há, no entanto, ainda um debate quanto à sua relevância na definição de uma categoria.
Seguindo em frente, vamos ilustrar um isomorfismo em MQL5. Eu reescrevi a maior parte do script compartilhado no artigo anterior para poder incluir os modelos. Todas as classes da classe de elemento até a classe de categoria incorporam o uso de tipos de dados do modelo para flexibilidade. No entanto, eu 'enumerei' os tipos disponíveis na classe de categoria. São eles: 'datetime', 'string', 'double' e int. O tipo 'int' é o padrão e será usado se um tipo de dados como 'color', por exemplo, estiver sendo usado. Todo o código está anexado no final do artigo. Aqui está a nossa nova classe de homomorfismo.
//+------------------------------------------------------------------+ //| HOMO-MORPHISM CLASS | //+------------------------------------------------------------------+ template <typename TD,typename TC> class CHomomorphism : public CObject { protected: int morphisms; public: CDomain<TD> domain; CDomain<TC> codomain; CMorphism<TD,TC> morphism[]; int Morphisms() { return(morphisms); } bool Morphisms(int Value) { if(Value>=0 && Value<INT_MAX) { morphisms=Value; ArrayResize(morphism,morphisms); return(true); } return(false); } bool Get(int MorphismIndex,CMorphism<TD,TC> &Morphism) { if(MorphismIndex>=0 && MorphismIndex<Morphisms()) { Morphism=morphism[MorphismIndex]; Morphism.domain=domain; Morphism.codomain=codomain; return(true); } return(false); } template <typename TDD,typename TDC> bool Set(int ValueIndex,CMorphism<TDD,TDC> &Value) { if ( (string(typename(TD))!=string(typename(TDD))) || (string(typename(TC))!=string(typename(TDC))) || ) { return(false); } // if(ValueIndex>=0 && ValueIndex<Morphisms()) { Value.domain=domain; Value.codomain=codomain; if(Index(Value)==-1) { morphism[ValueIndex]=Value; return(true); } } return(false); }; template <typename TDD,typename TDC> int Index(CMorphism<TDD,TDC> &Value) { int _index=-1; // if ( (string(typename(TD))!=string(typename(TDD))) || (string(typename(TC))!=string(typename(TDC))) || ) { return(_index); } // for(int m=0; m<morphisms; m++) { if(MorphismMatch(Value,morphism[m])) { _index=m; break; } } return(_index); } CHomomorphism(void){ Morphisms(0); }; ~CHomomorphism(void){}; };
Para testar o isomorfismo, nós usaremos os mesmos domínios do artigo anterior e os executaremos por meio da função 'IsIsomorphic'. Esta função retorna um valor booleano como true indicando sucesso e false indicando falha.
//+------------------------------------------------------------------+ //| Get Isomorphisms function | //+------------------------------------------------------------------+ template <typename TD,typename TC> bool IsIsomorphic(CDomain<TD> &A,CDomain<TC> &B,CHomomorphism<TD,TC> &Output[]) { if(A.Cardinality()!=B.Cardinality()) { return(false); } int _cardinal=A.Cardinality(); uint _factorial=MathFactorial(_cardinal); ArrayResize(Output,_factorial); for(uint f=0;f<_factorial;f++) { ArrayResize(Output[f].morphism,_cardinal); // for(int c=0;c<_cardinal;c++) { Output[f].morphism[c].domain=A; Output[f].morphism[c].codomain=B; } } int _index=0; CDomain<TC> _output[];ArrayResize(_output,_factorial); GetIsomorphisms(B, 0, _cardinal-1, _cardinal, _index, _output); for(uint f=0;f<_factorial;f++) { for(int c=0;c<_cardinal;c++) { CElement<TC> _ec; if(_output[f].Get(c,_ec)) { for(int cc=0;cc<_cardinal;cc++) { CElement<TC> _ecc; if(B.Get(cc,_ecc)) { if(ElementMatch(_ec,_ecc)) { if(Output[f].morphism[c].Codomain(cc)) { break; } } } } } if(Output[f].morphism[c].Domain(c)) { } } } return(true); }
O homomorfismo de saída, porém, precisa ser especificado no conjunto inicial e, em nosso caso, nós estamos usando a variável '_h_i'. Esse valor de saída, que é um array da classe de homomorfismo, incluirá uma enumeração de todos os possíveis homomorfismos isomórficos entre os dois domínios de entrada.
//IDENTITY CHomomorphism<int,int> _h_i[]; //is evens isomorphic to odds? if(IsIsomorphic(_evens,_odds,_h_i)) { printf(__FUNCSIG__+" evens can be isomorphic to odds by up to: "+IntegerToString(ArraySize(_h_i))+" homomorphisms. Estes podem ser... "); for(int s=0; s<ArraySize(_h_i); s++) { printf(__FUNCSIG__); string _print=""; for(int ss=0; ss<ArraySize(_h_i[s].morphism); ss++) { _print+=PrintMorphism(_h_i[s].morphism[ss],0); } printf(_print+" at: "+IntegerToString(s)); } }
Se executarmos este código, nós devemos ter os logs abaixo.
2023.01.26 10:42:56.909 ct_2 (EURGBP.ln,H1) void OnStart() evens can be isomorphic to odds by up to: 6 homomorphisms. Estes podem ser... 2023.01.26 10:42:56.909 ct_2 (EURGBP.ln,H1) void OnStart() 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (0)|----->(1) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (2)|----->(3) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (4)|----->(5) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) at: 0 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) void OnStart() 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (0)|----->(1) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (2)|----->(5) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (4)|----->(3) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) at: 1 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) void OnStart() 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (0)|----->(3) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (2)|----->(1) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (4)|----->(5) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) at: 2 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) void OnStart() 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (0)|----->(3) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (2)|----->(5) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (4)|----->(1) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) at: 3 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) void OnStart() 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (0)|----->(5) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (2)|----->(3) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (4)|----->(1) 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) at: 4 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) void OnStart() 2023.01.26 10:42:56.910 ct_2 (EURGBP.ln,H1) (0)|----->(5) 2023.01.26 10:42:56.911 ct_2 (EURGBP.ln,H1) (2)|----->(1) 2023.01.26 10:42:56.911 ct_2 (EURGBP.ln,H1) (4)|----->(3) 2023.01.26 10:42:56.911 ct_2 (EURGBP.ln,H1) at: 5
Isso é com um domínio de pares cujo a saída é:
2023.01.26 10:42:56.899 ct_2 (EURGBP.ln,H1) void OnStart() evens are... {(0),(2),(4)}
E um domínio de probabilidades cujo a saída é:
2023.01.26 10:42:56.899 ct_2 (EURGBP.ln,H1) void OnStart() odds are... {(1),(3),(5)}
Associação
Na teoria das categorias, o axioma da Associação é uma das propriedades básicas que uma categoria deve satisfazer. Usando um exemplo de uma categoria de vestuário em que os domínios são itens de vestuário específicos, como camisas, calças e sapatos, os morfismos seriam as funções que combinam as roupas dependendo da adequação. O axioma da associação, também conhecido como a "lei da associatividade", afirma que a composição dos morfismos é associativa. Isso significa que, ao compor vários morfismos, a ordem em que são aplicados não afeta o resultado final.
Por exemplo, considere o morfismo "é usado com" em todos os 3 domínios de roupas (camisas, calças e sapatos). Digamos que nós temos um morfismo f: camiseta -> camisa de botão, g: camisa de botão -> jeans e h: jeans -> tênis. Usando o axioma da associação, nós podemos definir a composição desses morfismos como h o (g o f) = (h o g) o f. Isso significa que a ordem dos morfismos não importa e podemos agrupá-los da maneira que quisermos. Isso torna a definição de uma categoria mais simples, pois nos permite evitar ter que calcular os parênteses de múltiplos morfismos. Em vez disso, nós podemos agrupar os morfismos, independentemente de sua ordem, e o resultado final será o mesmo.
Vamos ver isso em ação no MQL5. Nós precisamos recompor a classe de categoria que eu compartilhei no artigo anterior.
//+------------------------------------------------------------------+ //| CATEGORY CLASS | //+------------------------------------------------------------------+ class CCategory { protected: int domains_datetime; int domains_string; int domains_double; int domains_int; int ontologies; CDomain<datetime> domain_datetime[]; CDomain<string> domain_string[]; CDomain<double> domain_double[]; CDomain<int> domain_int[]; COntology ontology[]; public: int Domain(string T) { if(T=="datetime"){ return(domains_datetime); } else if(T=="string"){ return(domains_string); } else if(T=="double"){ return(domains_double); } return(domains_int); }; bool Domain(string T,int Value) { if(Value>=0 && Value<INT_MAX) { if(T=="datetime") { if(ArrayResize(domain_datetime,Value)>=Value) { domains_datetime=Value; return(true); } } else if(T=="string") { if(ArrayResize(domain_string,Value)>=Value) { domains_string=Value; return(true); } } else if(T=="double") { if(ArrayResize(domain_double,Value)>=Value) { domains_double=Value; return(true); } } else //if(T=="int") { if(ArrayResize(domain_int,Value)>=Value) { domains_int=Value; return(true); } } } return(false); }; int Ontology(){ return(ontologies); }; bool Ontology(int Value){ if(Value>=0 && Value<INT_MAX){ ontologies=Value; ArrayResize(ontology,ontologies); return(true); } return(false); }; template <typename T> bool Set(int ValueIndex,CDomain<T> &Value) { if(Index(Value)==-1 && ValueIndex>=0) { if ( ValueIndex<Domain(string(typename(T))) || (ValueIndex>=Domain(string(typename(T))) && Domain(string(typename(T)),ValueIndex+1)) ) { if(string(typename(T))=="datetime") { domain_datetime[ValueIndex]=Value; return(true); } else if(string(typename(T))=="string") { domain_string[ValueIndex]=Value; return(true); } else if(string(typename(T))=="double") { domain_double[ValueIndex]=Value; return(true); } else //if(string(typename(T))=="int") { domain_int[ValueIndex]=Value; return(true); } } } // return(false); }; template <typename T> bool Get(int DomainIndex,CDomain<T> &D) { if(DomainIndex>=0 && DomainIndex<Domain(string(typename(T)))) { if(string(typename(T))=="datetime") { D=domain_datetime[DomainIndex]; return(true); } else if(string(typename(T))=="string") { D=domain_string[DomainIndex]; return(true); } else if(string(typename(T))=="double") { D=domain_double[DomainIndex]; return(true); } else //if(string(typename(T))=="int") { D=domain_int[DomainIndex]; return(true); } } return(false); }; bool Set(int ValueIndex,COntology &Value) { if ( ValueIndex>=0 && ValueIndex<Ontology() ) { ontology[ValueIndex]=Value; return(true); } else if(ValueIndex>=Ontology()) { if(Ontology(Ontology()+1)) { ontology[Ontology()-1]=Value; return(true); } } // return(false); }; bool Get(int OntologyIndex,COntology &O) { if(OntologyIndex>=0 && OntologyIndex<Ontology()) { O=ontology[OntologyIndex]; return(true); } return(false); }; template <typename T> int Index(CDomain<T> &Value) { int _index=-1; // for(int d=0; d<Domain(string(typename(T))); d++) { if(string(typename(T))=="string") { if(DomainMatch(Value,domain_string[d])) { _index=d; break; } } else if(string(typename(T))=="datetime") { if(DomainMatch(Value,domain_int[d])) { _index=d; break; } } else if(string(typename(T))=="double") { if(DomainMatch(Value,domain_double[d])) { _index=d; break; } } else if(string(typename(T))=="int") { if(DomainMatch(Value,domain_int[d])) { _index=d; break; } } } return(_index); } int Index(COntology &Value) { int _index=-1; // for(int o=0; o<Ontology(); o++) { if(!OntologyMatch(Value,ontology[o])) { _index=o; break; } } return(_index); } CCategory() { domains_datetime=0; domains_string=0; domains_double=0; domains_int=0; ontologies=0; }; ~CCategory() { }; };
Observe os tipos de dados 'enumerados' que são permitidos. Eu tentarei tornar isso mais claro integrando-os como um objeto em uma única matriz em artigos futuros. A função 'FillDomain' também foi adicionada, além da do artigo anterior que preenchia um domínio com números naturais.
//+------------------------------------------------------------------+ //| Fill Domain(Set) with one-cardinal elements from input E array. | //+------------------------------------------------------------------+ template <typename TD,typename TE> void FillDomain(CDomain<TD> &D,CElement<TE> &E[]) { if(string(typename(TD))!=string(typename(TE))) { return; } int _cardinal=ArraySize(E); // if(_cardinal<0||INT_MAX<=_cardinal) { return; } //Set its cardinal to input array size if(D.Cardinality(_cardinal)) { for(int c=0;c<_cardinal;c++) { D.Set(c,E[c],true); } } }
Portanto, para verificar a associação, nós criaremos a categoria '_ca'. Em seguida, declaramos 3 conjuntos simples do tipo string e cada um deles é preenchido com um tipo de roupa. Copiamos esses conjuntos (arrays) em novos arrays de elementos ('_et', '_ep', '_es') e adicionamos cada um desses elementos ao seu próprio domínio ('_dt', '_dp', '_ds'). Feito isso, nós definimos o número de domínios para a nossa categoria como 3 e, em seguida, passamos a definir o domínio em cada índice com os domínios recém-criados que foram preenchidos com os elementos do tipo de roupa.
//ASSOCIATION CCategory _ca; string _tops[__EA]={"T-shirt","button-up","polo","sweatshirt","tank top"}; //domain 0 string _pants[__EA]={"jeans","slacks","khakis","sweatpants","shorts"}; //domain 1 string _shoes[__EA]={"sneakers","dress shoes","loafers","running shoes","sandals"}; //domain 2 CElement<string> _et[];ArrayResize(_et,__EA); CElement<string> _ep[];ArrayResize(_ep,__EA); CElement<string> _es[];ArrayResize(_es,__EA); for(int e=0;e<__EA;e++) { _et[e].Cardinality(1); _et[e].Set(0,_tops[e]); _ep[e].Cardinality(1); _ep[e].Set(0,_pants[e]); _es[e].Cardinality(1); _es[e].Set(0,_shoes[e]); } CDomain<string> _dt,_dp,_ds; FillDomain(_dt,_et);FillDomain(_dp,_ep);FillDomain(_ds,_es); // if(_ca.Domain("string",__DA))//resize domains array to 3 { if(_ca.Set(0,_dt) && _ca.Set(1,_dp) && _ca.Set(2,_ds))//assign each filled domain above to a spot (index) within the category { if(_ca.Domain("string")==__DA)//check domains count { for(int e=0;e<__EA;e++) { COntology _o_01_2; CMorphism<string,string> _m1_01_2,_m2_01_2; SetCategory(_ca,0,1,e,e,_o_01_2," is worn with ",_m1_01_2); SetCategory(_ca,1,2,e,e,_o_01_2," is worn with ",_m2_01_2,ONTOLOGY_POST);printf(__FUNCSIG__+" (0 & 1) followed by 2 Log is: "+_o_01_2.ontology); COntology _o_0_12; CMorphism<string,string> _m1_0_12,_m2_0_12; SetCategory(_ca,1,2,e,e,_o_0_12," is worn with ",_m1_0_12); SetCategory(_ca,0,2,e,e,_o_0_12," is worn with ",_m2_0_12,ONTOLOGY_PRE);printf(__FUNCSIG__+" 0 following (1 & 2) Log is: "+_o_0_12.ontology); } } } }
Para verificar a associatividade, nós exibiremos os resultados dos morfismos nos logs da ontologia. Para isso nós vamos criar uma classe 'COntology'. Isso é descrito abaixo como uma enumeração e uma estrutura com o mesmo nome.
//+------------------------------------------------------------------+ //| ONTOLOGY ENUM | //+------------------------------------------------------------------+ enum EOntology { ONTOLOGY_PRE=-1, ONTOLOGY_NEW=0, ONTOLOGY_POST=1 }; //+------------------------------------------------------------------+ //| ONTOLOGY STRUCT | //+------------------------------------------------------------------+ struct SOntology { int in; int out; SOntology() { in=-1; out=-1; }; ~SOntology(){}; }; //+------------------------------------------------------------------+ //| ONTOLOGY CLASS | //+------------------------------------------------------------------+ class COntology { protected: int facts; SOntology types[]; SOntology universe[]; public: string ontology; int Facts() { return(facts); } bool Facts(int Value) { if(Value>=0 && Value<INT_MAX) { facts=Value; ArrayResize(types,facts); ArrayResize(universe,facts); return(true); } return(false); } bool GetType(int TypeIndex,int &TypeIn,int &TypeOut) { if(TypeIndex>=0 && TypeIndex<Facts()) { TypeIn=types[TypeIndex].in; TypeOut=types[TypeIndex].out; return(true); } return(false); } bool SetType(int ValueIndex,int ValueIn,int ValueOut) { if(ValueIndex>=0 && ValueIndex<Facts()) { types[ValueIndex].in=ValueIn; types[ValueIndex].out=ValueOut; return(true); } else if(ValueIndex>=0 && ValueIndex>=Facts() && ValueIndex<INT_MAX-1) { if(Facts(ValueIndex+1)) { types[ValueIndex].in=ValueIn; types[ValueIndex].out=ValueOut; return(true); } } return(false); } bool GetUniverse(int UniverseIndex,int &UniverseIn,int &UniverseOut) { if(UniverseIndex>=0 && UniverseIndex<Facts()) { UniverseIn=universe[UniverseIndex].in; UniverseOut=universe[UniverseIndex].out; return(true); } return(false); } bool SetUniverse(int ValueIndex,int ValueIn,int ValueOut) { if(ValueIndex>=0 && ValueIndex<Facts()) { universe[ValueIndex].in=ValueIn; universe[ValueIndex].out=ValueOut; return(true); } else if(ValueIndex>=0 && ValueIndex>=Facts() && ValueIndex<INT_MAX-1) { if(Facts(ValueIndex+1)) { universe[ValueIndex].in=ValueIn; universe[ValueIndex].out=ValueOut; return(true); } } return(false); } string old_hash; string new_hash; COntology() { ontology=""; facts=0; ArrayResize(types,facts); ArrayResize(universe,facts); old_hash=""; new_hash=""; }; ~COntology(){}; };
A partir da saída da ontologia, a execução do script deve nos fornecer os logs abaixo.
2023.01.26 10:42:56.911 ct_2 (EURGBP.ln,H1) void OnStart() (0 & 1) followed by 2 Log is: T-shirt is worn with jeans is worn with sneakers 2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1) void OnStart() 0 following (1 & 2) Log is: T-shirt is worn with jeans is worn with sneakers 2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1) void OnStart() (0 & 1) followed by 2 Log is: button-up is worn with slacks is worn with dress shoes 2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1) void OnStart() 0 following (1 & 2) Log is: button-up is worn with slacks is worn with dress shoes 2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1) void OnStart() (0 & 1) followed by 2 Log is: polo is worn with khakis is worn with loafers 2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1) void OnStart() 0 following (1 & 2) Log is: polo is worn with khakis is worn with loafers 2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1) void OnStart() (0 & 1) followed by 2 Log is: sweatshirt is worn with sweatpants is worn with running shoes 2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1) void OnStart() 0 following (1 & 2) Log is: sweatshirt is worn with sweatpants is worn with running shoes 2023.01.26 10:42:56.912 ct_2 (EURGBP.ln,H1) void OnStart() (0 & 1) followed by 2 Log is: tank top is worn with shorts is worn with sandals 2023.01.26 10:42:56.913 ct_2 (EURGBP.ln,H1) void OnStart() 0 following (1 & 2) Log is: tank top is worn with shorts is worn with sandals
Em resumo, o axioma da associação facilita a definição de uma categoria ao permitir que a composição de morfismos seja associativa, o que elimina a necessidade de calcular os parênteses ao definir os múltiplos morfismos. Isso torna mais simples entender as relações entre os objetos em uma categoria, neste caso, os itens de vestuário em todos os três domínios; camisas, calças e sapatos.
Diagramas Comutativos
Um diagrama comutativo é um diagrama que representa a relação entre os dois morfismos em uma categoria. Ele consiste em um conjunto de domínios, morfismos e suas composições, organizados de maneira específica para mostrar que os morfismos comutam, o que significa que a ordem em que são compostos não importa. Isso implica que, para quaisquer três domínios A, B, e C em uma categoria, e para seus morfismos f: A -> B, g: B -> C, e h: A -> C; a composição desses morfismos deve satisfazer:
f o g = h
Um exemplo de comutação usando preços de câmbio pode ser a arbitragem; a relação entre o preço de, digamos, EURUSD, EURJPY e USDJPY. Neste exemplo, os domínios podem ser as próprias moedas (EUR, USD, JPY), enquanto os morfismos podem representar o processo de conversão de uma moeda em outra com base na taxa de câmbio. Por exemplo, seja f: EUR -> USD o morfismo que representa o processo de conversão de EUR para USD à taxa de câmbio EURUSD; seja g: USD -> JPY o morfismo que representa o processo de conversão de USD para JPY à taxa de câmbio de USDJPY; e seja h: EUR -> JPY o morfismo que representa a conversão de EUR para JPY. Seguindo a regra de comutação acima: fog = h, isso se traduziria em:
conversão do EUR para USD à taxa EURUSD e, em seguida, conversão do USD para JPY à taxa USDJPY = conversão do EUR para JPY à taxa EURJPY.
Vamos ilustrar isso com MQL5. Vamos declarar uma categoria '_cc' e preenchê-la com 3 domínios, cada um com 2 moedas. Os domínios podem ser considerados como portfólios na alocação de ativos. Como no axioma de associação, nós preencheremos e verificaremos os nossos valores de categoria usando os logs de ontologia conforme abaixo.
//COMMUTATION CCategory _cc; string _a[__EC]={"EUR","GBP"}; //domain 0 string _b[__EC]={"USD","CAD"}; //domain 1 string _c[__EC]={"CHF","JPY"}; //domain 2 CElement<string> _e_a[];ArrayResize(_e_a,__EC); CElement<string> _e_b[];ArrayResize(_e_b,__EC); CElement<string> _e_c[];ArrayResize(_e_c,__EC); for(int e=0;e<__EC;e++) { _e_a[e].Cardinality(1); _e_a[e].Set(0,_a[e]); _e_b[e].Cardinality(1); _e_b[e].Set(0,_b[e]); _e_c[e].Cardinality(1); _e_c[e].Set(0,_c[e]); } CDomain<string> _d_a,_d_b,_d_c; FillDomain(_d_a,_e_a);FillDomain(_d_b,_e_b);FillDomain(_d_c,_e_c); // if(_cc.Domain("string",__DC))//resize domains array to 3 { if(_cc.Set(0,_d_a) && _cc.Set(1,_d_b) && _cc.Set(2,_d_c))//assign each filled domain above to a spot (index) within the category { if(_cc.Domain("string")==__DC)//check domains count { for(int e=0;e<__EC;e++) { COntology _o_ab_bc; string _ab=_a[e]+_b[e],_bc=_b[e]+_c[e]; double _ab_bid=SymbolInfoDouble(_ab,SYMBOL_BID),_bc_bid=SymbolInfoDouble(_bc,SYMBOL_BID); string _aspect_ab=" is exchanged at: "+DoubleToString(_ab_bid,(int)SymbolInfoInteger(_ab,SYMBOL_DIGITS))+", for: "; string _aspect_bc=" is exchanged at: "+DoubleToString(_bc_bid,(int)SymbolInfoInteger(_bc,SYMBOL_DIGITS))+", for: "; CMorphism<string,string> _m_ab,_m_bc; SetCategory(_cc,0,1,e,e,_o_ab_bc,_aspect_ab,_m_ab); SetCategory(_cc,1,2,e,e,_o_ab_bc,_aspect_bc,_m_bc,ONTOLOGY_POST);printf(__FUNCSIG__+" a to b then b to c logs: "+_o_ab_bc.ontology); COntology _o_ac; string _ac=_a[e]+_c[e]; string _aspect_ac=" is exchanged at: "+DoubleToString(SymbolInfoDouble(_ac,SYMBOL_BID),(int)SymbolInfoInteger(_ac,SYMBOL_DIGITS))+", for: "; CMorphism<string,string> _m_ac; SetCategory(_cc,0,2,e,e,_o_ac,_aspect_ac,_m_ac);printf(__FUNCSIG__+" a to c logs: "+_o_ac.ontology+" vs product of bid rate for ab and bc of: "+DoubleToString(_ab_bid*_bc_bid,(int)SymbolInfoInteger(_ac,SYMBOL_DIGITS)));//ontology } } } }
Verificamos a comutação comparando a taxa do morfismo de comutação '_m_ac' com o produto das duas taxas obtidas dos morfismos '_m_ab' e '_m_bc'. Existem discrepâncias, mas elas se devem principalmente à qualidade dos dados históricos da corretora e o spread da conta (somente os bids são usados). A execução desse script deve nos fornecer esses logs.
2023.01.26 17:27:19.093 ct_2 (EURGBP.ln,H1) void OnStart() a to b then b to c logs: EUR is exchanged at: 1.08966, for: USD is exchanged at: 0.91723, for: CHF 2023.01.26 17:27:19.093 ct_2 (EURGBP.ln,H1) void OnStart() a to c logs: EUR is exchanged at: 0.99945, for: CHF vs product of bid rate for ab and bc of: 0.99947 2023.01.26 17:27:19.093 ct_2 (EURGBP.ln,H1) void OnStart() a to b then b to c logs: GBP is exchanged at: 1.65097, for: CAD is exchanged at: 97.663, for: JPY 2023.01.26 17:27:19.093 ct_2 (EURGBP.ln,H1) void OnStart() a to c logs: GBP is exchanged at: 161.250, for: JPY vs product of bid rate for ab and bc of: 161.239
Logs da Ontologia
Ontologias são resumos subjetivos de uma categoria. Eles servem como uma ferramenta importante na teoria das categorias porque fornecem uma maneira de interpretar a estrutura e as relações dos domínios via morfismos em uma determinada categoria. Em outras palavras, eles são uma estrutura matemática (ou modelo de dados, equivalente a um esquema de banco de dados) que descreve os tipos de domínios e seus morfismos no domínio. Existem vários tipos de ontologias, entre elas: - Ontologias taxonômicas descrevem um conjunto de objetos e suas subclasses e definem os relacionamentos entre eles em termos de relacionamentos "é-um".
- Ontologias hierárquicas descrevem um conjunto de objetos e suas propriedades e definem os relacionamentos entre eles em termos de relacionamentos "parte de".
- Ontologias relacionais descrevem um conjunto de objetos e seus relacionamentos, e definem os relacionamentos entre eles em termos de relacionamentos binários arbitrários.
Para um sistema de negociação forex, uma ontologia relacional pode ser mais apropriada. Isso permitiria a modelagem de vários tipos de estratégias de negociação e as relações entre elas, já que as estratégias são mais eficazes em determinadas condições de mercado. Além disso, as ontologias relacionais podem ser facilmente estendidas para incluir informações adicionais, como os dados históricos, que podem ser úteis no desenvolvimento de um sistema de negociação.
As ontologias relacionais entram em ação quando usadas em vários domínios na teoria da categoria que podem ser demonstradas usando vários exemplos nos mercados financeiros. Aqui estão cinco exemplos:
- Pares de Moedas: O mercado forex é composto por pares de moedas, que são os conjuntos de duas moedas que são negociadas uma contra a outra. A relação entre essas moedas pode ser modelada usando uma ontologia relacional, onde os pares de moedas são considerados como domínios e a taxa de câmbio é considerada como o morfismo que as conecta. Um exemplo disso já foi compartilhado acima com o diagrama comutativo.
- Os dados das séries temporais: os preços do Forex são frequentemente representados como dados de séries temporais, que podem ser modelados usando uma ontologia relacional onde os dados das séries temporais são considerados como um domínio e as mudanças de preços ao longo do tempo são consideradas como morfismos.
- Indicadores Técnicos: Indicadores técnicos, como médias móveis ou índices de força relativa, podem ser usados para analisar os preços de forex. Esses indicadores podem ser modelados usando uma ontologia relacional onde o indicador é considerado como um domínio e os valores do indicador são considerados como morfismos.
- Estratégias de negociação: os traders geralmente usam várias estratégias de negociação, como estratégias de acompanhamento de tendências ou baseadas em impulso. Essas estratégias podem ser modeladas usando uma ontologia relacional onde a estratégia de negociação é considerada como um domínio e as negociações que são executadas, com base na estratégia, são consideradas como morfismos.
- Livro de Ofertas: O livro de ofertas é um registro de todas as ordens de compra e venda que foram colocadas no mercado cambial. Isso pode ser modelado (se fornecido por uma corretora) usando uma ontologia relacional onde o livro de ofertas é considerado um domínio e as ordens colocadas são consideradas como morfismos.
No geral, as ontologias relacionais são úteis na teoria da categoria quando usadas em vários domínios na negociação porque permitem a modelagem e análise de sistemas e relacionamentos complexos de maneira clara e estruturada. As ontologias empregam 'tipos' e 'aspectos' para apresentar uma visão subjetiva de uma categoria. Um tipo pode ser pensado como um grupo de domínios dentro de uma categoria particular. Pode ser simples ou composto. Quando simples, ele contém apenas um domínio. Quando composto, ele reúne mais de um domínio. Os aspectos estão para os tipos assim como os morfismos estão para os domínios dentro de uma categoria. Uma ontologia relacional baseada em pares de moedas no mercado de câmbio (forex) pode ser modelada da seguinte forma:
Tipos:
- Par de Moedas: O par de moedas é o tipo principal nesta ontologia, representando as duas moedas que estão sendo negociadas uma contra a outra. Por exemplo, o par de moedas "EUR/USD" representa a taxa de câmbio entre o Euro e o Dólar Americano.
- Taxa de câmbio: A taxa de câmbio é a taxa na qual uma moeda pode ser trocada por outra. Ela representa o morfismo entre os objetos do par de moedas. Por exemplo, a taxa de câmbio para o par de moedas EUR/USD pode ser de 1.20, o que significa que 1 euro pode ser trocado por 1.20 dólares americanos.
- Time: Time é um tipo que pode ser usado para representar o horário em que a taxa de câmbio se aplica. Ele pode ser usado para conectar o morfismo da taxa de câmbio com os dados das séries temporais.
Aspectos:
- Histórico das taxas de câmbio: O histórico das taxas de câmbio são as taxas de câmbio registradas em diferentes pontos no tempo. Eles podem ser usados para analisar tendências e padrões no mercado de câmbio.
- Volatilidade: A volatilidade é uma medida de quanto a taxa de câmbio muda ao longo do tempo. Ela pode ser usada para avaliar o risco associado a um determinado par de moedas.
- Correlação: A correlação é uma medida da relação entre dois pares de moedas. Ela pode ser usada para identificar as oportunidades de diversificação ou hedge no mercado cambial.
No geral, esta ontologia relacional permite uma representação clara e estruturada das relações entre os pares de moedas, taxas de câmbio, tempo e outros aspectos do mercado de câmbio. Ele pode ser usado para analisar a dinâmica do mercado para a tomada de decisões informadas. Os universos de Grothendieck são usados para definir o conceito de um universo de tipos, que é fundamental dentro das ontologias da teoria das categorias, um universo de tipos é um conjunto de tipos dentro de uma determinada categoria. Ele permite a classificação dos tipos e aborda o problema dos "conjuntos de conjuntos".
Para ver as ontologias em ação, vejamos um exemplo na indústria financeira. Diferentes entidades, como a Securities and Exchange Commission (SEC) e um fundo de hedge, podem usar ontologias para organizar e categorizar dados financeiros, na mesma categoria, de maneiras diferentes. Isso pode levar a diferentes tipos e aspectos dos dados representados nas ontologias utilizadas por cada entidade. Do ponto de vista da SEC, uma ontologia pode ser utilizada para organizar os dados relacionados a valores mobiliários e atividades de negociação, com foco em compliance e questões regulatórias. Isso pode incluir tipos como "títulos", "atividade de negociação", "negociação com informações privilegiadas" e "violações das leis de valores mobiliários". A ontologia também pode incluir aspectos relacionados à conformidade e execução, como "investigações" e "penalidades". Do ponto de vista de um fundo hedge, uma ontologia, da mesma categoria, pode ser utilizada para organizar os dados relacionados a estratégias de investimento, gestão de portfólio e métricas de desempenho. Isso pode incluir tipos como "estratégias de investimento", "gerenciamento de portfólio", "métricas de desempenho" e "gerenciamento de riscos". A ontologia também pode incluir aspectos relacionados à operação e gestão do fundo, como “ativos sob gestão” e “administradores de fundos”. Como podemos ver, embora ambas as entidades possam estar usando ontologias para organizar dados financeiros, os tipos e aspectos representados em suas ontologias são diferentes, refletindo os diferentes objetivos, perspectivas e preocupações da SEC versus um fundo de hedge. Assim, a ontologia da SEC estaria focada em compliance, regulações e violações na negociação de valores mobiliários, enquanto a ontologia dos fundos hedge estaria focada em investimentos, gestão de riscos e gestão de carteiras.
Passando a ilustrar os tipos ainda mais em forex, os tipos simples e compostos referem-se aos tipos de dados que podem ser usados para representar diferentes aspectos do mercado. Tipos simples são tipos de dados básicos que podem ser representados por um único valor. Por exemplo, em forex, a taxa de câmbio entre duas moedas pode ser considerada um tipo simples, representado por um único valor como 1.20 (o que significa que 1 unidade da moeda base pode ser trocada por 1.20 unidades da moeda de cotação). Os tipos compostos, por outro lado, são os tipos de dados compostos de vários valores ou outros tipos de dados. Por exemplo, um gráfico de velas pode ser considerado um tipo composto, pois ele é composto por vários valores, como preço de abertura, preço de fechamento, máxima e mínima do preço para um determinado período de tempo. Em termos de aspectos, aspectos simples são aqueles que conectam dois tipos simples, por exemplo, a taxa de câmbio entre duas moedas pode ser considerada um aspecto simples. Aspectos compostos são aqueles que conectam dois tipos compostos ou um tipo composto e um tipo simples, por exemplo, uma estratégia de negociação pode ser considerada um aspecto composto, pois ele conecta a estratégia com os negócios que são executados com base nela. No geral, tipos e aspectos simples são blocos de construção básicos que podem ser usados para representar informações básicas em ontologias, enquanto tipos e aspectos compostos são tipos de dados mais complexos compostos de vários valores ou outros tipos de dados, que podem ser usados para representar aspectos mais complexos do sistema que está sendo modelado.
Os logs de ontologia são uma forma de organizar e representar o conhecimento, fornecendo uma estrutura lógica para o domínio de interesse. Eles ajudam a definir os conceitos, propriedades e relacionamentos dentro de um domínio, subdomínio, tarefa, instância ou processo específico. Um log de ontologia é uma representação formal de um conjunto de conceitos, propriedades e relacionamentos que existem dentro de um domínio específico. Ele é usado para definir a estrutura do conhecimento dentro desse domínio e para fornecer uma representação consistente e lógica do conhecimento. Isso torna mais fácil para as máquinas e humanos entender e usar as informações dentro do domínio. Logs de ontologia podem ser usados em vários campos, como inteligência artificial, processamento de linguagem natural, representação de conhecimento e ciência da informação. Eles são comumente usados em conjunto com outros tipos de ontologias, como ontologias superiores e ontologias de domínio, para fornecer uma visão abrangente de um domínio. Logs de ontologia são normalmente representados em um formato legível por máquina, como OWL (Web Ontology Language) ou RDF (Resource Description Framework), o que permite que sejam facilmente processados e usados por máquinas. Eles também são legíveis por humanos, o que torna mais fácil para as pessoas entenderem e usarem as informações representadas no log da ontologia.
No contexto da teoria das categorias, os logs de ontologia são usados para organizar e representar o conhecimento, fornecendo uma estrutura lógica para o domínio de interesse. Eles ajudam a definir os conceitos, propriedades e relacionamentos dentro de um domínio, subdomínio, tarefa, instância ou processo específico. A teoria das categorias é um ramo da matemática que lida com a estrutura de sistemas matemáticos e fornece uma estrutura para modelar as relações entre objetos e morfismos. Os logs de ontologia, quando usados no contexto da teoria das categorias, fornecem uma maneira de organizar e representar o conhecimento dentro de um domínio de forma estruturada e lógica.
Existem vários tipos de logs de ontologia que são comumente usados na teoria das categorias, como:
- Ontologia superior: Uma ontologia superior é uma ontologia geral que fornece uma visão de alto nível de um domínio e define os conceitos e relacionamentos mais gerais que se aplicam a vários subdomínios. É uma maneira comum de fornecer uma estrutura unificadora em diferentes ontologias.
- Ontologia de domínio: Uma ontologia de domínio é uma ontologia específica que se concentra em um subdomínio particular dentro de um domínio maior. Ela define os conceitos e relacionamentos específicos desse subdomínio.
- Ontologia de tarefa: Uma ontologia de tarefa é uma ontologia específica que se concentra em uma tarefa ou problema particular dentro de um domínio. Ela define os conceitos e relacionamentos específicos para aquela tarefa ou problema.
- Ontologia de instância: Uma ontologia de instância é uma ontologia específica que se concentra nas instâncias de um conceito ou classe particular. Ela define as propriedades e relacionamentos específicos para essas instâncias.
- Ontologia de processo: Uma ontologia de processo é uma ontologia específica que se concentra nos processos ou ações que ocorrem dentro de um domínio. Ela define os conceitos e relacionamentos específicos para esses processos ou ações.
Esses tipos de logs de ontologia são usados para estruturar o conhecimento e os relacionamentos de um domínio e para facilitar a compreensão, representação e manipulação da informação. Eles ajudam a fornecer uma representação consistente e lógica do conhecimento dentro de um domínio e podem ser usados em conjunto com ontologias relacionais para fornecer uma visão abrangente de um domínio.
Um log de ontologia de processo é um tipo específico de log de ontologia que se concentra nos processos ou ações que ocorrem dentro de um domínio. Ela define os conceitos e relacionamentos específicos para esses processos ou ações. Assim, os tipos de aspectos que podem ser usados em um log de ontologia de processo dependerão do domínio específico e dos processos ou ações que estão sendo modelados. Aqui estão alguns exemplos de aspectos que podem ser usados em um log de ontologia de processo:
- Entradas e saídas: os aspectos de entrada e saída de um processo podem ser usados para definir os recursos, materiais ou informações necessárias para iniciar o processo e os produtos, serviços ou informações finais geradas pelo processo.
- Etapas ou Fases: O processo pode ser dividido em etapas ou fases menores e cada etapa pode ser definida como um conceito, representando as ações e objetivos daquela etapa. As relações entre as etapas também podem ser modeladas.
- Atores: Os atores são as entidades ou agentes envolvidos no processo, como pessoas, máquinas ou organizações. As relações entre os atores e seus papéis no processo podem ser definidas.
- Restrições: As restrições são as regras, regulamentos ou limitações que o processo deve cumprir. Este aspecto pode ser usado para definir as condições e requisitos que devem ser atendidos para que o processo seja concluído com sucesso.
- Métricas: Métricas são as medidas ou indicadores usados para avaliar o desempenho do processo, como eficiência, qualidade ou custo. Este aspecto pode ser usado para definir as medidas e indicadores usados para avaliar o processo e como eles são calculados.
- Aspectos temporais: Os aspectos temporais referem-se ao tempo do processo, como horário de início e término, duração e frequência do processo. Este aspecto pode ser usado para modelar os aspectos temporais do processo.
No geral, um log de ontologia de processo pode ser usado para modelar os vários aspectos de um processo, incluindo entradas e saídas, etapas ou fases, atores, restrições, métricas e aspectos temporais, e os relacionamentos entre eles, de maneira estruturada e lógica, o que pode facilitar a compreensão, representação e manipulação da informação. Um exemplo de uma ontologia de processo na categoria de mercado de câmbio (forex) poderia ser o processo de execução de uma negociação. A ontologia de processo definiria os conceitos e relacionamentos específicos para o processo de execução de uma negociação. Aqui está um exemplo de como os aspectos desta ontologia de processo podem ser modelados:
- Entradas e saídas: As entradas do processo incluem a estratégia de negociação, o par de moedas a ser negociado e o saldo da conta de negociação. A saída do processo é a negociação executada.
- Etapas ou Fases: O processo pode ser dividido em etapas ou fases menores, como selecionar o par de moedas, definir os parâmetros da negociação, fazer o envio da ordem e monitorar a negociação.
- Atores: Os atores envolvidos no processo incluem o trader, a plataforma de negociação e o mercado. O trader é o principal ator que inicia o processo, a plataforma de negociação é a ferramenta utilizada para executar a negociação e o mercado é o ambiente onde a negociação ocorre.
- Restrições: As restrições incluem regulamentações sobre margem, alavancagem e gerenciamento de risco. Essas restrições devem ser respeitadas para que a negociação seja concluída com sucesso.
- Métricas: As métricas usadas para avaliar o desempenho do processo incluem o lucro ou prejuízo na negociação, a relação risco-recompensa e a porcentagem de negociações bem-sucedidas.
- Aspectos temporais: Os aspectos temporais referem-se ao timing do processo, como o horário de início e término da negociação, a duração da negociação e a frequência das negociações.
Este log de ontologia de processo pode ser usado para modelar os vários aspectos do processo de execução de uma negociação no mercado de câmbio de forma estruturada e lógica. Ele pode ser utilizado para facilitar a compreensão, representação e manipulação das informações relacionadas ao processo de execução de uma negociação, e pode ser utilizado em conjunto com outros tipos de ontologias para fornecer uma visão abrangente dos mercados financeiros.
Conclusão
Em conclusão, a teoria das categorias fornece uma estrutura poderosa para modelar e analisar sistemas complexos, como os mercados financeiros. A implementação da teoria da categoria em MQL5 pode ajudar os traders a entender e navegar melhor no mercado, fornecendo uma representação lógica e estruturada das relações entre domínios e morfismos. O artigo destacou a importância das definições de axiomas de uma categoria na teoria das categorias e como elas fornecem uma base para modelar as relações entre domínios e morfismos. O artigo também discutiu o conceito de logs de ontologia e como eles podem ser usados para fornecer uma estrutura lógica a um assunto de interesse, neste caso os mercados financeiros. No geral, a implementação da teoria da categoria no MQL5 pode ser uma ferramenta valiosa para os traders que buscam obter uma compreensão mais profunda do mercado e tomar decisões de negociação mais informadas. Ele fornece uma abordagem estruturada e lógica para analisar o mercado, o que pode ajudar os traders a identificar padrões e oportunidades que, de outra forma, seriam difíceis de detectar.
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/11958
 Como desenvolver um sistema de negociação baseado no indicador Gator Oscillator
Como desenvolver um sistema de negociação baseado no indicador Gator Oscillator
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso