증분이 랜덤이면 가격은 랜덤 워크이고 정규 분포를 가지며 돈을 벌 수 없다는 것이 보장됩니다. 그러나 증분의 성격을 규정할 필요가 있습니다. 간단히 말해서 "무작위"라고 할 수 있습니다. 인생의 모든 것은 우연입니다. 버스에는 일정이 있지만 도착 시간은 무작위입니다. 임의의 가격 증분은 달의 위상과 상관 관계가 있을 수 있습니다. 예를 들어, 이로 인해 무작위가 아닌 것은 아닙니다. 랜덤 워크 증분을 얻으려면 독립적이고 균등하게 분산되어야 합니다.
문제의 사실은 가격 증가가 정규 분포를 따르지 않는다는 것입니다. 그렇지 않으면 돈이 보장됩니다.
문제는 가격 증가분이 정규 분포를 따르지 않는다는 것입니다. 그렇지 않으면 돈이 보장됩니다.
가격 증분은 정규 분포로 간주될 수 있습니다. 이는 현실에 충분히 가깝지만 iid 이면 작동하지 않습니다. 가격 증분은 자유도가 4 또는 5인 t-분포로 간주할 수 있습니다. 이는 일반 증분의 가정보다 현실에 훨씬 가깝습니다. 결과 프로세스는 랜덤 워크가 됩니다. 여기서는 일반적으로 증분 분포에 관계없이 정규 분포가 보장되지만 정규성은 아무 소용이 없습니다. 랜덤 워크로 돈을 벌 수 없습니다. 가격 인상은 고정된 것으로 간주될 수 있지만 거래될 수는 없습니다. 가격을 거래할 수 있지만 랜덤 워크이며 프로세스가 고정적이지 않습니다. 적어도 이 주제의 맥락에서.
가격 증분은 정규 분포로 간주될 수 있습니다. 이것은 현실에 충분히 가깝지만 iid 이면 작동하지 않습니다. 가격 증분은 자유도가 4 또는 5인 t-분포로 간주할 수 있습니다. 이는 일반 증분의 가정보다 현실에 훨씬 가깝습니다. 결과 프로세스는 랜덤 워크가 됩니다. 여기서는 일반적으로 증분 분포에 관계없이 정규 분포가 보장되지만 정규성은 아무 소용이 없습니다. 랜덤 워크로 돈을 벌 수 없습니다. 가격 인상은 고정된 것으로 간주될 수 있지만 거래될 수는 없습니다. 가격을 거래할 수 있지만 랜덤 워크이며 프로세스가 고정적이지 않습니다. 적어도 이 주제의 맥락에서.
토론을 계속 진행하기 위해 약간의 논쟁을 해도 될까요? 제가 지금 무슨 말을 하고 싶은지 잘 모르겠습니다. 특히 너무 늦었기 때문에. 하지만 여전히... 어떤 값의 증분이 정규 분포를 따른다면, 이것은 이 값이 제한된다는 것을 의미합니다. (잘못된?)
이전 진술에서 내가 틀리지 않았다면 수량 값 세트에는 최대값과 최소값이 있습니다. 또한 값의 값이 최대값 또는 최소값에 가까울수록 평균을 향해 변화할 가능성이 높아집니다. 사용할 수 있는 법입니다.
추신 내가 공격하고 있다고 생각하지 마십시오. 나는 똑똑한 사람과 이야기하고 싶을 뿐입니다.
토론을 계속 진행하기 위해 약간의 논쟁을 해도 될까요? 제가 지금 무슨 말을 하고 싶은지 잘 모르겠습니다. 특히 너무 늦었기 때문에. 그러나 여전히 ... 일부 값의 증분이 정규 분포라면 이 값이 제한됨을 의미합니다. (잘못된?)
이전 진술에서 내가 틀리지 않았다면 수량 값 세트에는 최대값과 최소값이 있습니다. 또한 값의 값이 최대값 또는 최소값에 가까울수록 평균을 향해 변경될 가능성이 높아집니다. 사용할 수 있는 법입니다.
추신 내가 공격하고 있다고 생각하지 마십시오. 나는 똑똑한 사람과 이야기하고 싶을 뿐입니다.
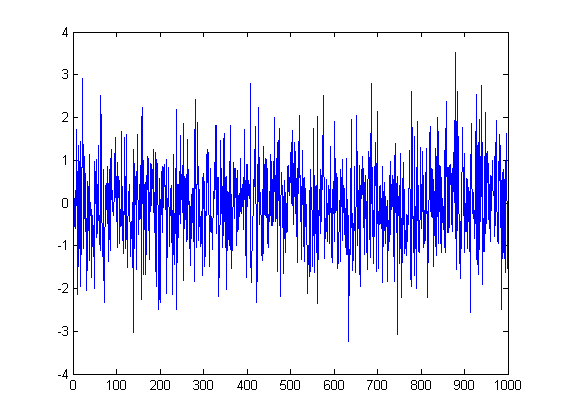
당신은 확실히 틀렸다. 분포의 특성은 크기를 제한하는 것에 대해 아무 말도 하지 않습니다. 물론 몇 가지 예외가 있지만 일반적으로 그렇습니다. 분포 매개변수에 의해 제한이 부과됩니다. 예: 정규 분포 변환 ~N(0,1). 이것은 고정된 과정이며 크기 제한이 있으며 거의 4 또는 -4에 도달하지 않습니다.
그리고 여기에 이러한 증분에서 나온 가격이 있습니다. 랜덤 산책입니다. 또한 정규 분포 ~N(0,sigma^2)를 갖지만 분산 매개변수는 일정하지 않지만 시간이 지남에 따라 증가합니다. 증분 수. 당연히 이 프로세스는 크기 제한이 없으며 동일한 확률로 모든 포인트를 방문합니다. 이것이 플레이어를 망치는 문제의 기초입니다. 만약 당신이 충분히 오랫동안(50:50) 절대적으로 공정한 게임을 한다면, 당신은 여전히 지게 될 것입니다. 왜냐하면. 조만간 이 곡선은 당신이 가진 돈보다 더 낮아질 것입니다.
그러나 1000번의 무작위 보행에서는 정규분포의 종 모양이 명확하게 보입니다.
그러나 평균으로 되돌리는 것에 대해 말하는 것은 완전히 다른 이야기입니다. 이것은 평균으로 되돌리는 과정입니다 - autoregressive(AR) x(i) = a * x(i-1) + e(i). e(i) 변환 ~N(0,1), a < 1.
거래된 평균 회귀 프로세스를 발견했다면 양배추가 든 바구니를 끌 시간이 있습니다. 당연히 매개변수(평균으로의 회귀율(a))에 따라 다르지만 어쨌든 모든 것이 좋습니다.
증분이 랜덤이면 가격은 랜덤 워크이고 정규 분포를 가지며 돈을 벌 수 없다는 것이 보장됩니다.
그러나 증분의 성격을 규정할 필요가 있습니다. 간단히 말해서 "무작위"라고 할 수 있습니다. 인생의 모든 것은 우연입니다. 버스에는 일정이 있지만 도착 시간은 무작위입니다. 임의의 가격 증분은 달의 위상과 상관 관계가 있을 수 있습니다. 예를 들어, 이로 인해 무작위가 아닌 것은 아닙니다.
랜덤 워크 증분을 얻으려면 독립적이고 균등하게 분산되어야 합니다.
문제의 사실은 가격 증가가 정규 분포를 따르지 않는다는 것입니다. 그렇지 않으면 돈이 보장됩니다.
문제는 가격 증가분이 정규 분포를 따르지 않는다는 것입니다. 그렇지 않으면 돈이 보장됩니다.
어떤 증분이 비정상적입니까?
문제는 가격 증가분이 정규 분포를 따르지 않는다는 것입니다. 그렇지 않으면 돈이 보장됩니다.
가격 증분은 정규 분포로 간주될 수 있습니다. 이는 현실에 충분히 가깝지만 iid 이면 작동하지 않습니다. 가격 증분은 자유도가 4 또는 5인 t-분포로 간주할 수 있습니다. 이는 일반 증분의 가정보다 현실에 훨씬 가깝습니다.
결과 프로세스는 랜덤 워크가 됩니다. 여기서는 일반적으로 증분 분포에 관계없이 정규 분포가 보장되지만 정규성은 아무 소용이 없습니다. 랜덤 워크로 돈을 벌 수 없습니다. 가격 인상은 고정된 것으로 간주될 수 있지만 거래될 수는 없습니다. 가격을 거래할 수 있지만 랜덤 워크이며 프로세스가 고정적이지 않습니다. 적어도 이 주제의 맥락에서.
가격 증분은 정규 분포로 간주될 수 있습니다. 이것은 현실에 충분히 가깝지만 iid 이면 작동하지 않습니다. 가격 증분은 자유도가 4 또는 5인 t-분포로 간주할 수 있습니다. 이는 일반 증분의 가정보다 현실에 훨씬 가깝습니다.
결과 프로세스는 랜덤 워크가 됩니다. 여기서는 일반적으로 증분 분포에 관계없이 정규 분포가 보장되지만 정규성은 아무 소용이 없습니다. 랜덤 워크로 돈을 벌 수 없습니다. 가격 인상은 고정된 것으로 간주될 수 있지만 거래될 수는 없습니다. 가격을 거래할 수 있지만 랜덤 워크이며 프로세스가 고정적이지 않습니다. 적어도 이 주제의 맥락에서.
토론을 계속 진행하기 위해 약간의 논쟁을 해도 될까요? 제가 지금 무슨 말을 하고 싶은지 잘 모르겠습니다. 특히 너무 늦었기 때문에. 하지만 여전히... 어떤 값의 증분이 정규 분포를 따른다면, 이것은 이 값이 제한된다는 것을 의미합니다. (잘못된?)
이전 진술에서 내가 틀리지 않았다면 수량 값 세트에는 최대값과 최소값이 있습니다. 또한 값의 값이 최대값 또는 최소값에 가까울수록 평균을 향해 변화할 가능성이 높아집니다. 사용할 수 있는 법입니다.
추신 내가 공격하고 있다고 생각하지 마십시오. 나는 똑똑한 사람과 이야기하고 싶을 뿐입니다.
토론을 계속 진행하기 위해 약간의 논쟁을 해도 될까요? 제가 지금 무슨 말을 하고 싶은지 잘 모르겠습니다. 특히 너무 늦었기 때문에. 그러나 여전히 ... 일부 값의 증분이 정규 분포라면 이 값이 제한됨을 의미합니다. (잘못된?)
이전 진술에서 내가 틀리지 않았다면 수량 값 세트에는 최대값과 최소값이 있습니다. 또한 값의 값이 최대값 또는 최소값에 가까울수록 평균을 향해 변경될 가능성이 높아집니다. 사용할 수 있는 법입니다.
추신 내가 공격하고 있다고 생각하지 마십시오. 나는 똑똑한 사람과 이야기하고 싶을 뿐입니다.
아크사인 정리와 플레이어의 오류에 대해 들어보셨나요?
나는 의도적으로 편차의 상대성이론에 대해 물었다.
그것이 반환이라면 - 한 곡.
MA(x 마침표) - 또 다른 곡...
MA 대신 TrueDMA를 사용하면 완전히 다른 불협화음이 발생합니다.
;)
어디에서 이상을 얻었습니까?
내가 묻지 않는 사람들은 침묵합니다.
테마 가 있습니다 - 반대가 표시됩니다.
야 내...
:)
토론을 계속 진행하기 위해 약간의 논쟁을 해도 될까요? 제가 지금 무슨 말을 하고 싶은지 잘 모르겠습니다. 특히 너무 늦었기 때문에. 그러나 여전히 ... 일부 값의 증분이 정규 분포라면 이 값이 제한됨을 의미합니다. (잘못된?)
이전 진술에서 내가 틀리지 않았다면 수량 값 세트에는 최대값과 최소값이 있습니다. 또한 값의 값이 최대값 또는 최소값에 가까울수록 평균을 향해 변경될 가능성이 높아집니다. 사용할 수 있는 법입니다.
추신 내가 공격하고 있다고 생각하지 마십시오. 나는 똑똑한 사람과 이야기하고 싶을 뿐입니다.
당신은 확실히 틀렸다. 분포의 특성은 크기를 제한하는 것에 대해 아무 말도 하지 않습니다. 물론 몇 가지 예외가 있지만 일반적으로 그렇습니다. 분포 매개변수에 의해 제한이 부과됩니다. 예: 정규 분포 변환 ~N(0,1). 이것은 고정된 과정이며 크기 제한이 있으며 거의 4 또는 -4에 도달하지 않습니다.
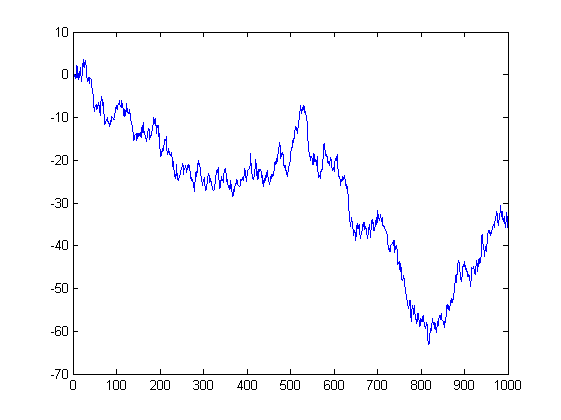

그리고 여기에 이러한 증분에서 나온 가격이 있습니다. 랜덤 산책입니다. 또한 정규 분포 ~N(0,sigma^2)를 갖지만 분산 매개변수는 일정하지 않지만 시간이 지남에 따라 증가합니다. 증분 수. 당연히 이 프로세스는 크기 제한이 없으며 동일한 확률로 모든 포인트를 방문합니다. 이것이 플레이어를 망치는 문제의 기초입니다. 만약 당신이 충분히 오랫동안(50:50) 절대적으로 공정한 게임을 한다면, 당신은 여전히 지게 될 것입니다. 왜냐하면. 조만간 이 곡선은 당신이 가진 돈보다 더 낮아질 것입니다.
그러나 1000번의 무작위 보행에서는 정규분포의 종 모양이 명확하게 보입니다.
그러나 평균으로 되돌리는 것에 대해 말하는 것은 완전히 다른 이야기입니다. 이것은 평균으로 되돌리는 과정입니다 - autoregressive(AR)
x(i) = a * x(i-1) + e(i). e(i) 변환 ~N(0,1), a < 1.
거래된 평균 회귀 프로세스를 발견했다면 양배추가 든 바구니를 끌 시간이 있습니다. 당연히 매개변수(평균으로의 회귀율(a))에 따라 다르지만 어쨌든 모든 것이 좋습니다.
그러나 1000번의 무작위 보행에서는 정규분포의 종 모양이 명확하게 보입니다.
당신은 히트 주파수로 조명해야합니다.
--
확장 이중 Tsar(log) 벨.
;)
не всякий увидит.
1000번째 판독값에 대한 히스토그램과 확률 뗏목이 있습니다.


증분이 정규화되었다는 사실에 근거하지만 정규분포의 합은 정규분포이다. 확인할 것도 없습니다.
1000번째 판독값에 대한 히스토그램과 확률 뗏목이 있습니다.
증분이 정규화되었다는 사실에 근거하지만 정규분포의 합은 정규분포이다. 확인할 것도 없습니다.
센크스!
좋은(또는 오히려 시각적으로 유용한) 작업입니다.