음, Neutron이 와서 모든 것을 제자리에 두었습니다. 그건 그렇고, 마케터는 첨도와 비대칭에 대해서도 이야기합니다.
해당 가우스 곡선은 어떤 방식으로든 구성할 수 있지만 여기서는 샘플 분산만 계산하고 매개변수 0과 시그마를 사용하여 가우스 곡선을 구성하는 것이 가장 쉽습니다. 그러면 실제 히스토그램과 이러한 가우시안 곡선의 차이가 나타납니다.
그건 그렇고, 이 가우스 근사치는 곡선 중앙(영점에서)의 실제 히스토그램보다 훨씬 낮아야 합니다.
유레인 너 얼마야 곱한 샘플?
한편, s.c.d. 강한 꼬리를 가진 분포의 경우 표본의 크기에 따라 달라지므로 여기서는 그렇게 간단하지 않습니다.
RMS는 전혀 건드리지 않고 완성된 플롯을 가져와 히스토그램에 세로로 맞도록 크기를 조정했습니다.
히스토그램은 Klos 차이의 분포(MO와 RMS가 있음)이며, 이러한 MO와 RMS는 위의 공식에 따라 빨간색 선을 만드는 데 사용되지만 히스토그램의 맨 아래에서 선이 손실되고 작은 절대값이 x는 히스토그램 y에 상응하는 요소를 구축하는 데 책임이 있으며, 비교를 위해 각 y 라인에 인수를 곱해야 했습니다.
참조 함수의 경우 분산 및 MO는 여러 따옴표에서 가져오고(여기에서도 계산됨) 참조의 절대값으로 동일한 조작이 수행됩니다. 여기에서 각 항을 계수에 추가해야 합니다 정점을 결합하기 위해.
내가 아는 한 참조 기능은 HP 기능입니다.
그렇다면 곱셈을 할 수 없다는 한 가지를 제외하고는 모든 것을 올바르게 수행한 것입니다. 피크를 결합하려는 욕구는 그래프의 실제 위치와 관련이 없습니다. 또한 곱하는 동안 HP 함수의 정규화를 위반합니다. 확률 >1을 원하십니까?
곱셈을 제거하고 그림을 다시 만들면 그래픽 너비가 다소 적절하게 일치합니다. 그러나 히스토그램은 중앙과 가장자리에서 더 높을 것이며, 이는 두 가지 주요 문제, 즉 더 큰 재발과 동시에 두꺼운 꼬리를 나타냅니다.
실례가 안된다면 이렇게 사진을 찍어보세요.
추신
이전 게시물에서 귀하의 문제를 이해합니다. HP의 정상화를 깨뜨릴 필요가 없습니다. 히스토그램에 적합한 척도를 찾는 것이 좋습니다. 동일한 정규화에서 나온 것입니다. 히스토그램의 모든 막대 높이를 더한 다음 각 막대를 해당 값으로 나누어야 합니다. 그 결과 히스토그램도 1로 정규화됩니다.
그렇다면 곱셈을 할 수 없다는 한 가지를 제외하고는 모든 것을 올바르게 수행한 것입니다. 피크를 결합하려는 욕구는 그래프의 실제 위치와 관련이 없습니다. 또한 곱하는 동안 HP 함수의 정규화를 위반합니다. 어떻게 >1 확률을 원하십니까?
곱셈을 제거하고 그림을 다시 만들면 그래픽 너비가 다소 적절하게 일치합니다. 그러나 히스토그램은 중앙과 가장자리에서 더 높을 것이며, 이는 두 가지 주요 문제, 즉 더 큰 재발과 동시에 두꺼운 꼬리를 나타냅니다.
실례가 안된다면 이렇게 사진을 찍어보세요.
추신
이전 게시물에서 귀하의 문제를 이해합니다. HP의 정상화를 깨뜨릴 필요가 없습니다. 히스토그램에 적합한 척도를 찾는 것이 좋습니다. 동일한 정규화에서 나온 것입니다. 히스토그램의 모든 막대 높이를 더한 다음 각 막대를 해당 값으로 나누어야 합니다. 그 결과 히스토그램도 1로 정규화됩니다.
글쎄, 그렇게 철자가 vlob이 아닙니다. 모든 것이 일찍 고쳐져야 합니다.
글쎄요, 규제가 전혀 없습니다. 둘 다 포인트 Multi=1.0/Point로 조정됩니다. 그렇지 않으면 칠면조는 그러한 작은 값을 보지 못합니다.
공포. 사람들은 너무 서두르는 말을 해서 나는 패자인 나로서는 여기에 속하지 않는다.
그리고 나는 읽고 있습니다. 나는 그들이 무엇에 동의할지 이해하려고 노력하고 있습니다.
이것이 다시 램이라면 문어에 연미복을 당기는 첫 번째 시도는 한 가지입니다. 실용적인 거라면 해볼게.
음, Neutron이 와서 모든 것을 제자리에 두었습니다. 그건 그렇고, 마케터는 첨도와 비대칭에 대해서도 이야기합니다.
해당 가우스 곡선은 어떤 방식으로든 구성할 수 있지만 여기서는 샘플 분산만 계산하고 매개변수 0과 시그마를 사용하여 가우스 곡선을 구성하는 것이 가장 쉽습니다. 그러면 실제 히스토그램과 이러한 가우시안 곡선의 차이가 나타납니다.
그건 그렇고, 이 가우스 근사치는 곡선 중앙(영점에서)의 실제 히스토그램보다 훨씬 낮아야 합니다.
유레인 너 얼마야 곱한 샘플?
한편, s.c.d. 강한 꼬리를 가진 분포의 경우 표본의 크기에 따라 달라지므로 여기서는 그렇게 간단하지 않습니다.
RMS는 전혀 건드리지 않고 완성된 플롯을 가져와 히스토그램에 세로로 맞도록 크기를 조정했습니다.
히스토그램은 Klos 차이의 분포(MO와 RMS가 있음)이며, 이러한 MO와 RMS는 위의 공식에 따라 빨간색 선을 만드는 데 사용되지만 히스토그램의 맨 아래에서 선이 손실되고 작은 절대값이 x는 히스토그램 y에 상응하는 요소를 구축하는 데 책임이 있으며, 비교를 위해 각 y 라인에 인수를 곱해야 했습니다.
참조 함수의 경우 분산 및 MO는 여러 따옴표에서 가져오고(여기에서도 계산됨) 참조의 절대값으로 동일한 조작이 수행됩니다. 여기에서 각 항을 계수에 추가해야 합니다 정점을 결합하기 위해.
내가 아는 한 참조 기능은 HP 기능입니다.
그렇다면 곱셈을 할 수 없다는 한 가지를 제외하고는 모든 것을 올바르게 수행한 것입니다. 피크를 결합하려는 욕구는 그래프의 실제 위치와 관련이 없습니다. 또한 곱하는 동안 HP 함수의 정규화를 위반합니다. 확률 >1을 원하십니까?
곱셈을 제거하고 그림을 다시 만들면 그래픽 너비가 다소 적절하게 일치합니다. 그러나 히스토그램은 중앙과 가장자리에서 더 높을 것이며, 이는 두 가지 주요 문제, 즉 더 큰 재발과 동시에 두꺼운 꼬리를 나타냅니다.
실례가 안된다면 이렇게 사진을 찍어보세요.
추신
이전 게시물에서 귀하의 문제를 이해합니다. HP의 정상화를 깨뜨릴 필요가 없습니다. 히스토그램에 적합한 척도를 찾는 것이 좋습니다. 동일한 정규화에서 나온 것입니다. 히스토그램의 모든 막대 높이를 더한 다음 각 막대를 해당 값으로 나누어야 합니다. 그 결과 히스토그램도 1로 정규화됩니다.
그리고 나는 읽고 있습니다. 나는 그들이 무엇에 동의할지 이해하려고 노력하고 있습니다.
이것이 다시 램이라면 문어에 연미복을 당기는 첫 번째 시도는 한 가지입니다. 실용적인 거라면 해볼게.
정규 분포에 없는 일련의 따옴표의 첫 번째 차이점이 무엇인지 식별하려고 합니다.
정규 분포에 없는 일련의 따옴표의 첫 번째 차이점이 무엇인지 식별하려고 합니다.
그리고 그것은 무엇을 줄 것입니까? 어떤 목표 설정입니까? "비정상" 영역을 식별하시겠습니까? 다시 - 왜?
("?????"만)))
그리고 그것은 무엇을 줄 것입니까? 어떤 목표 설정입니까? "비정상" 영역을 식별하시겠습니까? 다시 - 왜?
("?????"만)))
어떤 법칙에 따라 이상이 발현되는지 조사해보자.
내가 아는 한 참조 기능은 HP 기능입니다.
그렇다면 곱셈을 할 수 없다는 한 가지를 제외하고는 모든 것을 올바르게 수행한 것입니다. 피크를 결합하려는 욕구는 그래프의 실제 위치와 관련이 없습니다. 또한 곱하는 동안 HP 함수의 정규화를 위반합니다. 어떻게 >1 확률을 원하십니까?
곱셈을 제거하고 그림을 다시 만들면 그래픽 너비가 다소 적절하게 일치합니다. 그러나 히스토그램은 중앙과 가장자리에서 더 높을 것이며, 이는 두 가지 주요 문제, 즉 더 큰 재발과 동시에 두꺼운 꼬리를 나타냅니다.
실례가 안된다면 이렇게 사진을 찍어보세요.
추신
이전 게시물에서 귀하의 문제를 이해합니다. HP의 정상화를 깨뜨릴 필요가 없습니다. 히스토그램에 적합한 척도를 찾는 것이 좋습니다. 동일한 정규화에서 나온 것입니다. 히스토그램의 모든 막대 높이를 더한 다음 각 막대를 해당 값으로 나누어야 합니다. 그 결과 히스토그램도 1로 정규화됩니다.
글쎄, 그렇게 철자가 vlob이 아닙니다. 모든 것이 일찍 고쳐져야 합니다.
글쎄요, 규제가 전혀 없습니다. 둘 다 포인트 Multi=1.0/Point로 조정됩니다. 그렇지 않으면 칠면조는 그러한 작은 값을 보지 못합니다.
. 왼쪽 하단에는 확률 분포 밀도가 있고 오른쪽에는 대수 규모입니다.
분포가 정상이면 여기에 포물선이 있지만 "뚱뚱한" 꼬리 때문에 포물선이 없습니다. 원칙적으로 여기에서 최소 제곱법을 사용하여 가우스를 입력해야 합니다. 그러면 모든 것이 제자리에 들어갈 것입니다. 최적의 피팅을 위해 공식을 입력해야 합니다...
Sergey, 이중 로그는 어떻습니까? 뭔가 생각이 날 갉아먹는다 오늘은 첫날이 아니야...
겸손해서 다 확인하지는 않겠습니다 :)
Sergey, 이중 로그는 어떻습니까? 뭔가 생각이 날 갉아먹는다 오늘은 첫날이 아니야...
겸손해서 다 확인하지는 않겠습니다 :)
다음과 같이 나타납니다.
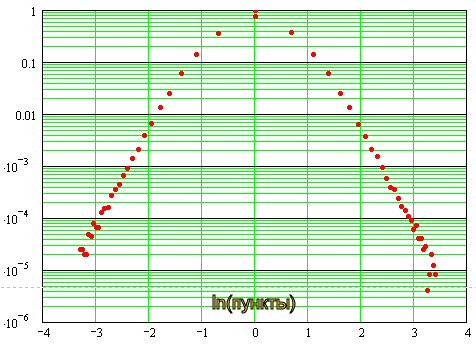
0에 가까우면 분포가 정규에 가깝고 직선 형태로 점근적임을 알 수 있으며, 이는 이중 로그 척도에서 "꼬리" 분포의 지수적 특성을 나타냅니다. 즉, 그들의 "무거움"에 대해.