선형 거래 시스템을 강화하세요

소개

오늘의 글에서는 중급 MQL5 프로그래머가 소위 지수 기법을 쉽게 구현하여 선형 거래 시스템(고정 랏)에서 더 많은 이익을 얻을 수 있는 방법을 보여줍니다. 지수화의 일반적인 용어는 여기에서 감수하는 위험에 따라 시장에 배치된 포지션의 크기 또는 수를 조정하는 통화 관리 모델을 언급하는 데 사용됩니다. 이는 그 결과 주식 곡선 성장이 포물선의 형태를 취하는 기하학적 또는 지수적이기 때문입니다. "선형"이라는 용어는 수학적 개념과 프로그래밍 개념의 중간인 현재 컨텍스트에서도 사용됩니다. 특히, Ralph Vince가 개발한 고정 분수 위치 크기 조정의 실용적인 MQL5 변형을 구현합니다.

그림 1. 수학 포물선

이제 자금 관리 모델에 대한 간략한 요약을 수행하고 Ralph Vince의 고정 분수 위치 크기 조정 변형을 구현하는 방법을 살펴보겠습니다. 준비가 되었나요? 거래 전략에서 더 많은 것을 얻을 수 있는 기회를 놓치지 마십시오!

1. 자금 관리 모델이란 무엇입니까?

간단히 말해서 자금 관리 모델은 포지션 규모, 손절매 사용, 마진 계산 및 거래 비용과 관련하여 결정을 내리는 개념적 프레임워크입니다. 많은 자금 관리 모델이 있습니다! 원하는 경우 고정 랏, 고정 분수, 고정 비율, 켈리 백분율 또는 유효 비용을 검색하여 이러한 고전적 프레임워크에 대한 지식을 심화할 수 있습니다. 제가 말했듯이 이 글은 고정 분수의 변형만 다룹니다.

1.2. 고정 분수

이 자금 관리 모델의 이면에 있는 아이디어는 관련 예상 위험에 따라 운영 규모를 조정하는 것입니다. 위험은 각 거래에서 순액의 동일한 부분입니다. 

고정 분수 포지션 사이징의 계약 수에 대한 방정식은 다음과 같습니다.

N = f * 주식 / 거래 위험

N은 계약 수, f 는 고정 분수(0과 1 사이의 숫자), 자본은 계정 자본의 현재 가치입니다. , 그리고 거래 위험은 계약 수가 계산되는 계약당 거래의 위험입니다. 이 모델에 대한 자세한 내용은 Michael R. Bryant가 작성한 Fixed Fractional Position Sizing 글을 참조하세요.

고정 분수 모델의 흥미로운 속성은 작업의 크기가 계정의 순잔액에 비례하여 유지되기 때문에 이론적으로 모든 자본을 잃는 것이 불가능하다는 것입니다. 파멸의 위험은 0입니다. 반면에 위험 자본 비율이 낮기 때문에 연속적인 영업 승패는 이익 곡선에 극적인 영향을 미치지 않습니다.

2. 거래 시스템에 고정 분수 추가

2.1. 선형 거래 시스템 사용

물론 저위험 지수의 힘을 경험하기 위해서는 우선 선형 거래 시스템이 필요합니다! 이 시스템은 말하자면 전력 기반 역할을 할 것입니다. 선형 시스템이란 일정 기간 동안 승자가 되고 자기 자본 곡선이 직선처럼 보이는 거래 시스템을 의미합니다. 예를 들어 HawaiianTsunamiSurfer는 Code Base에서 사용할 수 있는 이른바 선형 거래 시스템입니다. 주식 곡선은 2012년 1월부터 2012년 3월까지 직선처럼 보입니다.

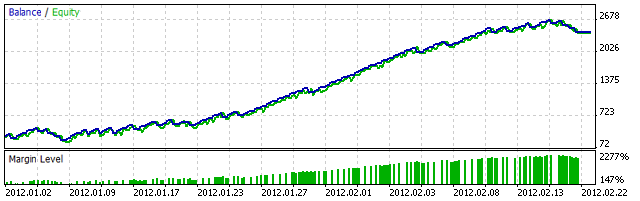
그림 2. 2012년 1월부터 2012년 3월까지의 HawaiianTsunamiSurfer의 주식 곡선

이 글의 목적은 선형 거래 시스템을 처음부터 개발하는 것이 아니라 시스템에서 더 많은 이점을 얻을 수 있도록 필요한 도구를 제공하는 것입니다. 따라서 이제부터는 개체지향 패러다임에서 이미 이와 같은 거래 시스템을 개발했다고 가정하겠습니다. 이 경우 아래에서 설명하는 OO 조각을 추가해야 합니다.

2.2. 시스템의 성능을 높이는 핵심 MQL5 클래스, CEvolution

따라서 다시 한 번 객체 지향 접근 방식을 사용하여 EA를 코딩합니다. 먼저 또 다른 MQL5 OOP 클래스 및 자동 뉴스 거래자 구축 글을 읽고 이 OO 방식으로 작동하기 위한 기술적 기반을 얻는 것이 좋습니다. 이미 이 작업을 수행했다면 해당 글에서 논의된 디자인에 CEvolution이라는 매우 중요한 요소가 포함되어 있다는 점에 유의하십시오. 이를 통해 주어진 순간의 로봇 상태, 수행된 작업 이력 등과 같은 중요한 시간 정보를 추적할 수 있습니다.

이번에는 돈을 관리하는 데 필요한 논리를 CEvolution으로 코딩합니다. 위험 고정 부분은 일정하지 않고 가변적이라는 데 우리 모두 동의하는 형평성에 비례하므로 이 논리적 요소는 CEvolution으로 코딩해야 합니다. 또는 간단히 말해서, 주식 곡선 기울기가 시간이 지남에 따라 진화함에 따라 이 모든 것이 구현되어야 하는 CEvolution입니다. 이것이 우리의 객체 지향 디자인의 추상적인 아이디어입니다. 다음 OO 클래스를 객체 지향 스타일 거래 시스템과 통합하기 위한 연습으로 남겨둡니다.

클래스 CEvolution.mqh::

//+------------------------------------------------------------------+
//|                                                   CEvolution.mqh |
//|                               Copyright © 2013, Jordi Bassagañas |
//+------------------------------------------------------------------+
#include <Mine\Enums.mqh>
//+------------------------------------------------------------------+
//| CEvolution Class                                                 |
//+------------------------------------------------------------------+
class CEvolution
  {
protected:
   ENUM_STATUS_EA                   m_status;            // The current EA's status
   ENUM_EXP_EQUITY_CURVE_LEVEL      m_expEquityLevel;    // The current exponential equity level
   double                           m_originalEquity;    // The original equity value
   double                           m_lotSize;           // The current lot size

public:
   //--- Constructor and destructor methods
                                    CEvolution(ENUM_STATUS_EA status,ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level);
                                    ~CEvolution(void);
   //--- Getter methods
   ENUM_STATUS_EA                   GetStatus(void);
   ENUM_EXP_EQUITY_CURVE_LEVEL      GetExpEquityLevel(void);
   double                           GetOriginalEquity(void);
   double                           GetLotSize(void);
   //--- Setter methods
   void                             SetStatus(ENUM_STATUS_EA status);
   void                             SetExpEquityLevel(ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level);
   void                             SetOriginalEquity(double equity);
   void                             SetLotSize(double size);
   //--- CEvolution specific methods
   double                           CalcEquityGrowth(double currentEquity);
   void                             RefreshExpEquityLevel(double currentEquity);
   void                             RefreshLotSize();
  };
//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CEvolution::CEvolution(ENUM_STATUS_EA status,ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level)
  {
   m_status=status;
   m_expEquityLevel=exp_equity_level;
   RefreshLotSize();
   m_originalEquity=AccountInfoDouble(ACCOUNT_EQUITY);
  }
//+------------------------------------------------------------------+
//| Destructor                                                       |
//+------------------------------------------------------------------+
CEvolution::~CEvolution(void)
  {
  }
//+------------------------------------------------------------------+
//| GetStatus                                                        |
//+------------------------------------------------------------------+
ENUM_STATUS_EA CEvolution::GetStatus(void)
  {
   return m_status;
  }
//+------------------------------------------------------------------+
//| GetExpEquityLevel                                                |
//+------------------------------------------------------------------+
ENUM_EXP_EQUITY_CURVE_LEVEL CEvolution::GetExpEquityLevel(void)
  {
   return m_expEquityLevel;
  }
//+------------------------------------------------------------------+
//| GetEquity                                                        |
//+------------------------------------------------------------------+
double CEvolution::GetOriginalEquity(void)
  {
   return m_originalEquity;
  }
//+------------------------------------------------------------------+
//| GetLotSize                                                       |
//+------------------------------------------------------------------+
double CEvolution::GetLotSize(void)
  {
   return m_lotSize;
  }
//+------------------------------------------------------------------+
//| SetStatus                                                        |
//+------------------------------------------------------------------+
void CEvolution::SetStatus(ENUM_STATUS_EA status)
  {
   m_status=status;
  }
//+------------------------------------------------------------------+
//| SetExpEquityLevel                                                |
//+------------------------------------------------------------------+
void CEvolution::SetExpEquityLevel(ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level)
  {
   m_expEquityLevel=exp_equity_level;
  }
//+------------------------------------------------------------------+
//| SetEquity                                                        |
//+------------------------------------------------------------------+
void CEvolution::SetOriginalEquity(double equity)
  {
   m_originalEquity=equity;
  }
//+------------------------------------------------------------------+
//| SetLotSize                                                       |
//+------------------------------------------------------------------+
void CEvolution::SetLotSize(double lot_size)
  {
   m_lotSize=lot_size;
  }
//+------------------------------------------------------------------+
//| CalcEquityGrowth                                                 |
//+------------------------------------------------------------------+
double CEvolution::CalcEquityGrowth(double currentEquity)
  {
   return NormalizeDouble(currentEquity * 100 / m_originalEquity - 100,2);
  }
//+------------------------------------------------------------------+
//| RefreshExpEquityLevel                                            |
//+------------------------------------------------------------------+
void CEvolution::RefreshExpEquityLevel(double currentEquity)
  {
   double growth = CalcEquityGrowth(currentEquity);
   //--- is the current equity less than 10% of the original amount?
   if(growth <= 10)
   {
      SetExpEquityLevel(LEVEL_ONE);
   }
   //--- is the current equity more than 10% of the original amount and less than 20%?
   else if(growth > 10 && growth <= 20)
   {
      SetExpEquityLevel(LEVEL_TWO);
   }
   //--- is the current equity more than 20% of the original amount and less than 30%?
   else if(growth > 20 && growth <= 30)
   {
      SetExpEquityLevel(LEVEL_THREE);
   }
   //--- is the current equity more than 30% of the original amount and less than 40%?
   else if(growth > 30 && growth <= 40)
   {
      SetExpEquityLevel(LEVEL_FOUR);
   }
   //--- is the current equity more than 40% of the original amount and less than 50%?
   else if(growth > 40 && growth <= 50)
   {
      SetExpEquityLevel(LEVEL_FIVE);
   }
   //--- is the current equity more than 50% of the original amount and less than 60%?
   else if(growth > 50 && growth <= 60)
   {
      SetExpEquityLevel(LEVEL_SEVEN);
   }
   //--- is the current equity more than 60% of the original amount and less than 70%?   
   else if(growth > 60 && growth <= 70)
   {
      SetExpEquityLevel(LEVEL_EIGHT);
   }
   //--- is the current equity more than 70% of the original amount and less than 80%?   
   else if(growth > 70 && growth <= 80)
   {
      SetExpEquityLevel(LEVEL_NINE);
   }
   //--- is the current equity more than 90% of the original amount?
   else if(growth > 90)
   {
      SetExpEquityLevel(LEVEL_TEN);
   }
  }
//+------------------------------------------------------------------+
//| RefreshLotSize                                                   |
//+------------------------------------------------------------------+
void CEvolution::RefreshLotSize()
  {
   switch(m_expEquityLevel)
   {
      case LEVEL_ONE:
         SetLotSize(0.01);
         break;
         
      case LEVEL_TWO:
         SetLotSize(0.02);
         break;
         
      case LEVEL_THREE:
         SetLotSize(0.03);
         break;
         
      case LEVEL_FOUR:
         SetLotSize(0.04);
         break;
         
      case LEVEL_FIVE:
         SetLotSize(0.05);
         break;
         
      case LEVEL_SIX:
         SetLotSize(0.06);
         break;
         
      case LEVEL_SEVEN:
         SetLotSize(0.07);
         break;

      case LEVEL_EIGHT:
         SetLotSize(0.08);
         break;
         
      case LEVEL_NINE:
         SetLotSize(0.09);
         break;
         
      case LEVEL_TEN:
         SetLotSize(0.1);
         break;
   }
  }
//+------------------------------------------------------------------+

이제 이 클래스의 몇 가지 중요한 부분에 대해 설명하겠습니다! 

Expert Advisor가 생성되면 원래 자기자본 곡선의 값이 m_originalEquity에 저장됩니다.

//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
CEvolution::CEvolution(ENUM_STATUS_EA status,ENUM_EXP_EQUITY_CURVE_LEVEL exp_equity_level)
  {
   m_status=status;
   m_expEquityLevel=exp_equity_level;
   RefreshLotSize();
   m_originalEquity=AccountInfoDouble(ACCOUNT_EQUITY);
  }

CEvolution::CalcEquityGrowth 방법은 항상 원래 값을 기준으로 주식 곡선의 성장을 계산하기 위한 것입니다.

//+------------------------------------------------------------------+
//| CalcEquityGrowth                                                 |
//+------------------------------------------------------------------+
double CEvolution::CalcEquityGrowth(double currentEquity)
  {
   return NormalizeDouble(currentEquity * 100 / m_originalEquity - 100,2);
  }

마지막으로, CEvolution::RefreshExpEquityLevel 은 매 틱마다 자기자본 수준을 새로 고치기 위한 것이며(자본 성장에 절대적으로 의존하는 방식을 관찰하십시오) CEvolution::RefreshLotSize는 모든 틱에 대한 랏을 새로 고치기 위한 것입니다. EA의 OnTick 에서 해당 정보를 다음과 같이 새로 고쳐야 하기 때문입니다.

GetEvolution().RefreshExpEquityLevel(AccountInfoDouble(ACCOUNT_EQUITY));
GetEvolution().RefreshLotSize();

그런데 이 솔루션을 사용하려면 다음 사용자 지정 MQL5 열거를 사용해야 합니다.

//+------------------------------------------------------------------+
//| Exponential equity curve level enumeration                       |
//+------------------------------------------------------------------+
enum ENUM_EXP_EQUITY_CURVE_LEVEL
  {
   LEVEL_ONE,
   LEVEL_TWO,
   LEVEL_THREE,
   LEVEL_FOUR,
   LEVEL_FIVE,
   LEVEL_SIX,
   LEVEL_SEVEN,
   LEVEL_EIGHT,
   LEVEL_NINE,
   LEVEL_TEN
  };

우리는 이 구현이 Fixed Fractional의 변형이라고 말합니다. 실제로 몇 가지 특이성을 도입하기 때문입니다. 예를 들어, 주식 곡선은 소위 수준 10에 도달할 때까지 기하급수적으로 증가하고 그 이후에는 시스템이 선형이 됩니다. 그럼에도 불구하고 CEvolution은 자본 곡선에 비례하여 포지션의 크기를 지속적으로 증가시킨다는 기본 아이디어를 유지합니다.

2.3. 고정 분수 결정 내리기

위의 모든 사항을 통해 로봇의 현재 상태에 따라 이미 자금 관리 결정을 내릴 수 있습니다.

EA의 OnTick 방법 어딘가:

switch(GetEvolution().GetStatus())
     {
      case BUY:

         tp = ask + m_takeProfit * _Point;
         sl = bid - m_stopLoss * _Point;

         GetTrade().PositionOpen(GetBrain().GetSymbol(),ORDER_TYPE_BUY,m_evolution.GetLotSize(),ask,sl,tp);
         
         break;

      case SELL:

         sl = ask + m_takeProfit * _Point;
         tp = bid - m_stopLoss * _Point;

         GetTrade().PositionOpen(GetBrain().GetSymbol(),ORDER_TYPE_SELL,m_evolution.GetLotSize(),bid,sl,tp);
         
         break;

      case DO_NOTHING:

         // Nothing...

         break;
     }

새로운 지수 시스템의 이름을 ExponentialHawaiian으로 변경했습니다.

3. 지수 시스템 백테스트

위에서 설명한 OO 로직을 시스템에 추가했으면 테스트를 실행하는 것을 잊지 마십시오! 이제 HawaiianTsunamiSurfer의 고정 분수 변형인 ExponentialHawaiian을 백테스트하고 있습니다.

그림 3. 2012년 1월부터 2012년 3월까지 ExponentialHawaiian의 주식 곡선

기본 시스템이 선형으로 유지되는 동안 위의 곡선은 기하급수적으로 유지됩니다. 이 조건이 더 이상 사실이 아닌 경우 시스템은 이론적인 파멸의 위험과 함께 불안정해집니다.

결론

오늘 우리는 고정 랏 자금 관리 모델을 구현하는 선형 거래 시스템을 지수력으로 올려 더 많은 이익을 얻는 방법을 배웠습니다.

우리는 몇 가지 고전적인 자금 관리 모델(고정 랏, 고정 분수, 고정 비율, 켈리 비율, 유효 비용)을 제시하는 것으로 시작했으며 작업 규모가 계정의 순잔액에 비례하여 유지되는 단순한 모델인 고정 분수에 집중하기로 결정했습니다. 마지막으로 우리는 일정 기간 동안 선형 결과를 보여주는 거래 시스템을 선택하고 MQL5에서 Fixed Fractional의 변형을 구현했으며 MetaTrader의 Strategy Tester에서 시작한 결과를 보여주었습니다.

다시 한 번, 우리는 Expert Advisors를 코딩하기 위해 객체 지향 접근 방식을 취했습니다. 먼저 또 다른 MQL5 OOP 클래스 및 자동 뉴스 트레이더 구축 글을 읽고 이 OO 방식으로 작업하기 위한 기술적 기반을 얻는 것이 좋습니다.