Vinceによるロット計算

新しいコメント

Victor Nikolaev 2011.08.14 03:05

から移植されました。

ローマン 14.08.2011 06:37

R.Vinceの方法を使って幾何平均法で最適なf（ロットボリューム計算用）を探しているのですが、皆さん、アドバイスをお願いします。

課題：注文履歴を調べ、0.01から1までf=0.01の増分で、TWRが最大となる最適値を求める。

という2つの式があり、トレードの最大損失の値はD=-458 であることが知られています。

どの列挙サイクル、特に最適なfを見つけるために、さらに、コード内の場所を整理する。

以下は、int deinit() の開始コードです。ストラテジーテスターにちゃんと利益について印刷される。

//+------------------------------------------------------------------+
//| expert deinitialization function                                 |
//+------------------------------------------------------------------+
int deinit()
  {
//--- Расчет оптимального f ---

   double SUMM, MUL, HPR, TWR, G;   
   double D=-458;
   int orderIndex;
   for (orderIndex = (OrdersHistoryTotal() - 1); orderIndex >= 0; orderIndex--)
   {   
      if (!OrderSelect(orderIndex, SELECT_BY_POS, MODE_HISTORY))
      {
         Print("Ошибка при доступе к исторической базе (",GetLastError(),")");
         continue;
      }
   
      if ((OrderSymbol() != Symbol()) || (OrderMagicNumber() != magic) || (OrderCloseTime()==0))
      {
         continue;
      }  
     
         int lastType = OrderType();
         double lastLots = OrderLots();
         double lastProfit = OrderProfit() + OrderSwap(); 
         SUMM=SUMM+lastProfit;    
    }           
    
  Print("Профит = ", SUMM);  
  
  return(0);
  }

Роман 2011.08.14 09:09 #1

Vinin:

から移管されました。

R. Vince氏の著書にあるように、最適なfを計算するために、次のようなfを作りました。

//---------переменные для расчета лота по оптимальному f Ральфа Винса
int Mas_Outcome_of_transactions [10000]; // Массив профитов/убытков закрытых позиций
extern double D = -628;                  // максимальный убыток по сделке

//+------------------------------------------------------------------+
//| expert deinitialization function                                 |
//+------------------------------------------------------------------+
int deinit()
  {
//----
  if(Monitor==true)
    {
    for(int a=0;a<=3;a++)
      {
      string N=DoubleToStr(a,0);
      ObjectDelete(N);
      } 
    }
//----
//--- Расчет оптимального f ---
   int Qnt=0;                                          // Счётчик количества ордеров   
   ArrayInitialize(Mas_Outcome_of_transactions,0);     // Обнуление массива
   double f=0.01, SUMM, MUL, HPR, TWR_Rez=0, TWR=1.0, G;
   int orderIndex;
   for (orderIndex = 0; orderIndex<OrdersHistoryTotal(); orderIndex++)
   {   
      if (!OrderSelect(orderIndex, SELECT_BY_POS, MODE_HISTORY))
      {
         Print("Ошибка при доступе к исторической базе (",GetLastError(),")");
         continue;
      }
   
      if ((OrderSymbol() != Symbol()) || (OrderMagicNumber() != magic) || (OrderCloseTime()==0))
      {
         continue;
      }  
         Qnt++;                               // увеличиваем счетчик закрытых ордеров
         int lastType = OrderType();
         double lastLots = OrderLots();
         double lastProfit = OrderProfit() + OrderSwap(); 
        
         Mas_Outcome_of_transactions[Qnt] = lastProfit; // Заполняем массив профитом/лоссом по всем закрытым позициям 
         SUMM=SUMM+lastProfit;    
         //TWR = TWR*(1+f*(-lastProfit/(D)));
    }           
 //  Print("Закрытых позиций = ", Qnt, " Профит/лосс = ", SUMM);  
 
   for (f = 0.01; f<=1.0; f=f+0.01)//цикл перебора переменной f для поиска оптимального ее значения,при котором TWR-максимально
     {  
          
          for ( orderIndex = 1;orderIndex<Qnt; orderIndex++) //при заданной f проходим по всем закрытым ордерам
            {                                                // и считаем относительный конечный капитал (TWR)
             TWR = TWR*(1+f*(-Mas_Outcome_of_transactions[orderIndex]/(D))); // TWR - это произведение всех HPR
             //if (TWR>TWR_Rez) {TWR_Rez = TWR; Print(" TWR = ",TWR_Rez, " при f = ", f);}  
             //   else break;       
            }
          if (TWR>TWR_Rez) {
              TWR_Rez = TWR;
              G=MathPow (TWR_Rez, 0.001988); // 1/503 сделки по данной торговой системе, как в книжке: в степени 1/N 
              Print(" TWR = ",TWR_Rez," G = ",G, " при f = ", f);} // если текущий TWR > результирующего, 
              else break;    // то результирующий делаем равным текущему, иначе переходим на след итерацию цикла по f                                  
      }      
             
   Print("Закрытых позиций = ", Qnt, " Нетто Профит/лосс = ", SUMM, " У последней ",Qnt, " закрытой позы профит/лосс = ", 
        Mas_Outcome_of_transactions[Qnt]);     
  
  return(0);
  }

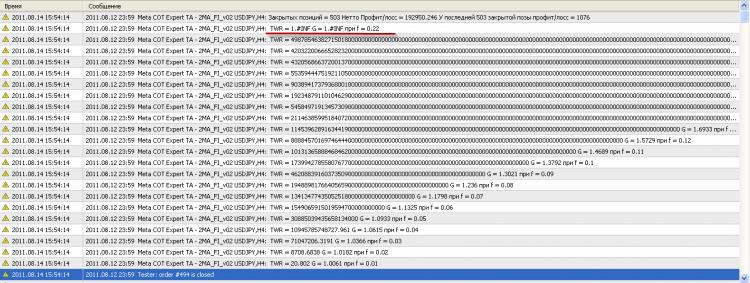
EAをテストした後のログブックで、上から2行目のTWR=1.#INFは どういう意味か教えてください。

何ですか？- アウトオブレンジダブル ?

この場合、最適なfはどのように算出するのでしょうか？

Victor Nikolaev 2011.08.14 09:22 #2

Roman.:

R. Vinceの著書に従って、最適なfを計算するために、以下のような関数を作りました。

EAをテストした後のログブックで、上から2行目のTWR=1.#INFという のはどういう意味か、教えてください。

何ですか？- アウトオブレンジダブル？

その場合、最適なfはどのように算出するのでしょうか？

3289	ロッシュ 2005.10.26 20:49 また、「1.INF」「1.IND」という数字は、モジュロ値が高すぎるか、0/0型の未定義値である（と私は考えている）。

4464	スラワ 2005.10.27 09:59 また、「1.INF」「1.IND」は、モジュール内の値が大きすぎるか、0/0型の未定義値（だと思う）のどちらかです。浮動小数点数のオーバーフロー(1.INF)と倍数のオーバーフロー(1.IND)です。

Лекарь Центозависимых 2011.08.14 09:23 #3

Anton Trefolevhttp://forum.alpari.ru/member.php?u=56027 最適なfを研究していたので、彼に聞いてみるといい。かつて（私の記憶では）3ヶ月で11000％上げた無名の人。そして、一夜漬けの十字架に広がりを持たせることで、彼への酸素を遮断したのです。それでも彼は10万円以上まで口座を増やしたが、その後、口座を閉鎖せざるを得なくなった。

Роман 2011.08.14 09:36 #4

Vinin:

3289	ロッシュ 2005.10.26 20:49 また、「1.INF」「1.IND」という数字は、モジュロ値が大きすぎるか、0/0のような未定義の値（だと思う）を意味しています。

4464	スラワ 2005.10.27 09:59 また、「1.INF」「1.IND」という数字は、モジュロ値が高すぎるか、0/0型の未定義値という意味です（そうだと思います）。これは浮動小数点数のオーバーフロー(1.INF)と2桁目のオーバーフロー(1.IND)です。

そこがミソで、割り算はなく、掛け算だけ（ヴィンスの公式を使用、以上） です。

つまり、mqlを使っても、この問題（TWRの正しい計算）は解けないのですね？

I.e. ddlやmatcadなどを使って？

Роман 2011.08.14 09:45 #5

Vinin:

3289	ロッシュ 2005.10.26 20:49 また、「1.INF」「1.IND」という数字は、モジュロ値が大きすぎるか、0/0のような未定義の値（だと思う）を意味しています。

4464	スラワ 2005.10.27 09:59 また、「1.INF」「1.IND」の数値は、モジュロ値が高すぎるか、0/0型の未定義値である（と私は考えています）。これは浮動小数点数のオーバーフロー(1.INF)と2桁目のオーバーフロー(1.IND)です。

オーダーフロート(1.INF)がオーバーフローした場合はどうなるのでしょうか？

fループの後続の繰り返しは、現在の結果で中断されるのでしょうか、それともループはカウントし続けるのでしょうか？TWRの数値に興味があるのではなく、累積総TWRとの掛け算で得られるfの数値に興味があるのです。

このコードの一部では

for (f = 0.01; f<=1.0; f=f+0.01)//цикл перебора переменной f для поиска оптимального ее значения,при котором TWR-максимально
     {  
          
          for ( orderIndex = 1;orderIndex<Qnt; orderIndex++) //при заданной f проходим по всем закрытым ордерам
            {                                                // и считаем относительный конечный капитал (TWR)
             TWR = TWR*(1+f*(-Mas_Outcome_of_transactions[orderIndex]/(D))); // TWR - это произведение всех HPR                
            }
          if (TWR>TWR_Rez) {
              TWR_Rez = TWR;
              G=MathPow (TWR_Rez, 0.001988); // 1/503 сделки по данной торговой системе, как в книжке: в степени 1/N 
              Print(" TWR = ",TWR_Rez," G = ",G, " при f = ", f);} // если текущий TWR > результирующего, 
              else break;    // то результирующий делаем равным текущему, иначе переходим на след итерацию цикла по f                                  
      }

Victor Nikolaev 2011.08.14 09:58 #6

Roman.:

要は割り算がなく、掛け算だけ（ヴィンスの公式を使えば、ですが）。

では、mqlはこの問題（TWRの正しい計算）を解決できないのですか？

I.e. ddlやmatcadなどを使って解く？

乗算もオーバーフローを起こすことがあります。

Роман 2011.08.14 10:01 #7

Vinin:

掛け算の時もオーバーフローすることがあるんですね。

それは分かっています。しかし、それではその幾何平均法を用いて最適なfを計算するにはどうしたらよいのでしょうか。私はすべての数式を、すべて正しくコードに書きました。

Victor Nikolaev 2011.08.14 10:06 #8

Roman.:

それは分かっています。では、その幾何平均法を用いて最適なfを計算するにはどうすればよいのでしょうか。計算式は全て正しくコードに書きました。

おそらく、最適化について考える必要があるのでしょう。計算のバリエーションを見つけることができます。

Maxim Zaguzov 2011.08.14 10:17 #9

TWRと前回値（TWR_Rez）ではなく、それらの幾何平均GとあるG_Rezを比較するのはどうでしょうか。結局、数_1の次数Kの根が数_2の同じ次数Kの根より大きければ、数_1は数_2より大きい ということになるのです:))))

また、積を要素に分割し（なぜ分割するのか）、各要素から根を求めると、すでに根（変数G）を計算しているので、オーバーフローすることはありません。結局、積の根は、その因子の根の積に等しい のです:)))

計算時間は増えますが、オーバーフローすることもなく、大騒ぎすることもないでしょう。また、計算精度の向上も顕著です。

TWR変数を表示したい場合は、int型の追加変数にそのサイズを格納し、PrintでTWRのサイズを表示するなどの工夫をします。"89605994539435e+1234121".でも、必要ですか？

TheXpert 2011.08.14 10:18 #10

Roman.:
それは分かっています。では、その幾何平均法を用いて最適なfを計算するにはどうすればよいのでしょうか。計算式はすべてコードに正しく書いてあるんだけどね。

幾何平均の計算をいじってみないとわからない。

1 2 3 4 5 6 7 8 9 10 11 12

新しいコメント