"New Neural "は、MetaTrader 5プラットフォーム用のオープンソース・ニューラルネットワークエンジンプロジェクトです。 - ページ 56 1...495051525354555657585960616263...100 新しいコメント Ilyas 2011.11.17 18:23 #551 ウラン です。そう、それこそが私が知りたかったことなのです。mql5へ SZ 現時点での最大の関心事は、データをCPUの特殊な配列にコピーする必要があるのか、通常の関数で配列をパラメータとして渡すことがサポートされるのか、ということです。この問いかけは、プロジェクト全体を根本から変えてしまうかもしれません。ZZY OpenCLのAPIを提供するだけの計画なのか、それとも独自のラッパーで包む計画なのか、お答えください。 1) GPUメモリのことでしたら、はい、ユーザーアレイをコピーする(in/out)特別な関数があるでしょう。 2) ラッパーがあり、HW GPUのみサポートされる(OpenCL 1.1対応)予定。 複数のGPUを選択する場合は、端末の設定によってのみ可能です。 OpenCLは同期的に使用されます。 Andrey Dik 2011.11.17 18:31 #552 ウラン です。そう、それこそが私が知りたかったことなのです。mql5へ SZ 現時点での最大の関心事は、データをCPUの特殊な配列にコピーする必要があるのか、通常の関数で配列をパラメータとして渡すことがサポートされるのか、ということです。この問いかけは、プロジェクト全体を根本から変えてしまうかもしれません。ZZZY OpenCLのAPIを提供するだけの予定なのか、それとも独自のラッパーで包む予定なのか、お答えください。で判断する。mql5 です。 実際には、サードパーティのDLLをプラグインすることなく、OpenCL.dllのライブラリ関数を直接使用することができます。OpenCL.dllの関数は、コンパイラが呼び出し自体をリダイレクトしながら、あたかもMQL5のネイティブ関数のように利用できるようになります。このことから、OpenCL.dllの機能は、現在すでに敷設可能(ダミーコール)であると判断できる。Renatさん、 mql5 さん、「環境」は正しく理解できましたか? Ilyas 2011.11.17 18:41 #553 ジュで判断する。OpenCL.dllの関数は、あたかもMQL5の ネイティブ関数の ように使うことができ、コンパイラ自身が呼び出しをリダイレクトします。このことから、OpenCL.dllの機能は、現在すでに敷設可能(ダミーコール)であると判断できる。Renatさん、 mql5 さん、私の「状況」は合っていますか? OpenCLを使った開発作業。OpenCL.dllを直接使用する場合とは異なる点があります。 Mykola Demko 2011.11.17 20:29 #554 ここまでは、このプロジェクトのスキームです。 オブジェクトは長方形、メソッドは楕円です。 Mykola Demko 2011.11.17 21:10 #555 処理方法は4つに分類されます。метод параллельных расчётов метод последовательных расчётов метод расчётов активатора метод расчётов операторов задержки これら4つのメソッドは、全層にわたる処理全体を記述し、メソッドはメソッドオブジェクトを通じて処理に取り込ま れ、ベースクラスから継承され、ニューロンの種類に応じて必要に応じてオーバーロードされる。 TheXpert 2011.11.17 23:43 #556 ウラン です。ニコライ 「早すぎる最適化は諸悪の根源」というキャッチフレーズをご存じですね。OpenCLのことはとりあえず忘れてください。 OpenCLがなくてもまともなことができるようになります。特に、まだ利用できない場合は、必ずトランスポーズする時間があります。 Mykola Demko 2011.11.18 01:39 #557 TheXpert です。ニコライさん、「早すぎる最適化は諸悪の根源」という言葉がありますよね。OpenCLのことはとりあえず忘れてください。OpenCLがなくても、まともなものが書けるはずです。いつでも切り替えられる。 それに、まだ内製化された機能はないんだ。そう、よく言われることで、前回もほぼ同意見だったのですが、分析してみると、ただ企画するだけではGPUのために再設計することはできない、非常に特殊なニーズを持っていることがわかりました。GPUを使わないのであれば、ニューロン内部の演算と、必要なメモリセルへの演算データの割り当ての両方を担当するNeuronオブジェクトを作り、共通の祖先からクラスを継承することで、必要なニューロンタイプなどを簡単に接続できるようにするのが理にかなっていると思います。 しかし、少し頭を働かせてみると、このやり方ではGPUの計算が完全に崩れ、生まれてくる子どもは這いずり回る運命にあることがすぐにわかったのです。しかし、上記の私の投稿はあなたを混乱させたと思われます。 そこでの「並列計算法」とは、入力と重みをin*wgで掛け合わせるというかなり具体的な操作のことで、「連続計算法」とは、sum+=a[i]といったような操作のことです。ただ、将来のGPUとの親和性を考えて、ニューロンから操作を派生させて、レイヤーオブジェクトで1つの動きにまとめ、ニューロンは「どこからどこまでを取るか」という情報のみを提供することを提案します。 Vladimir 2011.11.19 23:51 #558 講義1はこちらhttps://www.mql5.com/ru/forum/4956/page23 レクチャー2はこちらhttps://www.mql5.com/ru/forum/4956/page34 レクチャー3はこちらhttps://www.mql5.com/ru/forum/4956/page36 レクチャー4はこちらhttps://www.mql5.com/ru/forum/4956/page46 第5講(最終回)。スパース符号化 このテーマが一番面白いので、これから少しずつ書いていこうと思います。だから、時々この記事をチェックするのを忘れないでください。 一般的には、直近のN本の価格提示(ベクトルx)を基底関数(行列Aの 系列)への線形分解として提示することが課題です。 ここで、s は線形変換の係数で、ニューラルネットワークの次の層(例えば SVM)の入力として見つけたいものです。ほとんどの場合、基底関数Aは分かって いる、つまり、あらかじめ選んでいるのである。異なる周波数のサインやコサイン(フーリエ変換)、ガボール関数、Hammotons、ウェーブレット、カーレット、多項式、その他の関数が使用できます。これらの関数があらかじめ分かっている場合、スパースコーディングは、係数sの ほとんどが0になるようなベクトル(スパースベクトル)を求めることになります。ほとんどの情報信号は、信号のサンプル数より少ない数の基底関数で記述される構造を持っているという考え方である。信号のスパース記述に含まれるこれらの基底関数は、信号の分類に必要な特徴である。 元の情報の排出される線形変換を求める問題をCompressed Sensing (http://ru.wikipedia.org/wiki/Compressive_sensing) という。一般に、この問題は次のように定式化される。 sのL0ノルムを最小化する、As = xに従う。 ここで、L0ノルムはベクトルsの 非ゼロ値の数に等しい。この問題を解決する最も一般的な方法は、L0ノルムをL1ノルムに置き換えることであり、これは基底追求法(https://en.wikipedia.org/wiki/Basis_pursuit)の基本である。 のL1ノルムを最小化し、As = x とする。 ここで、L1ノルムは|s_1|+|s_2|+|...+|s_L|として計算される。この問題は、線形最適化に還元される スパースベクトルsを 求めるもう一つの一般的な方法として、マッチングプシュート(https://en.wikipedia.org/wiki/Matching_pursuit)がある。この方法の本質は、与えられた行列Aの 最初の基底関数a_iが、他の基底関数と比較して最大の係数s_iで入力ベクトルxに フィットするように見つけることである。入力ベクトルからa_i*s_iを 引いた後、得られた残差に次の基底関数を加え、与えられた誤差に達するまで繰り返すのです。マッチング追及法の例として、残差の小さい入力ベクトルに次々と正弦を刻んでいく次のような指標がある。https://www.mql5.com/ru/code/130. 基底関数A(辞書)があらかじめ分かっていない場合、辞書学習と総称される手法で入力データxから 見つけ出す必要がある。 これがスパースコーディング法の最も難しい(そして私にとっては最も興味深い)部分である。前回の講義では、例えば、これらの関数を入力引用符の主ベクトルとするオギの法則によって見つけることができることを紹介した。残念ながら、このような基底関数は、入力データの不連続な記述につながらない(つまり、ベクトルsは 非スパースである)。 不連続な線形変換を導く既存の辞書学習方法は、以下のように分類される。 確率的 クラスター オンライン 基底関数を見つける確率的な 方法は、最大尤度の最大化に還元される。 は、Aに関するP(x|A)を最大化する。 通常、近似誤差はガウス分布を持つと仮定され、以下の最適化問題を解くことになる。 (1), を、(1)基底関数Aを 固定し、ベクトルsに対して()内の式を最小化するステップ、(2)検出ベクトルsを 固定し、基底関数Aに対して 勾配降下法を用いて()内の式を最小化するステップの2段階で解きます。 (2) ここで、上付き文字の(n+1)と(n)は反復回数を表す。この2つのステップ(スパースコーディングステップと辞書学習ステップ)は、ローカルミニマムに達するまで繰り返される。この確率的な基底関数の求め方は、例えば、以下のようなものに用いられている。 オルシュハウゼン、B.A.およびField, D.J.(1996).自然画像に対するスパースコードの学習による単純細胞受容野の特性の創発。Nature, 381(6583), 607-609. Lewicki, M. S., & Sejnowski, T. J. (1999).過完備な表現の学習Neural Comput., 12(2), 337-365. Optimal Directions Method(MOD)は、同じ2つの最適化ステップ(スパースコーディングステップ、辞書学習ステップ)を用いるが、2番目の最適化ステップ(辞書更新ステップ)では、括弧(1)の式のAに関する 微分を0に等化することで基底関数を計算する。 , ここで (3), ここで、s+ は擬似逆行列である。これは、勾配降下法(2)よりも正確な基底行列の計算が可能である。MOD方式については、こちらで詳しく説明しています。 K.エンガン、S.O.アーゼ、そしてJ.H.ハコン=フソイフレーム設計の最適な方向性を示す方法。IEEE International Conference on Acoustics, Speech, and Signal Processing(IEEE国際音響・音声・信号処理会議)Vol.5, pp.2443-2446, 1999. 擬似逆行列の計算は面倒だが、k-SVD法ではそれを避けることができる。 まだ分かっていないのだが。こちらでご紹介しています。 M.アハロン、M.エラド、A.ブラクスタインK-SVD: スパース表現のための過完備な辞書を設計するアルゴリズム.IEEE Trans.信号処理, 54(11), 2006年11月. クラスタリングやオンラインによる辞書の探し方も、まだわかっていません。興味のある読者は、次のアンケートを参照してください。 R.Rubinstein, A. M. Bruckstein, and M. Elad, "Dictionaries for sparse representation modeling,"Proc. of IEEE , 98(6), pp.1045-1057, June 2010. このテーマについて、興味深いビデオ講義をご紹介します。 http://videolectures.net/mlss09us_candes_ocsssrl1m/ http://videolectures.net/mlss09us_sapiro_ldias/ http://videolectures.net/nips09_bach_smm/ http://videolectures.net/icml09_mairal_odlsc/ 以上、今回はこの辺で。今後、機会があれば、また、このフォーラムを訪れた方が興味を持たれるようであれば、このトピックをさらに広げていきたいと思います。 "New Neural" is an Renat Fatkhullin 2011.11.20 00:23 #559 TheXpert: ニコライさん、よく言われることですが、「早すぎる最適化は諸悪の根源」というのがありますよね。使い勝手の悪さをごまかすための開発者の常套句で、いちいち叩かれるほどです。ライフサイクルの長い、高速・高負荷に直結する高品質なソフトウェアの開発について語るならば、この表現は根本的に有害であり、絶対に間違っている。私は、長年のプロジェクト マネジメントの実践の中で、このことを何度も検証してきました。 TheXpert 2011.11.20 00:43 #560 レナート開発者の失態をごまかすための常套句だから、使うたびに叩かれることもある。つまり、いつどんなインターフェースで登場するかわからないような機能を、パフォーマンスを上げるために事前に考慮しなければならないのですね。私は、長年のプロジェクトマネジメントの実践の中で、このことを何度も検証してきました。 では、その長年の経験を活かしてみてはいかがでしょうか。同時に、横柄な口調ではなく、模範となるプロフェッショナリズムを示すことができます。 1...495051525354555657585960616263...100 新しいコメント 取引の機会を逃しています。 無料取引アプリ 8千を超えるシグナルをコピー 金融ニュースで金融マーケットを探索 新規登録 ログイン スペースを含まないラテン文字 このメールにパスワードが送信されます エラーが発生しました Googleでログイン WebサイトポリシーおよびMQL5.COM利用規約に同意します。 新規登録 MQL5.com WebサイトへのログインにCookieの使用を許可します。 ログインするには、ブラウザで必要な設定を有効にしてください。 ログイン/パスワードをお忘れですか? Googleでログイン
そう、それこそが私が知りたかったことなのです。
mql5へ
SZ 現時点での最大の関心事は、データをCPUの特殊な配列にコピーする必要があるのか、通常の関数で配列をパラメータとして渡すことがサポートされるのか、ということです。この問いかけは、プロジェクト全体を根本から変えてしまうかもしれません。
ZZY OpenCLのAPIを提供するだけの計画なのか、それとも独自のラッパーで包む計画なのか、お答えください。
2) ラッパーがあり、HW GPUのみサポートされる(OpenCL 1.1対応)予定。
複数のGPUを選択する場合は、端末の設定によってのみ可能です。
OpenCLは同期的に使用されます。
そう、それこそが私が知りたかったことなのです。
mql5へ
SZ 現時点での最大の関心事は、データをCPUの特殊な配列にコピーする必要があるのか、通常の関数で配列をパラメータとして渡すことがサポートされるのか、ということです。この問いかけは、プロジェクト全体を根本から変えてしまうかもしれません。
ZZZY OpenCLのAPIを提供するだけの予定なのか、それとも独自のラッパーで包む予定なのか、お答えください。
で判断する。
mql5 です。
実際には、サードパーティのDLLをプラグインすることなく、OpenCL.dllのライブラリ関数を直接使用することができます。
OpenCL.dllの関数は、コンパイラが呼び出し自体をリダイレクトしながら、あたかもMQL5のネイティブ関数のように利用できるようになります。
このことから、OpenCL.dllの機能は、現在すでに敷設可能(ダミーコール)であると判断できる。
Renatさん、 mql5 さん、「環境」は正しく理解できましたか?
で判断する。
OpenCL.dllの関数は、あたかもMQL5の ネイティブ関数の ように使うことができ、コンパイラ自身が呼び出しをリダイレクトします。
このことから、OpenCL.dllの機能は、現在すでに敷設可能(ダミーコール)であると判断できる。
Renatさん、 mql5 さん、私の「状況」は合っていますか?
ここまでは、このプロジェクトのスキームです。
オブジェクトは長方形、メソッドは楕円です。処理方法は4つに分類されます。
これら4つのメソッドは、全層にわたる処理全体を記述し、メソッドはメソッドオブジェクトを通じて処理に取り込ま れ、ベースクラスから継承され、ニューロンの種類に応じて必要に応じてオーバーロードされる。
ニコライ 「早すぎる最適化は諸悪の根源」というキャッチフレーズをご存じですね。
OpenCLのことはとりあえず忘れてください。 OpenCLがなくてもまともなことができるようになります。特に、まだ利用できない場合は、必ずトランスポーズする時間があります。
ニコライさん、「早すぎる最適化は諸悪の根源」という言葉がありますよね。
OpenCLのことはとりあえず忘れてください。OpenCLがなくても、まともなものが書けるはずです。いつでも切り替えられる。 それに、まだ内製化された機能はないんだ。
そう、よく言われることで、前回もほぼ同意見だったのですが、分析してみると、ただ企画するだけではGPUのために再設計することはできない、非常に特殊なニーズを持っていることがわかりました。
GPUを使わないのであれば、ニューロン内部の演算と、必要なメモリセルへの演算データの割り当ての両方を担当するNeuronオブジェクトを作り、共通の祖先からクラスを継承することで、必要なニューロンタイプなどを簡単に接続できるようにするのが理にかなっていると思います。
しかし、少し頭を働かせてみると、このやり方ではGPUの計算が完全に崩れ、生まれてくる子どもは這いずり回る運命にあることがすぐにわかったのです。
しかし、上記の私の投稿はあなたを混乱させたと思われます。 そこでの「並列計算法」とは、入力と重みをin*wgで掛け合わせるというかなり具体的な操作のことで、「連続計算法」とは、sum+=a[i]といったような操作のことです。
ただ、将来のGPUとの親和性を考えて、ニューロンから操作を派生させて、レイヤーオブジェクトで1つの動きにまとめ、ニューロンは「どこからどこまでを取るか」という情報のみを提供することを提案します。
講義1はこちらhttps://www.mql5.com/ru/forum/4956/page23
レクチャー2はこちらhttps://www.mql5.com/ru/forum/4956/page34
レクチャー3はこちらhttps://www.mql5.com/ru/forum/4956/page36
レクチャー4はこちらhttps://www.mql5.com/ru/forum/4956/page46
第5講(最終回)。スパース符号化
このテーマが一番面白いので、これから少しずつ書いていこうと思います。だから、時々この記事をチェックするのを忘れないでください。
一般的には、直近のN本の価格提示(ベクトルx)を基底関数(行列Aの 系列)への線形分解として提示することが課題です。
ここで、s は線形変換の係数で、ニューラルネットワークの次の層(例えば SVM)の入力として見つけたいものです。ほとんどの場合、基底関数Aは分かって いる、つまり、あらかじめ選んでいるのである。異なる周波数のサインやコサイン(フーリエ変換)、ガボール関数、Hammotons、ウェーブレット、カーレット、多項式、その他の関数が使用できます。これらの関数があらかじめ分かっている場合、スパースコーディングは、係数sの ほとんどが0になるようなベクトル(スパースベクトル)を求めることになります。ほとんどの情報信号は、信号のサンプル数より少ない数の基底関数で記述される構造を持っているという考え方である。信号のスパース記述に含まれるこれらの基底関数は、信号の分類に必要な特徴である。
元の情報の排出される線形変換を求める問題をCompressed Sensing (http://ru.wikipedia.org/wiki/Compressive_sensing) という。一般に、この問題は次のように定式化される。
sのL0ノルムを最小化する、As = xに従う。
ここで、L0ノルムはベクトルsの 非ゼロ値の数に等しい。この問題を解決する最も一般的な方法は、L0ノルムをL1ノルムに置き換えることであり、これは基底追求法(https://en.wikipedia.org/wiki/Basis_pursuit)の基本である。
のL1ノルムを最小化し、As = x とする。
ここで、L1ノルムは|s_1|+|s_2|+|...+|s_L|として計算される。この問題は、線形最適化に還元される
スパースベクトルsを 求めるもう一つの一般的な方法として、マッチングプシュート(https://en.wikipedia.org/wiki/Matching_pursuit)がある。この方法の本質は、与えられた行列Aの 最初の基底関数a_iが、他の基底関数と比較して最大の係数s_iで入力ベクトルxに フィットするように見つけることである。入力ベクトルからa_i*s_iを 引いた後、得られた残差に次の基底関数を加え、与えられた誤差に達するまで繰り返すのです。マッチング追及法の例として、残差の小さい入力ベクトルに次々と正弦を刻んでいく次のような指標がある。https://www.mql5.com/ru/code/130.
基底関数A(辞書)があらかじめ分かっていない場合、辞書学習と総称される手法で入力データxから 見つけ出す必要がある。 これがスパースコーディング法の最も難しい(そして私にとっては最も興味深い)部分である。前回の講義では、例えば、これらの関数を入力引用符の主ベクトルとするオギの法則によって見つけることができることを紹介した。残念ながら、このような基底関数は、入力データの不連続な記述につながらない(つまり、ベクトルsは 非スパースである)。
不連続な線形変換を導く既存の辞書学習方法は、以下のように分類される。
基底関数を見つける確率的な 方法は、最大尤度の最大化に還元される。
は、Aに関するP(x|A)を最大化する。
通常、近似誤差はガウス分布を持つと仮定され、以下の最適化問題を解くことになる。
(1)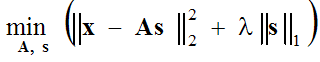 ,
,
を、(1)基底関数Aを 固定し、ベクトルsに対して()内の式を最小化するステップ、(2)検出ベクトルsを 固定し、基底関数Aに対して 勾配降下法を用いて()内の式を最小化するステップの2段階で解きます。
(2)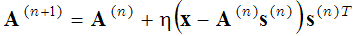
ここで、上付き文字の(n+1)と(n)は反復回数を表す。この2つのステップ(スパースコーディングステップと辞書学習ステップ)は、ローカルミニマムに達するまで繰り返される。この確率的な基底関数の求め方は、例えば、以下のようなものに用いられている。
オルシュハウゼン、B.A.およびField, D.J.(1996).自然画像に対するスパースコードの学習による単純細胞受容野の特性の創発。Nature, 381(6583), 607-609.
Lewicki, M. S., & Sejnowski, T. J. (1999).過完備な表現の学習Neural Comput., 12(2), 337-365.
Optimal Directions Method(MOD)は、同じ2つの最適化ステップ(スパースコーディングステップ、辞書学習ステップ)を用いるが、2番目の最適化ステップ(辞書更新ステップ)では、括弧(1)の式のAに関する 微分を0に等化することで基底関数を計算する。
ここで
(3)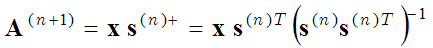 ,
,
ここで、s+ は擬似逆行列である。これは、勾配降下法(2)よりも正確な基底行列の計算が可能である。MOD方式については、こちらで詳しく説明しています。
K.エンガン、S.O.アーゼ、そしてJ.H.ハコン=フソイフレーム設計の最適な方向性を示す方法。IEEE International Conference on Acoustics, Speech, and Signal Processing(IEEE国際音響・音声・信号処理会議)Vol.5, pp.2443-2446, 1999.
擬似逆行列の計算は面倒だが、k-SVD法ではそれを避けることができる。 まだ分かっていないのだが。こちらでご紹介しています。
M.アハロン、M.エラド、A.ブラクスタインK-SVD: スパース表現のための過完備な辞書を設計するアルゴリズム.IEEE Trans.信号処理, 54(11), 2006年11月.
クラスタリングやオンラインによる辞書の探し方も、まだわかっていません。興味のある読者は、次のアンケートを参照してください。
R.Rubinstein, A. M. Bruckstein, and M. Elad, "Dictionaries for sparse representation modeling,"Proc. of IEEE , 98(6), pp.1045-1057, June 2010.
このテーマについて、興味深いビデオ講義をご紹介します。
http://videolectures.net/mlss09us_candes_ocsssrl1m/
http://videolectures.net/mlss09us_sapiro_ldias/
http://videolectures.net/nips09_bach_smm/
http://videolectures.net/icml09_mairal_odlsc/
以上、今回はこの辺で。今後、機会があれば、また、このフォーラムを訪れた方が興味を持たれるようであれば、このトピックをさらに広げていきたいと思います。
ニコライさん、よく言われることですが、「早すぎる最適化は諸悪の根源」というのがありますよね。
使い勝手の悪さをごまかすための開発者の常套句で、いちいち叩かれるほどです。
ライフサイクルの長い、高速・高負荷に直結する高品質なソフトウェアの開発について語るならば、この表現は根本的に有害であり、絶対に間違っている。
私は、長年のプロジェクト マネジメントの実践の中で、このことを何度も検証してきました。
開発者の失態をごまかすための常套句だから、使うたびに叩かれることもある。
つまり、いつどんなインターフェースで登場するかわからないような機能を、パフォーマンスを上げるために事前に考慮しなければならないのですね。
私は、長年のプロジェクトマネジメントの実践の中で、このことを何度も検証してきました。