
チャート分析の良計経済学的アプローチ
事実のない理論は不毛であるが、理論のない事実は無意味である。
K. Boulding
はじめに
よく、マーケットはきまぐれで安しない、ということを耳にします。それで、長期的に成功するトレーディングは不可能だというのです。ですが、それは事実でしょうか?では、これを科学的に分析していきましょう。ここでは計量経済学的 手法を選択し、分析します。なぜそれを選択?まず、MQL コミュニティは精度を重んじます。それは数学と統計がもたらすものです。そして次に、わたしが間違っていなければ、それはこれまで述べられたことがないからです。
本稿だけで、長期的に成功するトレーディングが難しいという問題解決は可能であるということを述べていきます。ただここでは、選択したモデルに対する診断方法を数件だけ述べます。それが将来の利用に値するものであろうことを願って。
また、数式、定理、仮定といったドライな題材を解りやすく述べていくようにしたいと思います。ただし、読者のみなさんが、前提、統計的有意性、統計(統計的基準)、分散、分布、確率、回帰、自己相関といった統計の基本概念は理解しているとした上で進めていきます。
1. 「時系列」の特性
分析の対象 が価格系列(その派生物)、つまり時系列であるのは疑う余地がありません。
計量経済学者は時系列を周波数法(スペクトル分析、ウェーブレット解析)、および時間領域手法(相互相関分析、自己相関分析)の観点から調査します。読者のみなさんはすでに周波数法について述べた『スペクトル分析の構築』 稿はご存じでしょう。ここでは特に、時間領域手法、自己相関分析、条件付き分散に着目していきたいと思います。
非線形モデルは線形モデルよりも価格時系列 についてよく説明します。よって、本稿では非線形モデルに集中的に取り組んでいきます。
価格時系列 には特定の計量経済学モデルによってのみ扱われる特殊な特性があります。まずそういう特性 には『ファットテイル』、予想変動率のクラスタ化、レバレッジ効果が含まれます。
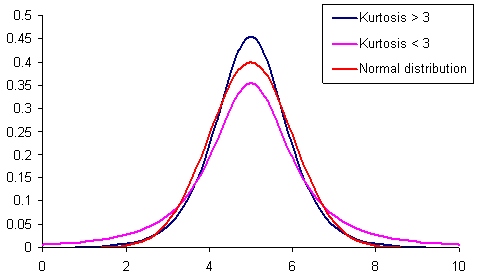
図1 異なるカートシスの分布
図1は異なるカートシス(尖度)の3種類の分布を示しています。通常の尖度より低い分布には他の分布よりもより頻繁に 『ファットテイル』が出現します。それはピンク色で表示されているものです。
われわれが必要とするのは、乱数値の確率密度を表す分布で、これは 調べられた系列の値を数えるのに使います。
予想変動率のクラスタ化(クラスター - 束、密度から)は以下を意味します。高ボラティリティ期間には同じものが続き、低ボラティリティ期間にはそっくり同じものが続きます。昨日価格が変動していたら、おそらく今日も変動するだろうということです。このため、変動の慣性が存在します。図2は変動がクラスタ型を取ることを示しています。
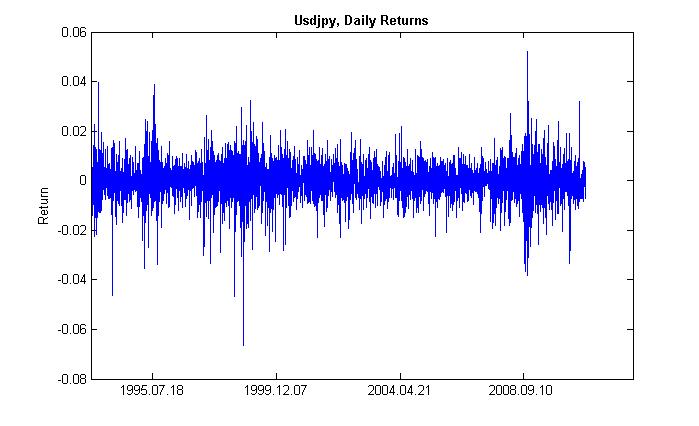
図2 USDJPYの日次戻りの変動はクラスタ化です。
下降マーケットの変動におけるレバレッジ効果は、上昇マーケットのそれよりも高くなります。それはレバレッジ係数の増加によって決定され、株価が落ちるとき、それは借入資産および自己資産の割合に依存します。とはいうものの、この効果は株式市場に適用されるもので、外国為替市場ではありません。この効果についてはこれ以上触れません。
2. GARCHモデル
というわけで、われわれの主要な目標はモデルをいくつか用いて為替レート(価格)を予想することであります。計量経済学者は、量に関して見積もられる一つか二つの効果を示す数学的モデルを使用します。端的に言えば、イベントに対する数式を採用するのです。この方法でそのイベントについて記述します。
分析された時系列が上述のプロパティを備えているとしたら、そのプロパティを草津する最適モデルは非線形モデルです。非線形モデルの中で最も汎用的なものの一つは GARCH モデルです。それはどのように役立つのでしょうか?その本文(関数)内で、系列の変動を考慮します。すなわち、異なる観測期間における分散の変動性です。計量経済学者はこの効果を難解な用語 - 不均一分散 (ギリシャ語のヘテロ:異なる+スケダーシス:分散からきています。)
式そのものを見ると、このモデルが現在の分散変動性 (σ2t) 以前のパラメータ変更 (ϵ2t-i) と前回の分散推定(いわゆる『オールドニュース』と呼ばれるもの)(σ2t-i)双方の影響を受けていることを示しているのが判ります。
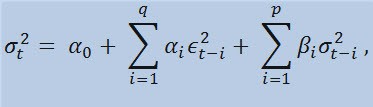
限度を設け
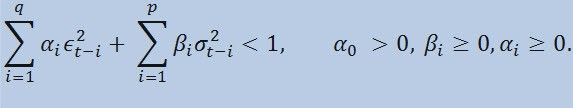
ここで、 ϵt - 非正規イノベーション; α0 , βi , αi , q (ARCH メンバ ϵ2の順序)、 p(GARCH メンバ σ2の順序) - 推定されたパラメータとモデル順序
3. 戻りのインディケータ
実際、ここでは価格系列自体ではなく、リターン系列 の推定を行います。価格変動(絶えずチャージされるリターン)の対数は、リターンのパーセンテージの自然対数として決定されます。
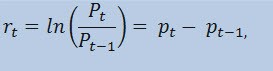
ここで
- Pt - 時刻 t ;における価格系列の値
- Pt-1 - 時刻 t-1; における価格系列の値
- pt = ln(Pt) - 自然対数Pt
価格よりもリターンで作業をする方が好ましい主な理由は、リターンは統計的に価格よりも優れた特性を持つことです。
リターンのインディケータ ReturnsIndicator.mq5を作成します。ここではたいへん有用なものです。ここで、インディケータ作成のアルゴリズムを解りやすく解説している『初心者のためのカスタムインディケータ』 稿を参照していきます。お話した式が導入される箇所でコードだけを表記しているのはこのためです。とても簡単なので説明は不要だと思います。
//+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, // size of the array price[] const int prev_calculated, // number of bars available at the previous call const int begin, // index of the array price[] the reliable data starts from const double& price[]) // array for the calculation itself { //--- int start; if(prev_calculated<2) start=1; // start filling ReturnsBuffer[] from the 1-st index, not 0. else start=prev_calculated-1; // set 'start' equal to the last index in the arrays for(int i=start;i<rates_total;i++) { ReturnsBuffer[i]=MathLog(price[i]/price[i-1]); } //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
ひとつお伝えしておきたいのは、リターン系列は常に一番目の系列より1エレメント小さいということです。それが、二番目のエレメントから始めてリターン系列を計算する理由です。最初のエレメントは必ず0です。
ReturnsIndicator インディケータを使用し、この調査対象とする無作為な時系列を取得します。
4. 統計的検定
統計的検定の番がやってきました。統計的検定はあるモデル、または別のモデルを使用する適切性を確認する兆候が時系列に見られるか判断するために行います。ここではそのモデルというのはGARCH モデルです。
Q-test of Ljung-Box-Pierceを使い、系列の 自己相関 が無作為か関連があるか確認します。このために、新しい関数を書く必要があります。ここで自己相関 t1 および t2 という時刻における同じ時系列X (t) の値間の相関関係(確率的関連)を意味します。t1 および t2 という時刻が隣接していたら(それぞれが前後していたら)、系列メンバと1時間単位で移動した同系列のメンバ: x1, x2, x3, ... и x1+1, x2+1, x3+1, ...間の関係を調査します。移動されたメンバーの結果をラグ (待ち時間、遅延)と呼びます。ラグはどのような数字も値として取ることができます。
括弧コメントを書き、以下の点をお話します。私が知る限り С++ 言語も MQL5 言語も複雑で平均的な統計的計算をする標準ライブラリは内蔵していません。通常、そういった計算は特殊な統計データ処理ツールを使用して行います。私としては、この問題に対応するのに Matlab、STATISTICA 9などのツールを使用するのが簡単かと思います。ただ、外部ライブラリの使用は避けることにしました。まずMQL5 言語が計算に強いことをお見せするためです。そしてMQL コードを書くうちに自分で多くのことを学びました。
ここで次のコメントを作成する必要があります。Q 検定を作成するのには複雑な複素数が必要です。というわけでComplex クラスを作成しました。CComplexと呼ぶのがふさわしいでしょう。ここで少しリラックスしたいと思います。読者のみなさんはご存じでしょうから、複素数 がなんたるか説明は不要でしょう。個人的には、MQL5 および MQL4に公開されているフーリエ変換を計算する関数は好みません。そこでは間接的な方法で複素数が使用されているからです。その上、もうひとつ別の障害もあります。MQL5言語では、算術的処理をオーバーライドできないのです。ゆえに、ここでは別の方法を探し、標準的 'C' 言語表記は避ける必要がありました。そこで、以下の方法で複素数のクラスを実装しました。
class Complex { public: double re,im; //re -real component of the complex number, im - imaginary public: void Complex(){}; //default constructor void setComplex(double rE,double iM){re=rE; im=iM;}; //set method (1-st variant) void setComplex(double rE){re=rE; im=0;}; //set method (2-nd variant) void ~Complex(){}; //destructor void opEqual(const Complex &y){re=y.re;im=y.im;}; //operator= void opPlus(const Complex &x,const Complex &y); //operator+ void opPlusEq(const Complex &y); //operator+= void opMinus(const Complex &x,const Complex &y); //operator- void opMult(const Complex &x,const Complex &y); //operator* void opMultEq(const Complex &y); //operator*= (1-st variant) void opMultEq(const double y); //operator*= (2-nd variant) void conjugate(const Complex &y); //conjugation of complex numbers double norm(); //normalization };
たとえば、2つの複素数を合計する処理はメソッド opPlus, を、減算はメソッド opMinusを用いて行うなどです。コード c = a + b (ここで a, b, с は複素数)を書く場合、コンパイラはエラーを表示します。が、次の式は受け付けます。c.opPlus(a,b)
必要があれば、ユーザーは Complex クラスのメソッドセットを拡張することが可能です。例として、除算のオペレータを追加することができます。
また、複素数配列を処理する予備関数も必要です。配列エレメントの処理をComplex クラスのループ内ではなく外に実装つつ参照渡しされる配列を直接動作するようにしたのはそのためです。合計3個がそのような関数です。
- getComplexArr (複素数配列から二次元実数配列を返します。)
- setComplexArr getComplexArr (一次元実数配列複から複素数配列を返します。)
- setComplexArr2 setComplexArr getComplexArr (二次元実数配列複から複素数配列を返します。)
こういった関数は参照によって渡される配列を返すことに注意が必要です。そのため、これら関数本文には「戻り」オペレータが含まれていません。しかし論理的に考えると、ボイドタイプではなくリターンタイプを取り上げるのがよいでしょう。
複素数クラスおよび予備関数については、ヘッダファイル Complex_class.mqhで述べられています。
そして、検定を作成するにあたり、自己相関関数と フーリエ変換関数が必要です。そこで新しいクラスを作成し、 CFFTと名づけます。それは、フーリエ変換のための複素数配列処理を行います。フーリエクラスは以下のようなものです。
class CFFT { public: Complex Input[]; //input array of complex numbers Complex Output[]; //output array of complex numbers public: bool Forward(const uint N); //direct Fourier transformation bool InverseT(const uint N,const bool Scale=true); //weighted reverse Fourier transformation bool InverseF(const uint N,const bool Scale=false); //non-weighted reverse Fourier transformation void setCFFT(Complex &data1[],Complex &data2[],const uint N); //set method(1-st variant) void setCFFT(Complex &data1[],Complex &data2[]); //set method (2-nd variant) protected: void Rearrange(const uint N); // regrouping void Perform(const uint N,const bool Inverse); // implementation of transformation void Scale(const uint N); // weighting };
フーリエ変換はすべて配列によって行われ、その長さは条件 2^N(2のN乗)の条件に従う、ということに注意が必要です。通常は配列の長さは 2^Nではありません。この場合、2^N >= n(nは配列の長さ)について配列の長さは2^Nまで増えます。配列の追加エレメントは 0です。このような配列処理はautocorr 関数本文内で予備関数 nextpow2とpowを用いて行われます。
int nFFT=pow(2,nextpow2(ArraySize(res))+1); //power rate of two
よって、長さ(n) が73585の初期配列があるとすると、 nextpow2 関数が値 17を返します。ここで2^17 = 131072です。別の言い方をすると、戻り値は pow(2, ceil(log(n)/log(2)))分n より大きいのです。そして、値nFFT: 2^(17+1) = 262144を計算します。これは予備配列の長さとなり、73585 ~ 262143のそのエレメントははゼロとなります。
フーリエクラスについては、ヘッダファイルFFT_class.mqhに記載があります。
誌面の節約のため、CFFT クラスの実装については述べません。ご興味がおありの方は、添付のインクルードファイルで確認できます。では、自己相関関数に進みます。
void autocorr(double &ACF[],double &res[],int nLags) //1-st variant of function /* selective autocorrelation function (ACF) for unidimensional stochastic time series ACF - output array of calculated values of the autocorrelation function; res - array of observation of stochastic time series; nLags - maximum number of lags the ACF is calculated for. */ { Complex Data1[],Data21[], //input arrays of complex numbers Data2[],Data22[], //output arrays of complex numbers cData[]; //array of conjugated complex numbers double rA[][2]; //auxiliary two-dimensional array of real numbers int nFFT=pow(2,nextpow2(ArraySize(res))+1); //power rate of two ArrayResize(rA,nFFT);ArrayResize(Data1,nFFT); //correction of array sizes ArrayResize(Data2,nFFT);ArrayResize(Data21,nFFT); ArrayResize(Data22,nFFT);ArrayResize(cData,nFFT); double rets1[]; //an auxiliary array for observing the series double m=mean(res); //arithmetical mean of the array res ArrayResize(rets1,nFFT); //correction of array size for(int t=0;t<ArraySize(res);t++) //copy the initial array of observation // to the auxiliary one with correction by average rets1[t]=res[t]-m; setComplexArr(Data1,rets1); //set input array of complex numbers CFFT F,F1; //initialize instances of the CFFT class F.setCFFT(Data1,Data2); //initialize data-members for the instance F F.Forward(nFFT); //perform direct Fourier transformation for(int i=0;i<nFFT;i++) { Data21[i].opEqual(F.Output[i]);//assign the values of the F.Output array to the Data21 array; cData[i].conjugate(Data21[i]); //perform conjugation for the array Data21 Data21[i].opMultEq(cData[i]); //multiplication of the complex number by the one adjacent to it //results in a complex number that has only real component not equal to zero } F1.setCFFT(Data21,Data22); //initialize data-members for the instance F1 F1.InverseT(nFFT); //perform weighter reverse Fourier transformation getComplexArr(rA,F1.Output); //get the result in double format after //weighted reverse Fourier transformation for(int i=0;i<nLags+1;i++) { ACF[i]=rA[i][0]; //in the output ACF array save the calculated values //of autocorrelation function ACF[i]=ACF[i]/rA[0][0]; //normalization relatively to the first element } }
これで、ラグの指定数に対して ACF 値を計算しました。Q 検定に自己相関関数の使用が可能です。検定関数自体は以下のようなものです。
void lbqtest(bool &H[],double &rets[]) /* Function that implements the Q test of Ljung-Box-Pierce H - output array of logic values, that confirm or disprove the zero hypothesis on the specified lag; rets - array of observations of the stochastic time series; */ { double lags[3]={10.0,15.0,20.0}; //specified lags int maxLags=20; //maximum number of lags double ACF[]; ArrayResize(ACF,21); //epmty ACF array double acf[]; ArrayResize(acf,20); //alternate ACF array autocorr(ACF,rets,maxLags); //calculated ACF array for(int i=0;i<20;i++) acf[i]=ACF[i+1]; //remove the first element - one, fill //alternate array double alpha[3]={0.05,0.05,0.05}; //array of levels of significance of the test /*Calculation of array of Q statistics for selected lags according to the formula: L |----| \ Q = T(T+2) || (rho(k)^2/(T-k)), / |----| k=1 where: T is range, L is the number of lags, rho(k) is the value of ACF at the k-th lag. */ double idx[]; ArrayResize(idx,maxLags); //auxiliary array of indexes int len=ArraySize(rets); //length of the array of observations int arrLags[];ArrayResize(arrLags,maxLags); //auxiliary array of lags double stat[]; ArrayResize(stat,maxLags); //array of Q statistics double sum[]; ArrayResize(sum,maxLags); //auxiliary array po sums double iACF[];ArrayResize(iACF,maxLags); //auxiliary ACF array for(int i=0;i<maxLags;i++) { //fill: arrLags[i]=i+1; //auxiliary array of lags idx[i]=len-arrLags[i]; //auxiliary array of indexes iACF[i]=pow(acf[i],2)/idx[i]; //auxiliary ACF array } cumsum(sum,iACF); //sum the auxiliary ACF array //by progressive total for(int i=0;i<maxLags;i++) stat[i]=sum[i]*len*(len+2); //fill the array Q statistics double stat1[]; //alternate of the array of Q statistics ArrayResize(stat1,ArraySize(lags)); for(int i=0;i<ArraySize(lags);i++) stat1[i]=stat[lags[i]-1]; //fill the alternate array of specified lags double pValue[ArraySize(lags)]; //array of 'p' values for(int i=0;i<ArraySize(lags);i++) { pValue[i]=1-gammp(lags[i]/2,stat1[i]/2); //calculation of 'p' values H[i]=alpha[i]>=pValue[i]; //estimation of zero hypothesis } }
関数は Ljung-Box-PierceのQ検定 を処理し、指定のラグに対し理論値の配列を返します。Ljung-Box の検定はいわゆる 混成検定 (結合テスト)であることを明確にする必要があります。それは、指定のラグまでラグのグループはいくつか自己相関の存在について確認されるということを意味します。通常、自己相関はラグ全体の10番目、15番目、20番目まで確認されます。全系列にての自己相関の有無についての結論は、H 配列のエレメントの最終値を基に作成されます。すなわち1番目~ 20番目のラグです。
配列エレメントがfalseの場合、ゼロ仮説は却下されません。それは前回および選択されたラグに自己相関は認められないとコメントします。別の言い方をすると、値が falseの場合は、自己相関がないということです。それ以外、検定は自己相関の存在を証明します。ゼロ仮説の代替は値が trueのとき受け付けられます。
ときとして、リターン系列に自己相関が認められないこともあります。この場合、信頼性を高めるため、リターンの二乗が検証されます。最終的にゼロ仮説を受け入れるか却下するかの判断はリターンの一番目の系列検定同様の方法で行います。リターンに二乗を使う理由はなんでしょうか?この方法で、分析する系列で起こりうるノンランダムな自己相関コンポーネントを人為的に増やします。それは信頼される限界の初期値範囲内でさらに判断されるものです。理論的にはリターンの二乗その他乗数を使用することが可能です。ただそれは不要な統計的負荷で、それでは検定の意味がなくなります。
値'p' が計算されるとき、Q 検定本文の末尾に関数 gammp(x1/2,x2/2) があります。それにより、対応するエレメントに対して不完全なガンマ関数を計算することができます。実は、χ2 分布 (カイ二乗分布)の累積関数が必要なのです。しかし、それはガンマ分布の特殊なケースです。
一般的には、GARCH モデル使用の安定性を証明するのには Q 検定の任意ラグの正の値を取得するだけで十分です。また、計量経済学者はもうひとつ別の検定を行います。それはエングルのARCH検定で、それにより従来型の不均一分散の有無を確認します。ただ、いまは Q 検定で十分だと思います。それが最も汎用的なものだからです。
検定を行うにあたり必要な関数はそろいました。ここから得られた結果の画面表示について考えていく必要があります。このためにメッセージウィンドウおよび自己相関図形式で計量経済学検定の結果を表示する関数lbqtestInfo を書きました。自己相関図は分析したシンボルのチャートの右に表示されます。
例を使って結果を見てみます。. 最初に分析するシンボルとしてusdjpy を選択しました。まず、シンボル(終値)の棒グラフを開き、カスタムインディケータ ReturnsIndicator をロードしてリターン系列を表示します。チャートはインディケータのボラティリティクラスタをきれいに表示するため最大限縮小します。そして、スクリプトGarchTestを実行します。 おそらくみなさんの画面解像度は私のと違っているでしょうから、スクリプトがお望みのピクセル表示のダイアグラムサイズを尋ねてきます。私の標準サイズは700*250です。
図3に複数の検定例を示しています。
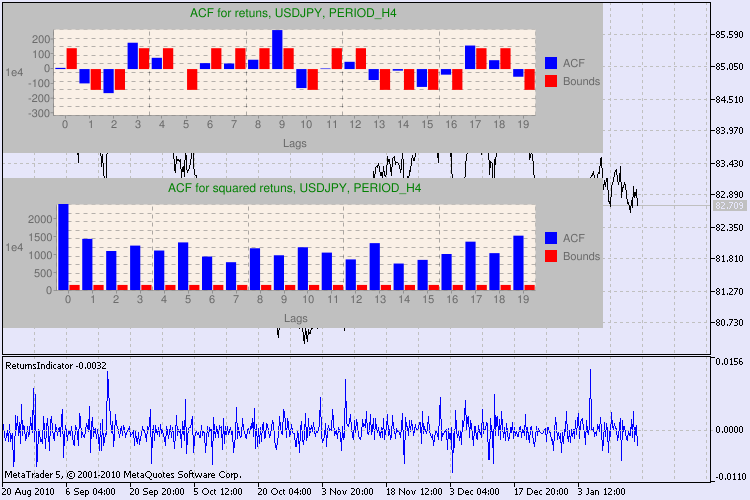
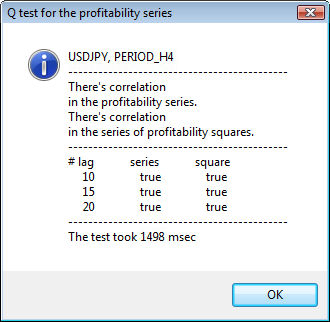
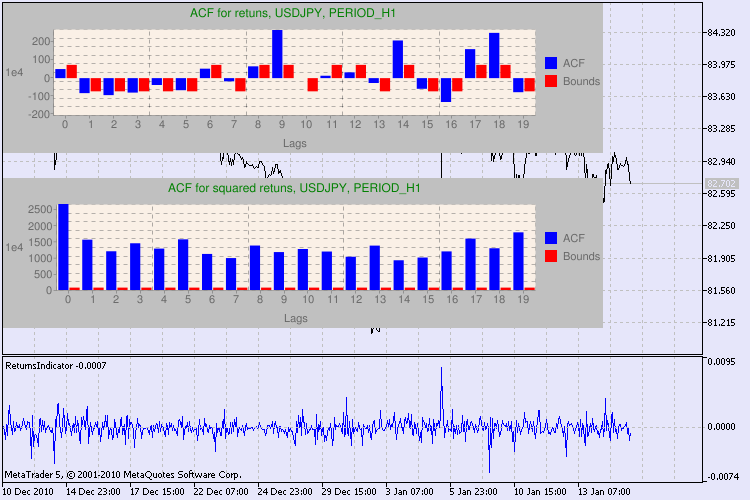
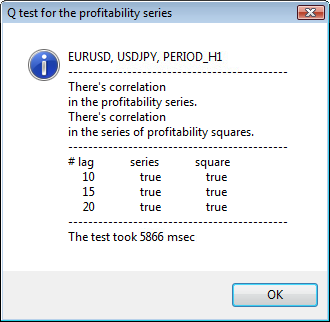
図3 Q 検定結果と 異なる時間枠でのUSDJPYに対する自己相関ダイアグラム
MetaTrader 5でシンボルチャートについて異なるダイアグラム表示をさがしました。そして、別の方法として最適なのはGoogle Chart APIを用いた図描画ライブラリを使用することだと判断しましたGoogle Chart APIに関しては、それを取り上げた記事に記載があります。
この情報をどう読み解いていくのでしょうか?それでは結果表示を見ていきます。チャートの上部には リターンの初期系列に対する自己相関関数(ACF)があります。最初のグラフではH4時間枠の usdjpy 系列を分析します。値ACF (ブルーのバー)が複数個限界(赤色バー)を越えているのが判ります。すなわち、リターンの最初の系列には小規模な自己相関が認められます。下の図は指定シンボルのリターンの二乗の系列の自己相関関数 (ACF) グラフです。すべてが明白で、ブルーバーの完全勝利です。H1 図も同様に分析されます。
グラフの軸について少々お話します。x 軸については問題ないでしょう。ラグの指数を表示しています。y 軸には、指数値が確認できます。ACF の初期値がかけ算されています。よって1e4 は初期値が 1e4 (1e4=10000)倍されていることを意味し、1e2 は100でかけ算されていることを意味します、などです。このようなかけ算はグラフを読みやすくしようというものです。
ダイアログウィンドウの上側には、シンボルまたはクロスペア名と時間枠が表示されています。その後には、リターンの初期系列およびリターンの二乗系列内での自己相関の有無に関する2文が確認できます。10番目、15番目、20番目のタグはリターンの初期系列値およびリターンの二乗系列値と共に挙げられています。ここには自己相関の相対値が表示されます。 - 前回および指定のフラグに自己相関があるかどうか判断する Q検定中のブーレアンフラグです。
そして、前回および指定のフラグに自己相関がある場合、フラグはtrue、それ以外は falseです。最初のケースでは、われわれの系列は非線形 GARCH モデルに適用する『クライアント』で、二番目のケースではシンプルな分析モデルが必要です。注意深い読者の方はお気づきでしょうが、 USDJPY ペアのリターンの初期系列はやや相互相関しています。特に大きな時間枠でそれが認められます。ただ、リターンの二乗系列は自己相関を示しています。
検定時間はウィンドウの下部に表示されています。
検定全体はGarchTest.mq5 スクリプトを使用して行われました。
おわりに
本稿では、計量経済学者がどのように時系列を分析するか、もっと正確にどのように計量経済学者が研究を開始するか述べてきました。その間、多くの関数や複数タイプのデータ(複素数など)のコードを書く必要がありました。おそらく、初期系列の目測でも計量経済学的推定と同様の結果を得られることでしょう。ただ、精巧な方法の使用ということでしたから今回の手法を用いました。優秀な医師は複雑な技術や方法論を使わなくても診断が下せるものです。患者を注意深く慎重に観察するのです。
何が本稿で述べられた方法から得られるのでしょうか?非線形GARCHモデルの使用により、正式に数学的観点から分析した系列を表現することが可能で、指定したステップ数に対して予想をすることができます。 その上、予想期間の系列の動きをシミュレーションし、予測情報を使用して既製のExpert Advisorを検証することにも役立ちます。
ファイル格納場所:
| # | ファイル | パス |
|---|---|---|
| 1 | ReturnsIndicator.mq5 | %MetaTrader%\MQL5\Indicators |
| 2 | Complex_class.mqh | %MetaTrader%\MQL5\Include |
| 3 | FFT_class.mqh | %MetaTrader%\MQL5\Include |
| 4 | GarchTest.mq5 | %MetaTrader%\MQL5\Scripts |
ファイルおよびライブラリ記述 google_charts.mqh また Libraries.rar は 前述の記事よりダウンロード可能です。
参照文献
- Analysis of Financial Time Series, Ruey S. Tsay, 2nd Edition, 2005. - 638 pp.
- Applied Econometric Time Series,Walter Enders, John Wiley & Sons, 2nd Edition, 1994. - 448 pp.
- Bollerslev, T., R. F. Engle, and D. B. Nelson. "ARCH Models." Handbook of Econometrics. Vol. 4, Chapter 49, Amsterdam: Elsevier Science B.V.
- Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Upper Saddle River, NJ: Prentice-Hall, 1994.
- Numerical Recipes in C, The Art of Scientific Computing, 2nd Edition, W.H. Press, B.P. Flannery, S. A. Teukolsky, W. T. Vetterling, 1993. - 1020 pp.
- Gene H. Golub, Charles F. Van Loan. Matrix computations, 1999.
- Porshnev S. V. "Computing mathematics. Series of lectures", S.Pb, 2004.
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/222
 MT4ビルド600以降のバージョンのデータ構造と保存場所
MT4ビルド600以降のバージョンのデータ構造と保存場所
 ミクロ、ミドル、メイントレンドのインディケータ
ミクロ、ミドル、メイントレンドのインディケータ
 新しいMetaTrader 4ビルド600以降へのアップデート
新しいMetaTrader 4ビルド600以降へのアップデート
 トレーディングモデルに基づくマルチエキスパートアドバイザーの作成
トレーディングモデルに基づくマルチエキスパートアドバイザーの作成
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索