MQL5の圏論（第18回）：ナチュラリティスクエア（自然性の四角形）

はじめに

MQL5におけるトレーダーにとっての圏論の位置づけは主観的なものになるに違いありません。本連載ではこれまで、金融データの予測や分類を行うために、オブジェクト上の射を重視するシステム全体のアプローチを用いてきました。

自然変換は、圏論における重要な概念であり、単に関手間の写像と見なされることが多いです。関手が2つのオブジェクトをリンクしていると考えると、この平凡な見方は、間違ってはいないものの、混乱を招く可能性があります。なぜなら、問題はどのオブジェクトが自然変換をリンクするのかということだからです。簡単な答えは、関手の2つの終域オブジェクトです。この記事では、この定義に至る構築物を示し、また、ボラティリティの変化を予測するためにこの射を使用するエキスパートトレーリングクラスのインスタンスを含めることにします。

自然変換を説明する例として使用する圏は2つです。これは自然変換を定義するために使用する関手の対の最小数です。1つ目は、正規化された指標値からなる2つのオブジェクトで構成されます。ここで検討する指標は、ATRとボリンジャーバンドの値です。2つ目の圏は、2つの関手が終域圏につながるので、終域圏として機能します。これには、予測したい値の価格帯を取得する4つのオブジェクトが含まれます。

圏について

指標値の圏については、ここで説明する概念の理解を助けるためにのみ、この記事で触れています。結局のところ、私たちが直面しているボラティリティを予測する上で、それは最小限の役割しか果たしていません。

添付ファイルに関する注意事項

SignalCT_16_.mqhをMQL5\include\Expert\Signal\フォルダに配置して、ct_16.mqhをMQL5\include\フォルダに配置してください。

さらに、エキスパートアドバイザー(EA)の一部としてそれらを組み立てる必要があるため、ウィザードを使用してEAを組み立てる方法についてこちらのガイドに従ってください。記事にあるように、トレーリングストップなしで、固定証拠金を資金管理に使いました。どちらもMQL5のライブラリの一部です。いつものように、この記事の目的は、聖杯を紹介することではなく、読者自身の戦略にカスタマイズできるアイデアを紹介することです。

には、これを達成するために主にナチュラリティスクエアに頼ることになるからです。しかし、それは基礎的なものです。ナチュラリティスクエアに関する決定的な情報はネット上にはあまりないですが、この投稿は、ここで紹介されている以外の情報を探している人にとっては興味深い読み物でしょう。

始域圏に戻ると、前述のように2つのオブジェクトがあり、1つはATRの値、もう1つはボリンジャーバンドの値です。これらの値は、オブジェクトが一定のカーディナリティ（サイズ）を持つように正規化されます。各オブジェクトで表される値は、それぞれの指標値の変化です。これらの変更は、マイナス100%からプラス100%まで10%のステップで記録されます。。これは、各オブジェクトのカーディナリティが21であることを意味します。そのため、以下の値で構成されています。

{

-100, -90, -80, -70, -60, -50, -40, -30, -20, -10,

 0,

 10, 20, 30, 40, 50, 60, 70, 80, 90, 100

}

これらの要素同一のオブジェクトをリンクする射は、それらが同時に登録されたかどうかに基づいて値をペアリングし、2つの指標値の変化の現在のログを提供します。

これらの指標変化値は、他のボラティリティ関連指標のものでも可能です。原則は変わりません。指標値の変化を、前と現在の指標の値の絶対値の合計で割って、小数を得ます。この小数を10倍して、小数点以下は四捨五入されます。次に、この値に再び10を乗じ、それが等価であるかどうかに応じて、上記のオブジェクトのインデックスを割り当てます。

価格帯の圏は、プロジェクションをおこなう際に使用するナチュラリティスクエアのメインとなる4つのオブジェクトで構成されます。始域圏（指標の変更を伴う）は2つのオブジェクトから構成され、そこからこの終域につながる2つの関手があるので、これらの関手のそれぞれがオブジェクトに写像されていることになります。写像されるオブジェクトは常に別々である必要はありませんが、今回のケースでは概念を明確にするために、始域圏に写像される各オブジェクトに、価格帯圏にある独自の終域オブジェクトを持たせています。このように、2つのオブジェクトに2つの関手を乗じると、4つの終域オブジェクトが得られます。

4つのオブジェクトがあり、重複を避けたいので、各オブジェクトで異なる価格帯の変更を記録します。これを支援するために、2つの関手は異なる予測デルタを表します。一方の関手は1本後の価格帯を写像し、もう一方の関手は2本後の価格帯の変化を写像します。加えて、ATRオブジェクトからの写像は、1本のバーにわたる価格範囲に対応するものであるのに対し、ボリンジャーバンドオブジェクトからの写像は、2本のバーにわたる価格範囲に対応するものです。これは、これを実装する以下のコードで要約できます。

      CElement<string> _e;
      for(int i=0;i<m_extra_training+1;i++)
      {
         double _a=((m_high.GetData(i+_x)-m_low.GetData(i+_x))-(m_high.GetData(i+_x+1)-m_low.GetData(i+_x+1)))/((m_high.GetData(i+_x)-m_low.GetData(i+_x))+(m_high.GetData(i+_x+1)-m_low.GetData(i+_x+1)));
         double _c=((m_high.GetData(i+_x)-m_low.GetData(i+_x))-(m_high.GetData(i+_x+2)-m_low.GetData(i+_x+2)))/((m_high.GetData(i+_x)-m_low.GetData(i+_x))+(m_high.GetData(i+_x+2)-m_low.GetData(i+_x+2)));
         double _b=((fmax(m_high.GetData(i+_x),m_high.GetData(i+_x+1))-fmin(m_low.GetData(i+_x),m_low.GetData(i+_x+1)))
                     -(fmax(m_high.GetData(i+_x+2),m_high.GetData(i+_x+3))-fmin(m_low.GetData(i+_x+2),m_low.GetData(i+_x+3))))
                     /((fmax(m_high.GetData(i+_x),m_high.GetData(i+_x+1))-fmin(m_low.GetData(i+_x),m_low.GetData(i+_x+1)))
                     +(fmax(m_high.GetData(i+_x+2),m_high.GetData(i+_x+3))-fmin(m_low.GetData(i+_x+2),m_low.GetData(i+_x+3))));
         double _d=((fmax(m_high.GetData(i+_x),m_high.GetData(i+_x+1))-fmin(m_low.GetData(i+_x),m_low.GetData(i+_x+1)))
                     -(fmax(m_high.GetData(i+_x+3),m_high.GetData(i+_x+4))-fmin(m_low.GetData(i+_x+3),m_low.GetData(i+_x+4))))
                     /((fmax(m_high.GetData(i+_x),m_high.GetData(i+_x+1))-fmin(m_low.GetData(i+_x),m_low.GetData(i+_x+1)))
                     +(fmax(m_high.GetData(i+_x+3),m_high.GetData(i+_x+4))-fmin(m_low.GetData(i+_x+3),m_low.GetData(i+_x+4))));
         
         ...
      }

これらのオブジェクトは、現在の変更のみを記録するため、単一サイズとなります。それらの間の射は、単一バーの価格帯の予測から2つの価格バーの先の2つのバーの価格帯の予測まで正方形の可換図式で流れます。これについては、以下で自然変換を正式に定義する際に詳しく説明します。

価格帯とソースとなった市場データとの関係は、上記のソースにも示されています。各オブジェクトに記録された変化は、指標値のように正規化されるのではなく、範囲の変化を現在と以前の価格帯の合計で割って、丸めなしの10進数値を生成します。

関手：指標値と価格帯のリンク

関手は4回にわたって紹介しましたが、ここでは2つの圏の対として取り上げます。関手はオブジェクトだけを写像するのではなく、射も写像することを思い出してください。指標値の始域圏には2つのオブジェクトと1つの射があるので、各関手に対してオブジェクトから2つ、射から1つ、合計3つの出力点が終域圏に存在することになります。関手が2つあれば、終域はの端点は6つになります。

正規化された指標の整数値を10進数の価格帯の変化（生の値ではなく端数として記録される変化）に写像することは、過去2回の記事で検討したように、多層パーセプトロンの助けを借りて達成することができます。例えば、ランダムフォレストなど、本連載ではまだ未踏の写像の方法が他にもたくさんあります。

この図解は、あくまでも念のためです。自然変換とは何か、その前提条件をすべて正しく示すためのものです。トレーダーとして新しい概念に直面したとき、常に重要なのは、その応用と利益は何かということです。冒頭で、今回の予想では終域圏の4つのオブジェクトによってのみ決定されるナチュラリティスクエアが焦点になると述べたのは、このためです。つまり、ここで始域圏とそのオブジェクトについて言及したのは、単に自然変換を定義するのに役立つから、この記事のための特定の応用に役立つからではありません。

自然変換：ギャップを埋める

これが明確になったので、次に自然変換の公理を見て、応用に移ることができます。正式には、関手間の自然な変換

F:C-->D

および

G:C-->D

は、圏CのすべてのオブジェクトAに対しての、射

ηA：F(A) -->G(A)

のファミリーで、圏Cでのすべての射

f:A-->B

について、次の図を可換にするものです。

 

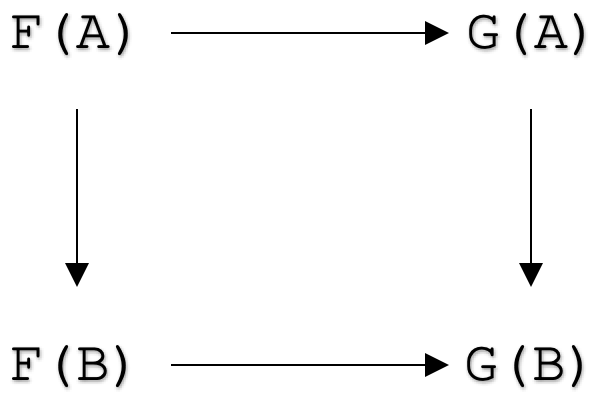
自然変換に関する資料はネット上にいくらでもありますが、それにもまして、ナチュラリティスクエアに至るまでの定義をより分かりやすく説明したものを見ることは有益でしょう。そのために、2つの圏CとDがあり、圏Cには次のように定義された2つのオブジェクトXとYがあるとします。

X = {5, 6, 7}

および

Y = {Q, R, S}

。また、これらのオブジェクトの間に、f(5)=S、f(6)=R、f(7)=Rとなるような、次のように定義される射fがあるとします。

f:X→Y

。

この例では、圏CとDの間の2つの関手FとGが、2つの単純なことをします。リストとリストのリストをそれぞれ用意します。つまり、関手FをXに適用すると、次が出力されます。

[5, 6, 5, 7, 5, 6, 7, 7]

同様に、関手G（リストのリスト）では次が出力されます。

[[5, 6], [5, 7, 5, 6, 7], [7]]

これらの関手をオブジェクトYに同様に適用すると、終域圏Dに4つのオブジェクトができることになります。これらは以下のように表されます。

始域圏Cには2つのオブジェクトがあるので、Cのオブジェクトに対してそれぞれ2つの自然変換を行うことになります。これらは以下のように表されます。

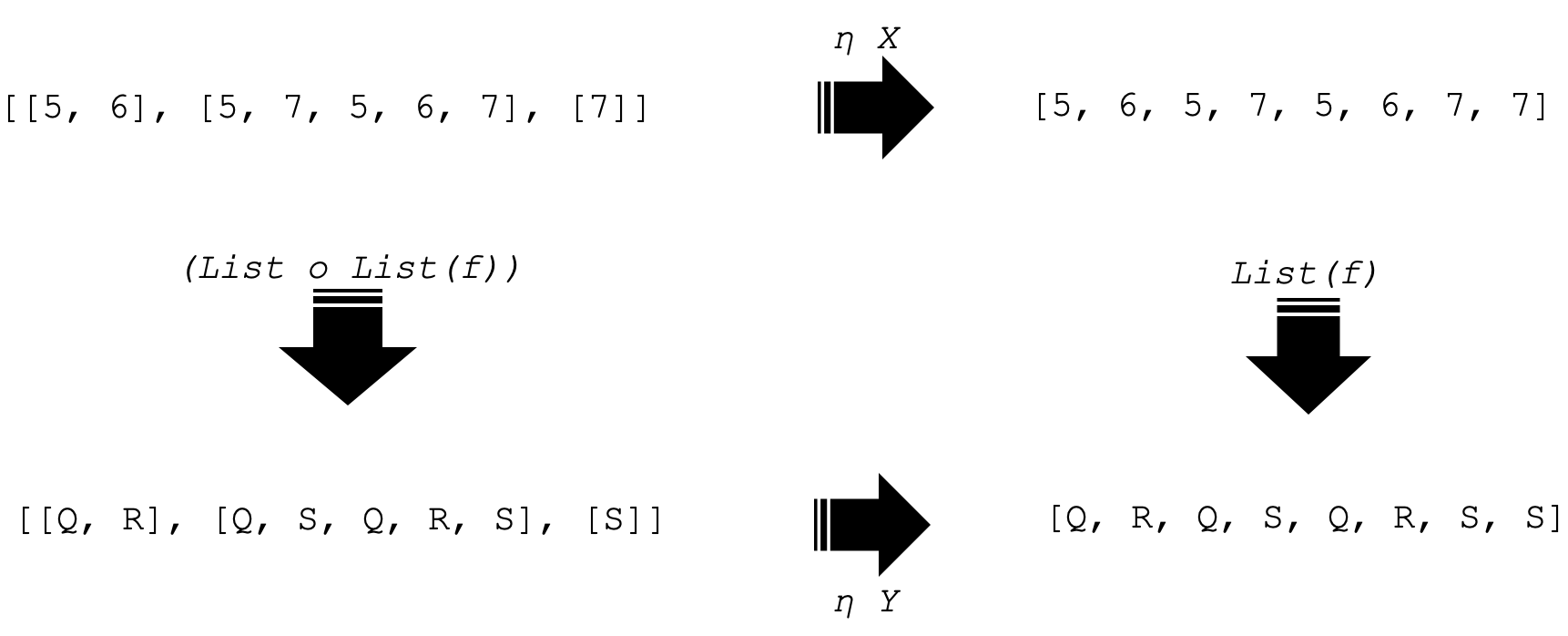
上記の表現は自然性の二乗です。そして、矢印が示すように可換です。つまり、2つの横の矢印は、Cの各オブジェクトに関する私たちの自然変換(NT)であり、縦の矢印は、関手FとGに対して圏Cの射fに適用したときの関手出力です。

構造と関係を維持することの重要性は、見過ごされがちなNTの重要な側面です。しかし、これは非常に単純ではありますが、非常に重要です。主張を明確にするために、料理の分野の例を考えてみましょう。2人の有名なシェフ（AとB）が、それぞれ標準的な食材から同じ料理を作る独自な方法を持っているとします。食材は、食材の種類というより広い圏に属するオブジェクトであり、各シェフが作る2つの料理は、料理の種類というまた別のより広い圏に属すると考えます。シェフAとシェフBが作る2つの料理の間の自然変換は、シェフAが作る料理をシェフBが作る料理に変更するために必要な材料、余分な調理準備を記録することになります。このアプローチでは、より多くの情報を記録し、実際に、例えばシェフCの料理がシェフBの料理と一致するために同様のNTを必要とするかどうか、またはそうでない場合はどの程度かをチェックし、確認することができます。しかし、NTがBシェフの料理を作るには、Aシェフのレシピ、調理法、調理スタイルが必要です。保存され、尊重されるという意味です。この保存は記録のためにも重要ですが、新しいレシピを開発したり、誰かの食事制限に基づいて既存のレシピをチェックしたりする手段にもなります。

応用：ボラティリティの予測

これで、予測に応用できる可能性が見えてきました。価格帯の次の変化を予測することは、この連載で何度も検討してきたことであり、したがって予備的な説明は奇妙ではないかもしれません。ただし、要約すると、私たちはこの予測を使って、まずポジションのトレーリングストップを調整する必要があるかどうかを判断し、次にそれをどの程度調整する必要があるかを判断します。

この重要なツールであるナチュラリティスクエアの実装には、前々回の記事と同様、多層パーセプトロン(MLP)の助けを借りることになりますが、ここでの違いは、これらのMLPが、可換正方形を中心に構成されていることです。これによって、どの2本の足でも予想が出る可能性があるため、予想をチェックすることができます。正方形の4角は、将来のある時点における価格バーの幅の変化に関する異なる予測を反映しています。角Dに向かうほど、角Aは次のバーの範囲の変化を予測し、将来を見通すようになります。つまり、直近の価格バーの範囲の変化を使って、四隅を連動させるMLPを学習させることができれば、1本のバーだけでなく、もっと先の予測も可能になるということです。

私たちのNTを適用して予測を得るためのステップは、以下のコードで強調されています。

//+------------------------------------------------------------------+
//| NATURAL TRANSFORMATION CLASS                                     |
//+------------------------------------------------------------------+
class CTransformation
   {
      protected:
      
      public:
      
      CDomain<string>               domain;  //codomain object of first functor
      CDomain<string>               codomain;//codomain object of second functor
      
      uint                          hidden_size;
      CMultilayerPerceptron         transformer;
      CMLPBase                      init;
      
      void                          Transform(CDomain<string> &D,CDomain<string> &C)
                                    {
                                       domain=D;
                                       codomain=C;
                                       
                                       int _inputs=D.Cardinality(),_outputs=C.Cardinality();
                                       
                                       if(_inputs>0 && _outputs>0)
                                       {
                                          init.MLPCreate1(_inputs,hidden_size+fmax(_inputs,_outputs),_outputs,transformer);
                                       }
                                    }
      
      //
      void                          Let()
                                    {
                                       this.codomain.Let();
                                       this.domain.Let();
                                    };
      
                                    CTransformation(void){ hidden_size=1; };
                                    ~CTransformation(void){};
   };

まずは上記のNTクラスです。そして何気ない定義から、リンクしている2つの関手のインスタンスも含まれると予想されるが、それは当てはまったものの、十分に簡潔ではありませんでした。NTで重要なのは、関手によって写像される2つの領域であり、これらが強調されています。

//+------------------------------------------------------------------+
//| NATURALITY CLASS                                                 |
//+------------------------------------------------------------------+
class CNaturalitySquare
   {
      protected:
      
      public:
      
      CDomain<string>               A,B,C,D;
      
      CTransformation               AB;
      
      uint                          hidden_size_bd;
      CMultilayerPerceptron         BD;
      
      uint                          hidden_size_ac;
      CMultilayerPerceptron         AC;
      
      CTransformation               CD;
      
      CMLPBase                      init;
      
      
                                    CNaturalitySquare(void){};
                                    ~CNaturalitySquare(void){};
   };

上の図のようなナチュラリティスクエアは、NTクラスのインスタンスで示されるように、そのクラスも表現されます。A,B,C,Dで表されるその4つの角は、始域クラスによって捕捉されるオブジェクトであり、他の2つはNTとして認識されるため、その射のうち2つだけが直接MLPとなります。

MQL5での実践的な実装

MLPを使用するMQL5での実用的な実装は、主に学習方法と学習内容（ネットワーク重み）の保存方法において課題に直面することになります。この記事では、前の2稿とは異なり、訓練からの重みはまったく保存されません。つまり、新しいバーごとに、4つのMLPそれぞれの新しいインスタンスが生成され、訓練されます。これは以下のようにリフレッシュ関数で実装されています。

//+------------------------------------------------------------------+
//| Refresh function for naturality square.                          |
//+------------------------------------------------------------------+
double CTrailingCT::Refresh()
   {
      double _refresh=0.0;
      
      m_high.Refresh(-1);
      m_low.Refresh(-1);
      
      int _x=StartIndex();
      
      // atr domains capture 1 bar ranges       
      // bands' domains capture 2 bar ranges    
      // 1 functors capture ranges after 1 bar  
      // 2 functors capture ranges after 2 bars 
      
      int _info_ab=0,_info_bd=0,_info_ac=0,_info_cd=0;
      CMLPReport _report_ab,_report_bd,_report_ac,_report_cd;
      CMatrixDouble _xy_ab;_xy_ab.Resize(m_extra_training+1,1+1);
      CMatrixDouble _xy_bd;_xy_bd.Resize(m_extra_training+1,1+1);
      CMatrixDouble _xy_ac;_xy_ac.Resize(m_extra_training+1,1+1);
      CMatrixDouble _xy_cd;_xy_cd.Resize(m_extra_training+1,1+1);
      
      CElement<string> _e;
      for(int i=0;i<m_extra_training+1;i++)
      {
         ...
         
         if(i<m_extra_training+1)
         {
            _xy_ab[i].Set(0,_a);//in
            _xy_ab[i].Set(1,_b);//out
            
            _xy_bd[i].Set(0,_b);//in
            _xy_bd[i].Set(1,_d);//out
            
            _xy_ac[i].Set(0,_a);//in
            _xy_ac[i].Set(1,_c);//out
            
            _xy_cd[i].Set(0,_c);//in
            _xy_cd[i].Set(1,_d);//out
         }
      }
      
      m_train.MLPTrainLM(m_naturality_square.AB.transformer,_xy_ab,m_extra_training+1,m_decay,m_restarts,_info_ab,_report_ab);
     
      ...

      //
      if(_info_ab>0 && _info_bd>0 && _info_ac>0 && _info_cd>0)
      {
         ...
      }
      
      return(_refresh);
   }

上記のリフレッシュ関数は、ランダムな重みで初期化されたMLPを最近の価格バーだけで学習させます。これは、他の取引システムや共有コードの実装には明らかに不十分ですが、テスト目的でデフォルト値のゼロが維持されている入力パラメータ「m_extra_training」を上方調整して、予測をおこなう前により包括的なテストをおこなうことができます。

余分な訓練のためにパラメータを使用することは、EAにとってパフォーマンスの過負荷になるに違いなく、実際、この記事では訓練による重みの読み書きを全面的に避けた理由を指摘しています。

利点と限界

2022.08.01から2023.08.01までの日足時間枠でEURUSDのテストを実行すると、最良の実行の1つで以下のレポートが得られます：

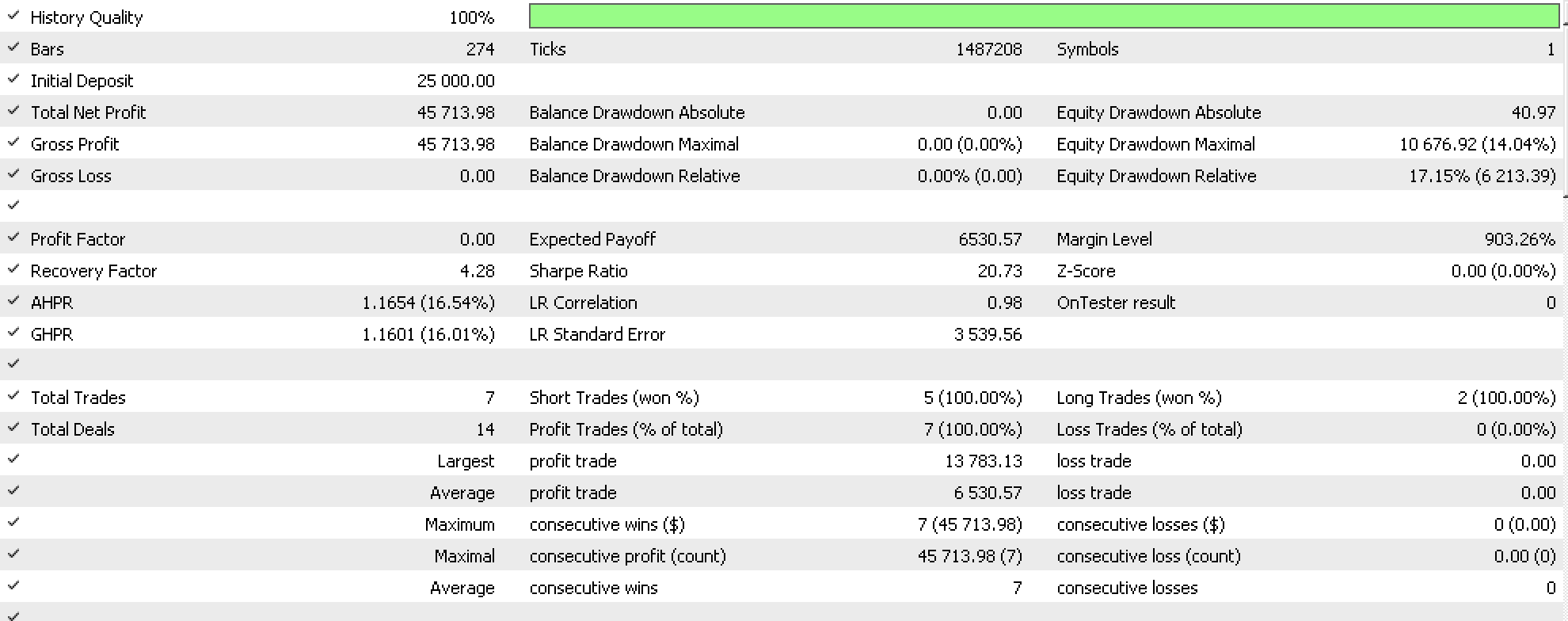
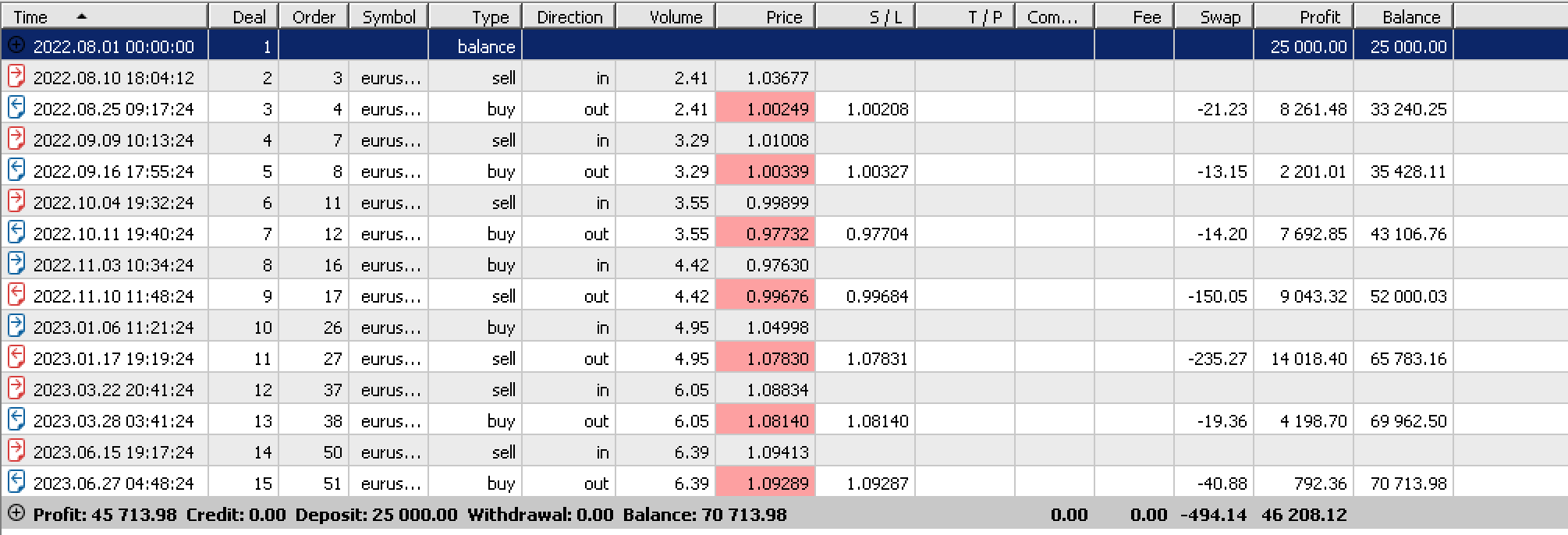
最適化されていない期間（私たちの場合、テスト範囲の1年前）に同じ設定でテストを実行すると、上記のレポートで得られた良好なパフォーマンスを反映しない否定的な結果が得られます。ご覧のように、すべての利益はストップロスによるものです。

ボラティリティを予測する上で、この連載で以前に使用したアプローチと比べると、このアプローチは確かにリソースを必要とし、最適化されていない期間をフォワードウォークできるようにするために、自然性の正方形における4つのオブジェクトの定義方法を変更する必要があることは明らかです。

結論

ここに要約すると、重要な概念は「自然変換」です。これらは、圏をリンクする関手の平行対の違いを捉えることによって、圏をリンクする上で重要な意味を持ちます。ここで検討された用途は、ナチュラリティを利用したボラティリティの予測でしたが、他の用途としては、エントリシグナルやエグジットシグナルの生成、ポジションサイジングなどが考えられます。加えて、この記事とこの連載を通して、得られた最適化されたセッティングでフォワードランはおこなっていないことを述べておくといいでしょう。そのため、そのまま（つまり提供されているコード通りに）機能しない可能性もありまが、読者が使うかもしれない他の戦略とこれらのアイデアを組み合わせるなど、一旦修正を加えれば機能する可能性があります。MQL5のウィザードクラスを使うと、このようなことがシームレスにできるので便利です。

参考文献

共有されているウィキペディアとStack Exchangeのハイパーリンク。

添付ファイルに関する注意事項

TrailingCT_18_.mqhをMQL5\include\Expert\ Trailing\フォルダに配置して、ct_18.mqhをMQL5\include\フォルダに配置してください。

さらに、EAの一部としてそれらを組み立てる必要があるため、ウィザードを使用してEAを組み立てる方法について、こちらのガイドに従ってください。記事にあるように、トレーリングストップなしで、固定証拠金を資金管理に使いました。どちらもMQL5のライブラリの一部です。いつものように、この記事の目的は、聖杯を紹介することではなく、読者自身の戦略にカスタマイズできるアイデアを紹介することです。