非線形指標

はじめに

非線形手法は金融時系列を扱うのに広く使われています。特に、MetaTrader取引プラットフォームには、非線形なアプローチを使用する指標がかなり多くあります。すべてが取引に積極的に使用されています。

一般的な情報よりもシグナルの特定の特性が重要な場合、非線形指標が必要になることがあります。また、非線形指標は、線形指標が無力な状況に対応することができます。

非線形指標を作るのは比較的簡単な作業です。通常の線形指標は、以下の式で記述することができます。

ここで、w[i]は指標の重み係数です。次に、この指標を非線形化します。そのために、価格そのものではなく、価格の対数を使うことにします。和を計算した後、その指数を求めてみます。

このやり方は、一見シンプルに見えます。ただし、指標の計算方法は大きく変更されます。すべての乗算は指数関数に変換され、加算は乗算に置き換えられます。例えば、算術平均(SMA)は幾何平均に置き換えられます。

また、対数の使用は、計算に正の数が使われていることを端的に示しています。この価格変換は、あらゆる線形指標で使用することができます。自分で簡単にできます。同時に、係数に関するすべての要件は、線形指標と同じままです。この記事で紹介した指標のテンプレートを、対数のバージョンに変換してみましょう。

しかし、時系列自体の変換を利用して非線形指標を構築することも可能です。今回は、そんな指標について考えてみたいと思います。この記事はArraySort関数に特化していると言えます。これは新しい指標の基礎となるものです。

中心的傾向の測定

中心的傾向は、データセットの典型的な値です。中心的傾向の最も一般的な尺度は、算術平均、中央値、最頻値です。算術平均は線形尺度であり、単純移動平均に実装されています。中央値と最頻値は非線型です。

中央値はデータセットを2つに分割します。1つ目の半分には中央値より小さい値、2つ目には中央値より大きい値が含まれています。中央値の算出方法について見てみましょう。一連の数値1, 6, 9, 3, 3, 7, 8.があるとします。これらの数字を昇順に並べ替えると1, 3, 3, 6, 7, 8, 9.になり、中央値はこの系列の中心にある数字となります。この例では、この数値は6です。データが偶数の場合、中央値は中心に近い数字の和の半分になります。例えば、1, 3, 3, 6, 7, 8の場合、中央値は (3 + 6)/2 = 4.5となります。中央値の最大の特徴は、スパイクに対して非常に強いということです。

最頻値は、データサンプルの中で最も頻繁に出現する値です。例えば、サンプル1, 6, 9, 3, 3, 7, 8では、最も多い数字は3で、これが最頻値となります。ただし、価格を分析する場合、各値は一度しか発生しないため、最頻値を計算するためには、Pearsonの経験式を用いることができます。

Mode = 3*Median – 2*Mean

この式によると、最頻値は不安定な指標です（係数が区間-1...+1の境界を越えている）が、他の指標に加えるものとして有用です。

もう1つの中心的な指標は、その中間と考えることができます。これを計算するには、時系列の最大値と最小値の半値和を求める必要があります。ミドルレンジはスパイクに敏感で信頼性が低いですが、一部の指標で使用されています。

中心的傾向を示す4つの指標すべては、チャート上では次のようになります。

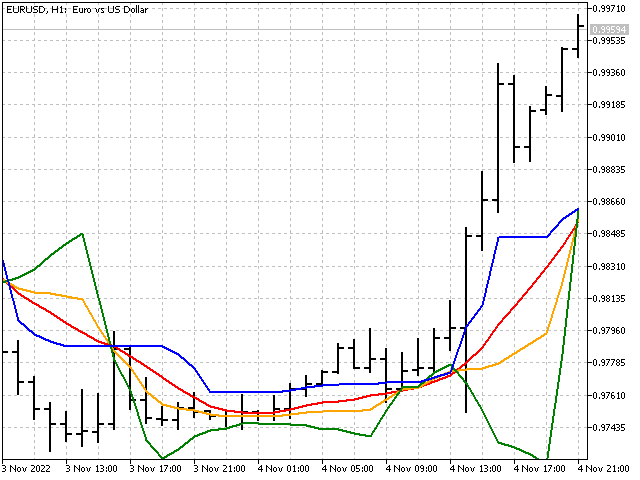
ベイズスムージング

中央値のグラフを見ると、中央値がかなり長い間変化していない部分があることがわかります。中央値の期間が長いほど、そのような領域は顕著になります。例えば、中央値を51とした場合のグラフは次のようになります。

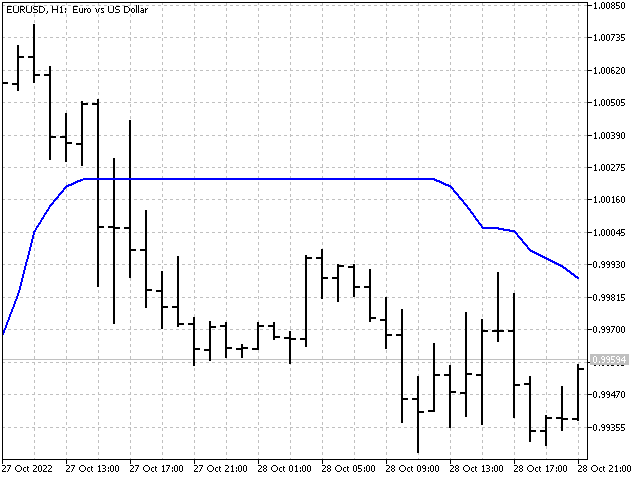
中央値を価格変動に対してより敏感にするようにしたらどうでしょうか。例えば、中央値と単純平均の和を半分にし、中央値と移動平均の安定性を合わせることができます。このオプションは可能ですが、少し違う方法で、ベイズスムージングを使うことを提案します。

まず、すべての価格の合計を計算する必要があります。

sum = price[1] + … + price[n].

次に、スムージングをおこなう相対的な値を選択する必要があります。そうすると、ベイズ平均は以下の式で計算できます。

ここでpは、選択した値の影響の強さを設定するためのパラメータです。その値は少なくとも1でなければなりません。例えば、中央値、範囲の中央値、最大値、最小値を選んでいます。

ベイズスムージングは、複数の値に対して適用することも可能です。その場合、その方程式は次のようになります。

指標では、このオプションは最大値と最小値で表示されます。チャートで見るとこんな感じです。

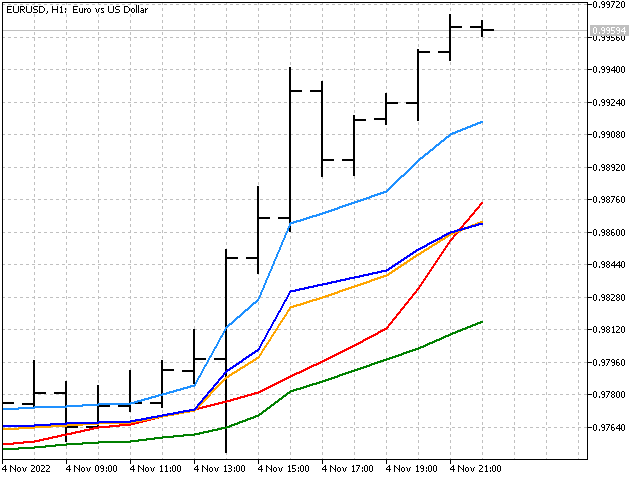
ベイズスムージングを適用することで、線形と非線形の手法を1つの指標に組み合わせることができることがわかります。

中央値の中央値

三角窓関数の求め方を思い出してみましょう。期間3の単純移動平均を基準にします。ここで、3本の移動平均を1本分ずらした値を求める必要があります。

 

あとは、この3つの値の平均を求めればよくなります。

次に、同じ原理を中央値にも適用してみましょう。まず、3つの中央値の値を求めます。

そうすると、指標値はこれらの中央値に等しくなります。

チャート上ではこのように表示されます。

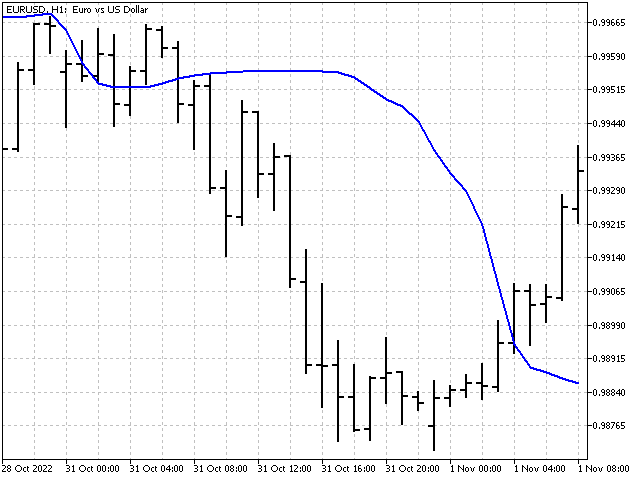
擬似中央値

擬似中央値の計算アルゴリズムは、前のものと少し似ています。唯一の違いは、各ステップにおいて、部分配列の中央値ではなく、最大値と最小値を探すということです。

 

ここで、見つかった高値から最小値を、安値から最大値を取る必要があります。その平均値が擬似的な中央値となります。

疑似中央値は、中央値と範囲の中央値の両方の代用となります。

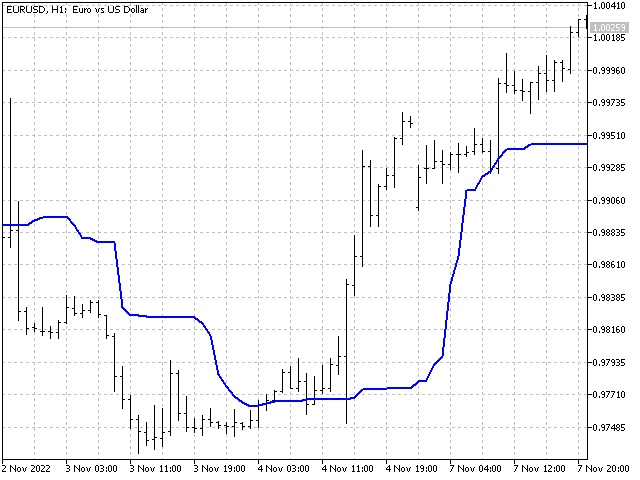
指標は非直線性で駄目にならない

トレンドの強さ： 例えば線形加重平均のような、際立ってトレンドに着目している指標を取り上げてみましょう。指標値は以下のように算出されます（指標期間を5とする）。

次に、これらの価格から2つの新しいシーケンスを作成します。最初のシーケンス（p[]とする）では、価格は昇順（低いものから高いもの）に並び替えます。2番目のシーケンス(P[])では、価格の降順で並び替えます。次に、これらの配列にLWMAの重みを適用してみましょう。

 

新しい値を2つ得ました。これは、価格が厳密に正確な上下トレンドを形成した場合に、指標の値がどのようになるかを示しています。

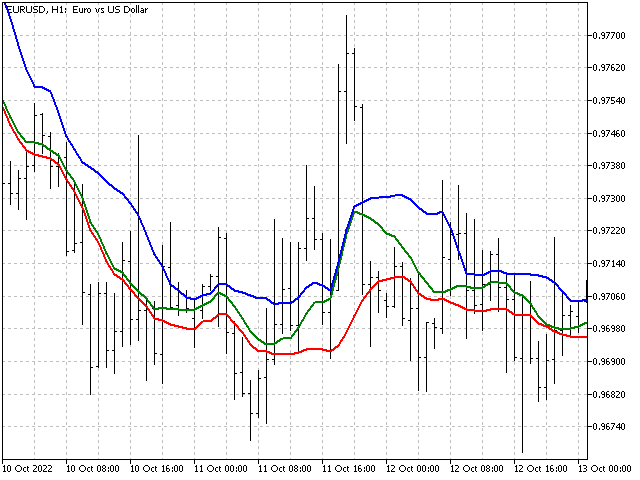
これで、トレンドの強さを視覚的に評価できます。指標が下限または上限に近づくほど、強気または弱気のトレンドが強くなります。また、上下のラインの差は、市場のボラティリティを示唆するものです。互いに離れているほど、ボラティリティは高くなります。

相対強度指数(Relative Strength Index)RSIは、J. Welles Wilderによって開発され、1978年6月に雑誌Commoditiesに発表されました。この指標を算出するために、2つの補助変数UとDを使用します。これらは上下の値動きを分けるために必要なものです。

U値とD値を算出した後、その値に対して指数平滑化をおこないます。この場合、指標となる数値は

です。

これは、時間によって証明された優れた指標とで、すでに非線形です。価格差を入力する、または、ゼロが指標入力に送られます。価格の差の代わりにその発生確率を使って、非線形性を別のものに変えてみましょう。直感的には、大きな偏差の方が小さな偏差よりも少ないように思います。ちょっとしたテストで、直感は欺けないということがわかりました。

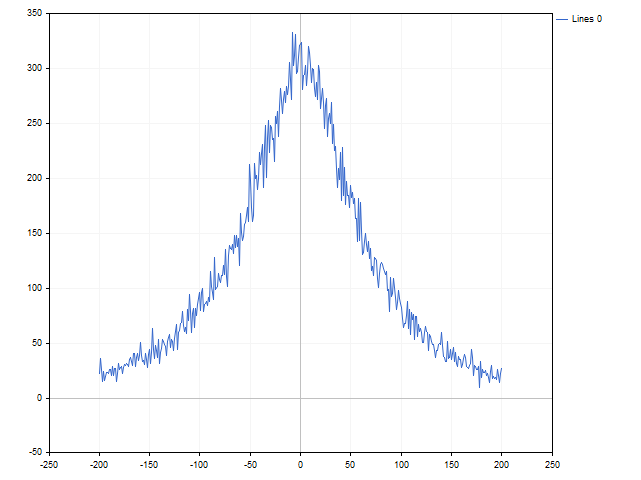
価格差の代わりに、以下の値を使用することにします。

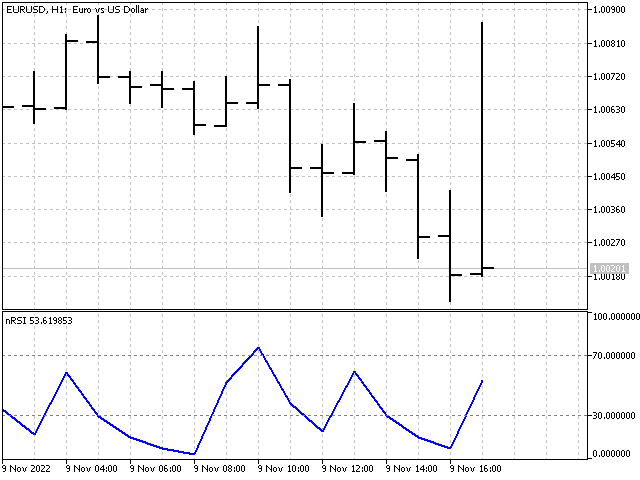
ここで、nはこの差が歴史上何回発生したかを示し、Nは全観測回数を表します。この場合、指標式は次のようになります。

指標自体は以下のように表示されます。

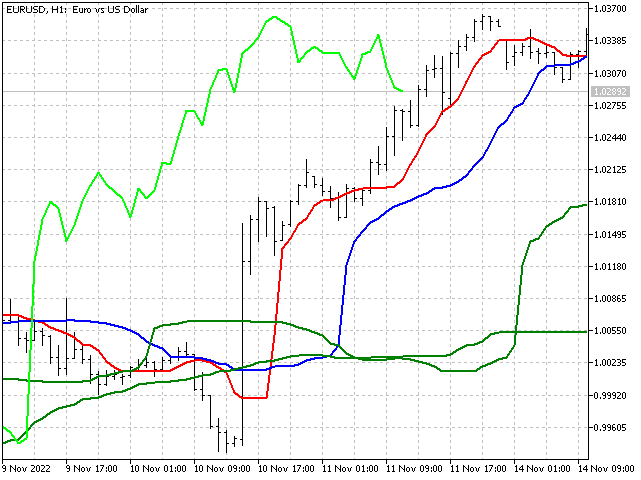
一目均衡表.： この指標は、日本のアナリスト、細田剛一氏が開発したものです。一目均衡表は、市場分析におけるいくつかのアプローチを組み合わせたものです。この指標は、レンジの真ん中を使用して、転換線、基準線、先行スパンをプロットします。それらをより安定した指標である中央値に置き換えてみましょう。加重中央値で先行スパンAを算出します。これらの置き換えは、指標の本質に影響を与えず、かつ、より安定したものにする必要があります。修正版の一目均衡表の線はこんな感じです。雲は自分で描いてください。

ローソク足パターン

テクニカル分析には、日本のローソク足とその組み合わせの研究に基づく、1つの興味深い方向性があります。これにはかなり多くの記事が割かれています。例は、「ろうそく足パターンの分析」です。

ここでは少し趣向を変えて、順序統計学を用いてローソク足のパターンを識別してみることにします。実際にどのようなアクションを起こすか、見てみましょう。

まず、分析に使用する価格の順番を設定する必要があります。そして、選択した地点の価格値を記録していきます。その後、価格順序を示すインデックスを保存します。

価格	値	インデックス
Open[0]	1.03248	0
Low[1]	1.03133	1
High[1]	1.03204	2
Open[1]	1.03204	3
Low[2]	1.03191	4
High[2]	1.03256	5
Open[2]	1.03248	6
Low[3]	1.03217	7
High[3]	1.03296	8
Open[3]	1.03292	9

次に、価格の値を昇順に並び替える必要があります。

1.03133	1
1.03191	4
1.03204	3
1.03204	2
1.03217	7
1.03248	6
1.03248	0
1.03256	5
1.03292	9
1.03296	8

次に、価格が一致したときに起こりうる曖昧さを解消する必要があります。そのためには、値の小さい方のインデックスを配列の先頭に近づけます。この例では、(3, 2)と(6, 0)のインデックスペアが入れ替わっています。

その後、インデックスシーケンスを解析します。解析の便宜上、指標を1つの数値、8956073241に変換します。この数字がパターンの最終的な特徴となります。分析に10以上の値を使用する場合は、1つの数値を組み立てる際に、適切な数の基数を使用する必要があります。

コードでは、こんな感じのアルゴリズムになります。

   int array[10][2];//array for writing values and indices

   /*fill the array*/
   array[0][0]=(int)MathRound(iOpen(_Symbol,PERIOD_CURRENT,1)/_Point);
   array[0][1]=0;
   for(int j=0; j<3; j++)
     {
      array[3*j+1][0]=(int)MathRound(iLow(_Symbol,PERIOD_CURRENT,j)/_Point);
      array[3*j+1][1]=3*j+1;
      array[3*j+2][0]=(int)MathRound(iHigh(_Symbol,PERIOD_CURRENT,j)/_Point);
      array[3*j+2][1]=3*j+2;
      array[3*j+3][0]=(int)MathRound(iOpen(_Symbol,PERIOD_CURRENT,j)/_Point);
      array[3*j+3][1]=3*j+3;
     }

   ArraySort(array);

   /*eliminate possible ambiguities when prices match*/
   for(int j=1; j<10; j++)
      if(array[j-1][0]==array[j][0] && array[j-1][1]>array[j][1])
        {
         int v=array[j-1][1];
         array[j-1][1]=array[j][1];
         array[j][1]=v;
         j=1;
        }

   /*gather the number*/
   ulong number=0;
   for(int j=0; j<10; j++)
      number=number+array[j][1]*(ulong)MathRound(MathPow(10,j));//10 - number system base

このスクリプトを使って、パターンの数と履歴で何回発生したかを推定することができます。

このアルゴリズムの唯一の欠点は、スケーリングに鈍感なことです。ローソクを縦に伸ばしたり縮めたりしても、パターンは変わりません。例えば、この3つの状況は同じだと認識されました。

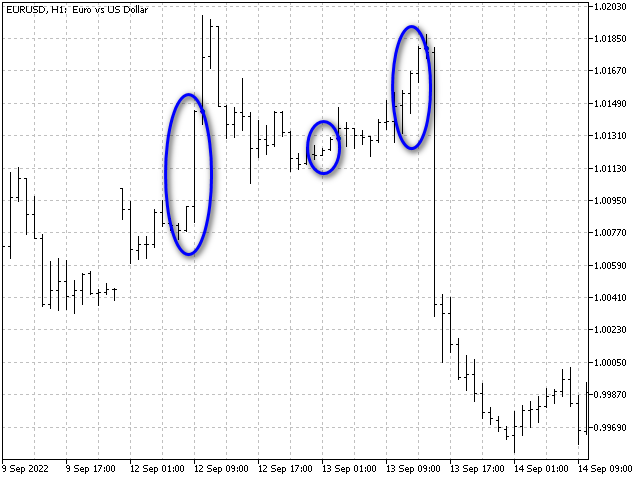
ただし、この欠点は、このアルゴリズムに基づいた指標を作ることを妨げるものではありません。指標には少し予測させましょう。各パターンについて、そのパターンに続くバーの高値-始値、始値-安値の差の合計を累積していきます。このパターンが再び現れたとき、指標はどちらが多いかを評価し、予測をおこないます。結果、次のようになります。

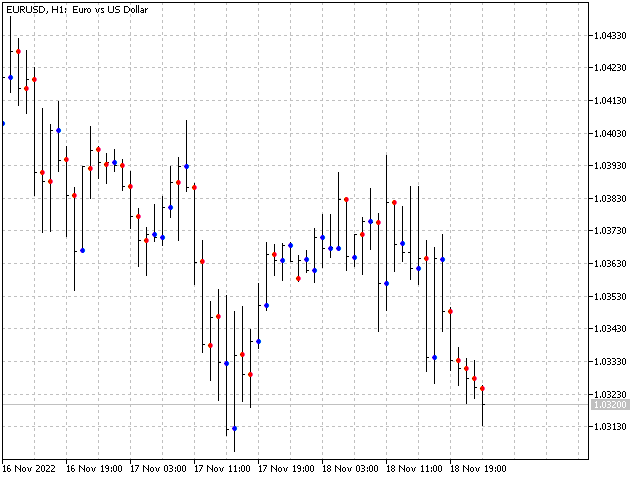
Alongとacross

上記で得たアルゴリズムは、取引システムを作成する際にも利用することができます。2つの簡単な例を見てみましょう。

Along：多くの場合、取引システムのシグナルは、指標の現在の値に基づいています。ポジションを建てるためのシグナルを生成するために、その前の値をある数だけ使用するとどうなるでしょうか。例えば、過去10個の指標値を取り出して、パターン構築アルゴリズムを適用することができます。すると、出来上がったパターンは、指標値の経時変化を示すことになります。例えば、過去10回の始値を使ってパターンを探しました。また、予測の水平軸を5本先まで伸ばしました。このEAの取引はこのような感じです。

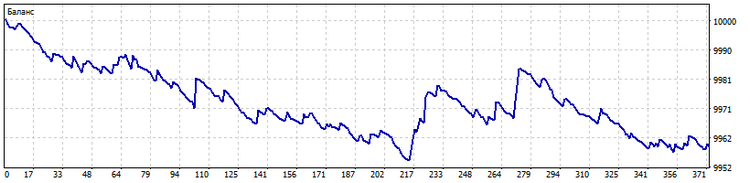
Across.また、パターン計算アルゴリズムは、指標群に対して使用することができます。この場合、パターンは、指標が互いに相対的に配置されている順序を示すことになります。この順序によって、取引システムのシグナルが決定されます。例として、2*n + 1 (n = 0…9)の期間を持つ10本の移動平均を使用しました。この場合の取引はこんな感じです。

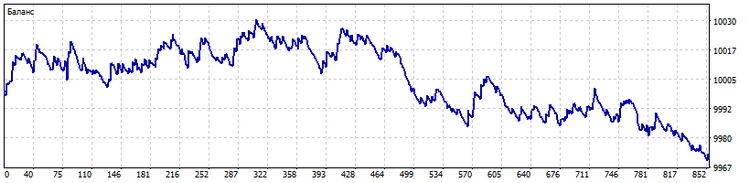
どちらの場合も、アルゴリズムが認識するパターンの数を制御する必要があります。その数は決して少なくないはずです。その場合、取引システムは異なる状況を互いに区別できない可能性があります。また、パターン数が多すぎると、取引状況がユニークと認識され、取引システムが対応できなくなるため、パターン数は多くできません。また、2番目のケースでは、互いにできるだけ異なる指標を用いる必要があります。例えば、わずかな期間の違いでも単純な移動平均線しか使わないのは、明らかに開発者のミスですが、それでも頑張ったことは褒めます。

結論

市場情報を処理する非線形手法は、指標と取引戦略の両方で使用することができます。以前から使われていたものだから、今も使えます（使うべきです）。非線形指標は、値動きを改めて見直すのに役立ちます。取引システムで非線形アプローチを使用することで、質的に異なるシグナルを得ることができるようになります。

記事で使用されているプログラム

名前	タイプ	簡潔な記述
Base LogIndicator	指標	物価の対数変換に基づく指標 （InpCoefficient - 指標の重み（任意の数値を入力可能、合計はゼロであってはならない）
MMMM	指標	中心的傾向を示す指標（iMode - 傾向の選択、iPeriod - 指標の期間（2以上））
Bayesian Moving Average	指標	ベイジアンスムージングを実装する指標（iMode - 平滑化のための傾向の選択、iPeriod - 指標の期間、 Parameter - 平滑化パラメータ）
Median Median	指標	中央値の中央値を表示する指標。三角窓関数の非線形アナログ（iPeriod - 指標期間）
Pseudomedian	指標	場合によっては、疑似中央値が中央値と範囲の中間の良い置き換えになることがある（iPeriod - 指標の期間）
Strength Trend	指標	価格サンプルのトレンド成分がどの程度強いかを示す指標(iPeriod - 指標期間)
nRSI	指標	価格上昇の確率に基づく指標(iMode - スムージング手法の選択、iPeriod - 指標の期間)
nIchimoku Kinko Hyo	指標	従来の一目指標を近代化した例’PeriodS、PeriodM、PeriodL - 短期、中期、長期の指標期間）
Script Pattern	スクリプト	価格パターンの統計情報を収集するスクリプト。最終結果は、Filesフォルダのファイルに保存
Pattern	指標	パターンを計算する指標。過去のデータに基づき、オープニングバーでの優勢な値動きを予測 （Least - 履歴の中のパターン観測の最小数。Least回以上観測されたパターンでのみ予報を表示）
EA Along Across	EA	価格パターンを利用した取引EA （Mode - パターン方向の選択、 Least - 履歴の中のパターン観測の数、 Percent - 開かれたポジションの数に影響を与える、ある方向の値動きが他の方向より優位である割合（51～99の範囲で選択））