Pourquoi y a-t-il de telles astuces avec les diplômes ? - page 2

[Andrey Azatskiy]

Roman:

-0,2 n'est pas zéro pour renvoyer une erreur de division par zéro.

La fonction renvoie -nan, c'est-à-dire Not a Number (pas un nombre), et l'erreur se produit lorsqu'on essaie de diviser par -nan. Le texte d'erreur n'est tout simplement pas approprié.

[[Supprimé]]

Solution correcte :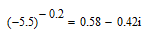 la solution est dans le domaine complexe.

Mais si nous parlons d'avoir des branches de solutions différentes pour les paramètres d'entrée positifs et négatifs, nous devons d'abord définir ces branches :

.

Créez une telle fonctionnalité et tout ira bien ;)

[Roman]

Andrey Azatskiy:

La fonction renvoie -nan, c'est-à-dire Not a Number (pas un nombre), et une erreur se produit lorsqu'on essaie de diviser par -nan. Le texte d'erreur n'est tout simplement pas approprié.

Pourquoi diable -0,2 serait-il -nan ?)

Une autre fonction de test

En calculatrice.

1/(-3 ^ 3)

-27

Dans les fonctions mql

double n = 1.0/MathPow(-3.0, 3.0);
Print(n);

-0.03703703703703703

[Andrey Azatskiy]

Roman:

Alors pourquoi diable -0,2 est un nan ?)

Une autre fonction de test

Dans une calculatrice

Dans une fonction mql.

n'est pas -0,2 - nan, mais le résultat d'une augmentation de degré.
Le degré fractionnaire d'un nombre (a^m/n) est la racine de degré n de a^m.
Si la valeur de la racine secondaire est négative, elle peut être soit négative soit positive, en fonction de la puissance de m et du nombre a lui-même (qui, dans mon problème, est toujours négatif, donc positif pour une puissance de m positive et négatif pour une puissance négative). Ainsi, si la valeur de la sous-racine est négative, alors le nombre est également négatif. La racine d'un nombre négatif se trouve dans la zone complexe, nous ne pouvons donc pas opérer sur les valeurs de la zone complexe viale type double habituel, c'est pourquoi l'implémentation standard du degré donne -nan.

[Andrey Azatskiy]

Олег avtomat:

Solution correcte : la solution est dans le domaine complexe.

Mais si nous parlons d'avoir différentes branches de solutions pour les paramètres d'entrée positifs et négatifs, alors nous devons d'abord définir ces branches :

.

Créez une telle fonctionnalité et tout ira bien ;)

Merci pour votre réponse détaillée. Mais pour moi, le calcul complexe ne convient pas à mon problème, donc je me limiterai très probablement aux nombres naturels et, par conséquent, je ne tomberai pas dans le domaine complexe.

[[Supprimé]]

Andrey Azatskiy:

Merci pour votre réponse détaillée. Mais pour moi le calcul complexe n'est pas adapté à mon problème, donc je vais probablement me limiter aux nombres naturels et par conséquent je ne tomberai pas dans le domaine complexe.

C'est ce dont je parle, et je vous ai spécifiquement montré un exemple. Regardez-le attentivement. Cet exemple correspond exactement à votre cas.

zy

la traduction en µl est très facile

[Roman]

Andrey Azatskiy:

n'est pas -0,2 - nan, mais le résultat d'un degré.
La puissance d'un nombre fractionnaire (a^m/n) est la racine de degré n de a^m.
Si la valeur de la racine secondaire est négative, elle peut être négative ou positive en fonction de la puissance de m et du nombre a lui-même (qui dans mon problème est toujours négatif, donc il est positif à la puissance positive de m et négatif à la puissance négative). Ainsi, si la valeur de la sous-racine est négative, alors le nombre est également négatif. La racine d'un nombre négatif se trouve dans la zone complexe, nous ne pouvons donc pas opérer sur les valeurs de la zone complexe via le type double habituel, c'est pourquoi l'implémentation standard du degré donne -nan.

Andrey, oui, je me suis mal exprimé, il est clair que le résultat de l'élévation à une puissance renvoie -nan.
Mais ce résultat donne lieu à une puissance fractionnaire, où l'entier est zéro -0,2
La calculatrice calcule tout correctement.

Et le test précédent, lui aussi, ne compte pas comme dans la calculatrice.

[Andrey Azatskiy]

Олег avtomat:

C'est de ça que je parle, et je vous ai donné un exemple précis. Regardez bien.

Oui, je l'ai. Merci. (même la formule est écrite)

[Aleksey Nikolayev]

Andrey Azatskiy:

Peut-être les jambes proviennent-elles du fait que l'on ne peut pas prendre une racine paire à partir d'un nombre négatif ? Je suis déjà un peu confus... Et surtout, comment le contourner ?

Les degrés entiers sont déterminés simplement par multiplication (et en prenant l'inverse pour les exposants négatifs), ils sont donc facilement transférables aux bases négatives. Les degrés fractionnaires sont définis via le logarithme et l'exposant : y^x=exp(x*ln(y)) et avec des nombres négatifs, on arrive au plan complexe. Le logarithme a un nombre infini de branches et pour éviter de s'embêter à trouver la bonne branche, ils renvoient NAN.

[Igor Makanu]

Andrey Azatskiy:

Merci pour votre réponse, mais en général, si l'on prend une solution arithmétiquement correcte, il semble que seuls les nombres complexes puissent être utilisés pour mettre en oeuvre une telle solution... Dans la méthode que vous proposez, il est nécessaire de casser le degré pour que la valeur sous-jacente ait toujours un degré positif et que la réponse soit toujours positive. Mais si l'on se passe de cet ajustement - nous n'en arrivons qu'aux nombres complexes, en fait selon le modèle algébrique généralement admis à ma connaissance (je ne suis pas mathématicien de formation) - la racine d'un nombre négatif sera un nombre complexe.

utilisez la formule que j'ai suggérée ci-dessus.

Voici la même formule :

void OnStart()
  {
   int m = 2;
   int n = 10;
   
   double result = 1.0/pow(pow(-5.5,m),1.0/n); 		// result = 0.7110947333604484
   Print("result = ",result);
  }

et voici un exemple de la façon de convertir un double en fraction

https://www.mql5.com/ru/forum/290279#comment_9396706