Le phénomène de Saint-Pétersbourg. Les paradoxes de la théorie des probabilités. - page 2

Nouveau commentaire
 
Vitalii Ananev:

:) Le même stratagème a été utilisé dans le passé par des escrocs, et il est probable qu'il le soit aussi aujourd'hui par des escrocs de toutes sortes. L'essentiel pour eux est que la victime leur remette l'argent et ils ne le récupéreront jamais.

Et une fois, j'étais dans un marché de voitures à Yuzhny Port quand ils ont "pris" un pigeon pour trois cartes...

C'est assez difficile à dire. À un moment donné, j'étais sûr que ce con allait gagner...

Après ça, un jour, je rentrais tard chez moi en voiture. Il y a très peu de gens en dehors du métro... ... et il y a des gars assis autour, et ils jettent ces trois cartes. Je décroche et leur raconte brièvement l'histoire, suivie de la question "Comment faites-vous ?". Il s'avère que c'est simple. Toutes les cartes ont un petit coup de pouce pour plier un coin que le croupier n'a pas vu... ...mais en fait, il a tourné le coin d'une autre carte, et celle qui a été tournée, par un faux joueur, il l'a retournée.

  
//+------------------------------------------------------------------+
//|                                                          SPp.mq5 |
//|                        Copyright 2017, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2017, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
//--- input parameters
input int      bet=4;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart(){
   
   double me=0;
   double bank=0;
   
   while(!IsStopped()){
      
      
      double z=1.0;
      
      while(!IsStopped()){
         if(MathRand()/32768.0<0.5){
            // I win
            z=MathMin(bet,z);
            me+=z;
            bank+=(bet-z);
            break;
         }
         else{
            z*=2.0;
         }
      }
      
      Comment("Me: ",(string)me,", bank: ",(string)bank);
   
   }
   
   Comment("");

}

Avec une mise de 4, le jeu semble être sur un pied d'égalité (si je comprends bien les règles du jeu).

 
Alexey Viktorov:

Et j'ai vu une fois un idiot se faire "acheter" trois cartes dans un marché de voitures à South Port...

C'est assez difficile à dire. À un moment donné, j'étais sûr que ce con allait gagner...

Après ça, un jour, je rentrais tard chez moi en voiture. Il y a très peu de gens en dehors du métro... ...et il y a ces gars assis là qui jettent ces trois cartes. Je décroche et leur raconte brièvement l'histoire, suivie de la question "Comment faites-vous ?". Il s'avère que c'est simple. Toutes les cartes ont un petit coup de pouce pour plier un coin que le croupier n'a pas vu... ...mais en fait, il a tourné le coin d'une autre carte, et celle qui a été tournée, par un faux joueur, est non tournée.

En fait, c'est beaucoup plus simple que ça. Autour du "brancard" se frottent toujours ses assistants, alias les appelants, qui jouent aussi, parfois gagnent, parfois perdent. En général, ils créent l'apparence du fair-play. Une personne aléatoire qui fait un pari dans ce jeu, même si elle devine, ne récupérera pas son argent. Peu importe qu'il y ait 3 cartes ou 3 verres et une balle, dès qu'un joueur ouvre une carte ou soulève un verre, ces aides se penchent prétendument pour regarder de plus près, bloquant ainsi la vue des témoins occasionnels. Si le joueur devine, il suffit de le contester en disant non, il ne le fait pas. Si un "pigeon" est très indigné, ils peuvent même lui donner un coup de pied dans le cou. Le "katala" lui-même n'a même pas besoin de faire des efforts pour embrouiller le joueur, sa fonction est d'obtenir la mise.

 
Novaja:
Le phénomène de Saint-Pétersbourg
c'est comme la radio que l'on dit avoir été inventée par Popov.

la martingale habituelle...
 
hartmann:
c'est comme la radio que l'on dit avoir été inventée par Popov.

une martingale régulière...

inhabituel

 
Vitalii Ananev:

En réalité, c'est beaucoup plus simple que cela. Autour du "gourdin", il y a toujours ses assistants, alias les appâteurs, qui jouent aussi, parfois en gagnant, parfois en perdant. En général, ils créent l'apparence du fair-play. Une personne aléatoire qui fait un pari dans ce jeu, même si elle devine, ne récupérera pas son argent. Peu importe qu'il y ait 3 cartes ou 3 verres et une balle, dès qu'un joueur ouvre une carte ou soulève un verre, ces aides se penchent prétendument pour regarder de plus près, bloquant ainsi la vue des témoins occasionnels. Si le joueur a deviné, il le conteste simplement en disant non non. Si un "pigeon" est très indigné, ils peuvent même lui donner un coup de pied dans le cou. Le "katala" lui-même n'a même pas besoin de faire des efforts pour embrouiller le joueur, sa fonction est d'obtenir la mise.

Avez-vous personnellement vu un joueur faire un pari mais ne pas lui donner les gains ? Je n'ai jamais vu personne gagner, sauf leurs complices.

Ces trois cartes ou trois dés à coudre, selon la théorie des probabilités, sont gagnables pour les organisateurs du jeu, et puis il y a les tours de passe-passe.

 
hartmann:
c'est comme la radio que l'on dit avoir été inventée par popov.

une martingale régulière...

Mais quel chic MO, gagnant l'infini !

 
Novaja:

Mais quel magnifique MO, gagnant l'infini !

Ici, j'ai fait le calcul.
pour 100 000 jeux, le chiffre est de 8,32 roubles.
pour un million de jeux, c'est un nombre de 25,76 roubles.

Plus il y a de jeux, plus le nombre est élevé.
C'est comme la martingale : plus vous jouez, plus vous avez de chances de perdre.
Dossiers :
5mro81.zip  3420 kb
 

Les conditions du jeu ne sont pas entièrement décrites, comme d'habitude.

Est-il possible de gagner plus que sa mise ? Sinon, il n'y a aucun intérêt à jouer.

Alors il devrait être autorisé à gagner sur le pot. Il suffit donc de faire la mise minimale, il y aura un gain.

Peut-être que la condition est que vous pouvez jouer une fois, et ici nous devons décider de la mise, afin qu'il y ait la probabilité maximale de gagner.

Comme tous les "pradlocks" - à partir de conditions incomplètes.

Solution :

Il n'est même pas question de parier. Pari 1. Cela n'a plus de sens, la probabilité de gagner ne dépend pas de la taille de la mise. Donc 1, juste pour commencer le jeu.

Alors quel est le paradoxe ? En partant du principe qu'il faut miser plus pour augmenter ses gains ? C'est peut-être ça.

 
Novaja:

Mais quel magnifique MO, gagnant l'infini!

il s'agit d'une fonction non linéaire.
y=2^x.


et où tend Y dans une fonction non linéaire si X tend vers l'infini ? c'est ça, vers l'infini.



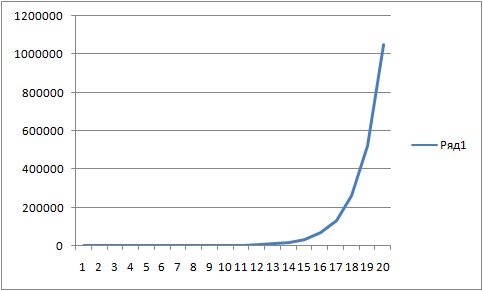
donc si le nombre de parties = infini, alors le gain moyen = infini.

Et le problème est également réglé de telle sorte que ses pertes sont une fonction linéaire (toujours 25 roubles chacune), et ses gains une fonction non linéaire.

Vous devez tracer deux fonctions. Le premier graphique sera d'abord plus élevé que le second, puis ils échangeront leurs places.

Tout dépend du nombre de jeux.
123456789...25
Nouveau commentaire