Le phénomène de Saint-Pétersbourg. Les paradoxes de la théorie des probabilités. - page 4
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Dans ce fil, veuillez poster tous les paradoxes de la théorie des probabilités que vous pouvez trouver.
Gabor Sekei. Paradoxes en théorie des probabilités et en statistique mathématique.
http://baguzin.ru/wp/wp-content/uploads/2016/05/Габор-Секей.-Парадоксы-в-теории-вероятностей-и-математической-статистике.pdf
Mais que se passe-t-il si c'est de 0 à 5, ou 7, ou tout autre nombre ? Vous devez encore diviser par 32768.0. Ou y a-t-il des options ?
C'est bien sûr ce qu'il faut faire :
Novaja:
В этой теме прошу выкладывать разные парадоксы теории вероятности, все, какие можно найти.
Puzzles mathématiques et divertissement
Ce livre du célèbre vulgarisateur scientifique américain M. Gardner contient de nombreux problèmes et énigmes très divertissants issus de différentes branches des mathématiques. Une sélection réussie du matériel, une forme de présentation tout à fait inhabituelle et l'humour subtil de l'auteur apporteront un grand plaisir à un large éventail de lecteurs - des amateurs de mathématiques qui veulent passer utilement leur temps libre.
Source :
Gardner M. 'Mathematical puzzles and fun'. \\Traduit de l'anglais par Danilov Y.A., édité par Smorodinsky Y.A. - Moscou : Mir, 1971 - p.511
C'est, bien sûr, ce qu'il faut faire :
Sans utiliser le reste de la division.
Sans utiliser le reste de la division.
Je pense que le "non-aléatoire" n'était vraiment perceptible que lors de la définition de pair, impair.
Si vous utilisez un reste de division à partir de nombres bien plus grands que 2, il est peu probable qu'il soit détectable.
La seule façon correcte est d'utiliser des nombres qui sont 2 à la puissance de N au lieu de 100, par exemple 64, 128, 256...
Mais la réduction de rand() au double de 0 à 1 est également normale, car elle est plus facile à comprendre une valeur aléatoire et plus précise, bien qu'un peu plus lente. Mais je pense que nous parlons de fractions de nanoseconde, bien que cela puisse être des nanosecondes, parce que le processeur doit passer des opérations int aux opérations doubles(mélange FPU/ALU), et Renat a dit une fois que cela est loin d'être gratuit.
Dans ce fil, veuillez poster tous les paradoxes de la théorie des probabilités que vous pouvez trouver.
https://oschool.ru/files/studys/55df78bc740d76b70e8b4287/1443032585656.pdf
Avez-vous déjà vu un joueur faire un pari et ne pas recevoir ses gains ? Je n'ai jamais vu personne gagner, sauf leurs complices.
Ces trois cartes ou trois dés, selon la théorie des probabilités, sont les gagnants pour les organisateurs du jeu, et puis il y a le tour de passe-passe.
Il n'y a pas de tour de passe-passe ou de théorie de l'improbabilité. :) C'est tout à fait banal et simple. Je le sais de première main. C'était dans les années 1990 et le système m'a été décrit en détail par un homme qui y était lui-même impliqué. Aujourd'hui, les gens ne sont plus dupes ; les escrocs opèrent principalement en ligne. Mais les principes de base restent les mêmes. Attirer une personne, profiter de ses faiblesses et lui soutirer de l'argent, et ensuite, sous n'importe quel prétexte, l'argent n'est jamais rendu.
Les conditions du jeu ne sont pas entièrement décrites, comme d'habitude.
Est-il possible de gagner plus que sa mise ? Sinon, il n'y a aucun intérêt à jouer.
Alors il devrait être autorisé à gagner sur le pot. Il suffit donc de faire la mise minimale, il y aura un gain.
Peut-être que la condition est que vous pouvez jouer une fois, et ici nous devons décider de la mise, afin qu'il y ait la probabilité maximale de gagner.
Comme tous les "pradlocks" - à partir de conditions incomplètes.
Solution :
Il n'est même pas question de parier. Pari 1. Cela n'a plus de sens, la probabilité de gagner ne dépend pas de la taille de la mise. Donc 1, juste pour commencer le jeu.
Alors, quel est le paradoxe ? En partant du principe qu'il faut miser plus pour augmenter ses gains ? C'est peut-être ça.
Le principe du jeu : pour entrer dans le jeu, un dépôt est nécessaire et le jeu de pièces dure jusqu'à ce que le premier aigle apparaisse (jeu unique), 1-doucat gagne lorsqu'un aigle apparaît au premier lancer, s'il y a eu pile et qu'un aigle apparaît au deuxième lancer, le montant du gain est doublé, et ainsi de suite à l'infini, jusqu'à ce qu'un aigle apparaisse. Probabilité de gagner 1 ducat-0.5, 2-0.25, 4-0.125 etc., donc vous pouvez gagner infiniment, et jouer infiniment, si le pot est infini.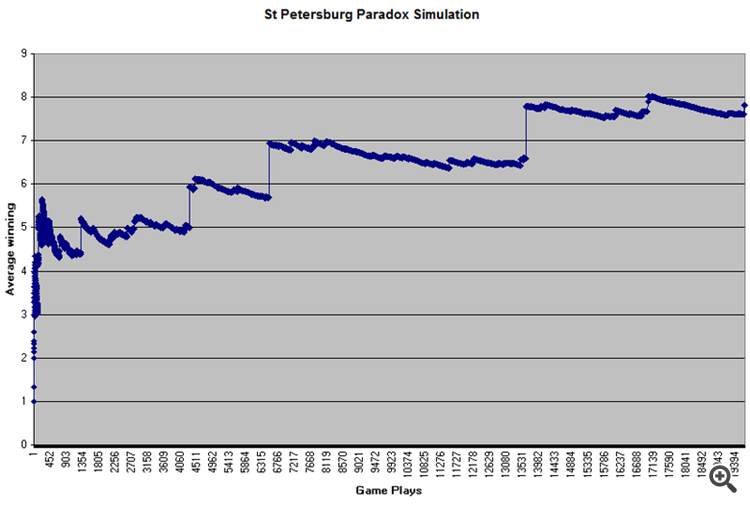
il s'agit d'une fonction non linéaire.
y=2^x.
et où tend Y dans une fonction non linéaire si X tend vers l'infini ? exact, vers l'infini.
Par conséquent, si le nombre de parties = infini, alors le gain moyen = infini.
Et le problème est également réglé de telle sorte que ses pertes sont une fonction linéaire (toujours 25 roubles chacune), et ses gains une fonction non linéaire.
Vous devez tracer deux fonctions. Le premier graphique sera d'abord plus élevé que le second, puis ils échangeront leurs places.
Tout dépend du nombre de jeux.
Exactement.
Mais que faire si nous avons besoin de 0 à 5, ou à 7 ou à tout autre nombre ? Nous devons encore le diviser par 32768.0. Ou bien, existe-t-il des variantes ?
1) Si vous n'êtes pas satisfait de la qualité du CRT (par exemple, avec des bits faibles), vous devez le faire passer par AES.
Le reste de la division peut être pris, mais seulement s'il est divisé par des puissances de 2. Sinon, quelle que soit la qualité du GSF, le résultat ne ressemblera en rien à une distribution uniforme.
3) Avec la division par deux, les comparaisons peuvent vraiment être faussées :-) Dans la plupart des cas, vous obtenez un résultat faible, mais faussé.
pour obtenir un numéro aléatoire de 0 à 6 (un parmi 7) :
- consider limit=RAND_MAX - (RAND_MAX%7) ; le multiple maximal de 7 dans l'intervalle 0..RAND_MAX
- utiliser RDS jusqu'à ce que nous obtenions r<limite ; c'est-à-dire que si le "nombre aléatoire" est supérieur à la limite, nous ne pouvons rien en faire - nous prenons
- résultat = r % 7 ou (pour le meilleur ou le pire) r * 7 / limite
en quelque sorte :-) peut se tromper +-1,