Bonjour à tous...
J'ai une question sur la transformée de Fourier...
Après une transformation de Fourier et un filtrage passe-haut avec transformation inverse,
Je dois continuer à calculer la fonction résultante en dehors de la plage de la transformation (si vous pouvez donner un exemple)...
Rien d'autre ne doit être calculé, car la transformée de Fourier ne s'applique effectivement qu'aux fonctions périodiques.
Supposons que nous ayons un signal périodique sur la plage obtenue,
la conséquence est que le début du tableau est une continuation de la séquence périodique... N'est-ce pas ?
Supposons que nous ayons un signal périodique sur la plage obtenue,
la conséquence est que le début du tableau est une continuation de la séquence périodique... >> n'est-ce pas ?
Quel genre de tableau ?
La transformée de Fourier est effectuée sur la période approximative de 0 à 2 * PI.
2*PI est de 0 degré pour la période suivante pour laquelle l'approximation a déjà été effectuée sur la période précédente.
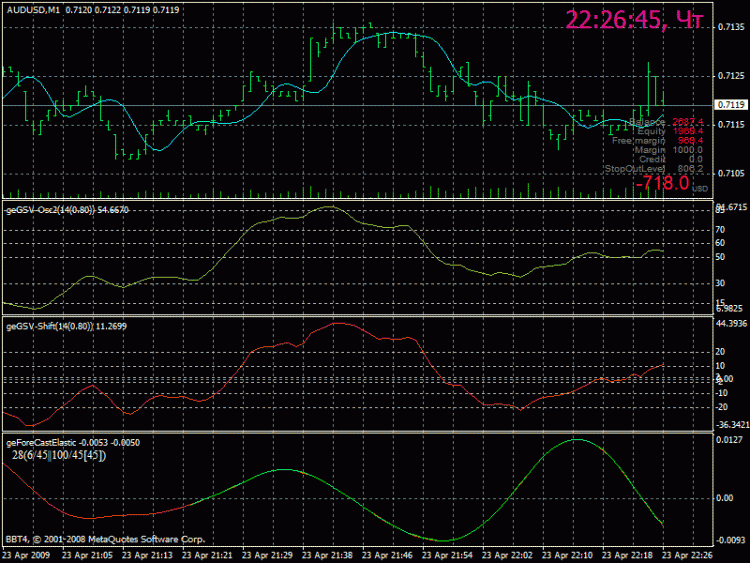
Alors regardons la figure...
La courbe (rouge) dans l'affichage inférieur est la ligne verte obtenue dans le processus de conversion avec les paramètres suivants
la taille de la fenêtre de conversion 2^6=64 points, le nombre de fréquences utilisées est de 45.
c'est-à-dire que nous obtenons un semblant de la courbe résultante ... qui a été superposée à l'original ...
comme vous pouvez le voir sur la figure, substituer le début à la fin n'est pas un vrai résultat -
La question est donc de savoir comment poursuivre la courbe comme indiqué par la ligne verte...
....
La question est donc de savoir comment poursuivre le mouvement de la courbe représentée par la ligne verte...
C'est le truc avec Fourier et les transformations similaires !
Il faut d'abord ramener la non-stationnarité du marché à une forme quasi-stationnaire, au moins...
Ensuite, vous pouvez tout transformer en ondes sinusoïdales stationnaires et continuer où vous voulez. Mais... Vous n'irez probablement nulle part...
Peut-être devrions-nous poser la question d'une manière différente alors...
De quelle manière la fonction représentée sur la figure peut-elle être approchée de manière à ce que la courbe puisse être poursuivie dans une petite section ?
Peut-être devrions-nous poser la question d'une manière différente alors...
Quelle est la meilleure façon d'approximer la fonction illustrée dans la figure de façon à ce que la courbe puisse être poursuivie dans une petite zone ?
Dans une petite zone, toute méthode d'approximation peut être utilisée, en l'utilisant pour extrapoler.
J'utilise le Lagrangien.
Alors regardons la figure...
La courbe (rouge) dans l'affichage inférieur est la ligne verte obtenue dans le processus de conversion avec les paramètres suivants
la taille de la fenêtre de conversion 2^6=64 points, le nombre de fréquences utilisées est de 45.
c'est-à-dire que nous obtenons un semblant de la courbe résultante ... que nous avons imposée à l'original ...
comme vous pouvez le voir sur la figure, substituer le début à la fin n'est pas un vrai résultat -
La question est donc de savoir comment poursuivre le mouvement de la courbe représentée par la ligne verte...
1. Pourquoi diable avez-vous décidé que les 64 points pris pour l'approximation sont une fonction périodique ?
2. Le nombre d'harmoniques ne peut pas dépasser la moitié des échantillons prélevés, c'est-à-dire que si l'approximation est faite par 64 divisions de la période, l'harmonique maximale sera la 31e.
3. résultat irréaliste car vous avez pris une fonction non périodique pour l'approximation et donc la continuation de la période ne correspondra pas. On vous a déjà dit que l'IP n'est efficace que sur les fonctions périodiques, tout le reste n'est qu'un jeu de tambourin.
Vous devez prendre deux périodes identiques : 0 - 2*PI, 2*PI - 4*PI. Utilisez les deux pour générer des PF et comparez s'il y a une correspondance dans les amplitudes et les phases des harmoniques. Si ce n'est pas le cas, cela signifie que la fonction n'est pas périodique et que la période d'échantillonnage doit être augmentée ou diminuée (diminution ou augmentation - il s'agit d'examiner les déphasages pour les harmoniques individuels).
Tout le reste n'est que danse avec tambourin.
Il est nécessaire de prendre deux périodes identiques : 0 - 2*PI, 2*PI - 4*PI. Pour les deux, il est nécessaire de plier le PF et de comparer s'il y a une correspondance dans les amplitudes et les phases des harmoniques. Si non, cela signifie que la fonction n'est pas périodique et que la période d'échantillonnage doit être augmentée ou diminuée (la diminution ou l'augmentation dépend des déphasages des harmoniques individuels).
En principe, il s'agit également de la "danse du tambourin", mais avec plus d'"artifices". Le résultat sera une histoire plus "jolie", rien de plus.
Périodique est une fonction pour laquelle il existe T tel que pour tout x l'égalité suivante f(x) = f(x+T) est vraie. Alors T est la période de la fonction f(x).
En d'autres termes, le trader n'a aucune garantie que lorsque T est choisi selon l'algorithme suggéré (comme un multiple commun de deux périodes consécutives), la troisième période de la même taille d'échantillon correspondra à la valeur sélectionnée (et la troisième est juste la période pour laquelle l'extrapolation est faite). Il n'y a aucune garantie avec aucun algorithme pour choisir T.
Et d'ailleurs - si la fonction est périodique - pourquoi avons-nous besoin de ce Fourier ? Personne n'y a jamais pensé ? Trouvez un point et remplacez les valeurs, c'est tout ;). C'est, bien sûr, si vous avez trouvé la période et n'avez pas dansé avec le tambourin....
>> Bonne chance avec ça.
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
Bonjour à tous...
J'ai une question sur la transformée de Fourier...
Après une transformation de Fourier et un filtrage passe-haut avec transformation inverse,
vous voulez continuer à calculer la fonction résultante en dehors du domaine de la transformée (si vous pouvez donner un exemple)...