Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Non, ce n'est pas ça. D'après cette formule, il apparaît que le GVH est corrélé. Tout le temps, r est autour de moins 0,5.
Voici le code de test.
Je l'ai vérifié.
Sergei, faisons un pas à la fois.
1. Nous travaillons avec un BP similaire à un devis. Une telle série est obtenue en intégrant CB avec un MO nul. Exemple de CB avec zéro MO :
dX=rnorm(n+1,0,10), où n+1 est le nombre de membres de la CB ayant une distribution gaussienne, 0 est MO égal à zéro dans mon cas et 10 dans votre exemple, 10 est la largeur de cette distribution dans mon cas et 100 dans le vôtre. Pour construire une BP similaire à celle du prix, nous devons intégrer la série initiale (trouver sa somme commutative) :
Voici à quoi ressemble la distribution des incréments de la BC intégrée (Fig. de gauche) et les incréments eux-mêmes sur le fond de la BC (lignes rouges et bleues sur la Fig. de droite) :
Sergey, nous étudions les propriétés de BP (la bleue), alors que dans votre post, vous avez substitué la toute première différence (dX dans ma notation et X dans la vôtre) dans la formule pour calculer le coefficient de corrélation de la première différence de la série. Bien sûr, vous obtiendrez R=0,5 et il ne devrait pas y en avoir d'autre (c'est prouvé élémentaire). Ainsi, si vous calculez maintenant par la formule que je propose r pour le CB intégré avec zéro MO (le bleu dans la figure de droite), vous obtiendrez le zéro attendu :
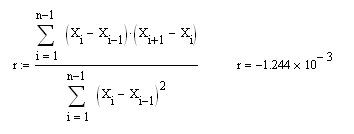
Et, bien sûr, c'est la même chose que r pour une série de dX incréments (mais, par une formule différente) :
J'espère que nous avons maintenant un consensus sur ce point ?
P.S. Vous pourriez le faire de cette façon :
Très bien, allons-y dans l'ordre.
J'ai fait ce que vous avez dit, j'ai réintégré la CB avec MOJ=0. Voici tout le code.
Cela semble correct à première vue. Mais il y a un piège. Alimentons un tableau corrélé à l'entrée de la formule. Comme tendance + bruit. y=a*x+b+rnorm(). Cela peut être fait simplement en mettant 0,5 au lieu de MOJ=0.
Sur la figure, vous pouvez voir que la courbe (bleue) est clairement corrélée. Après l'avoir divisé en deux tableaux A et B, calculons le coefficient de corrélation, il s'avère être de 0,993. Selon votre formule, elle est de 0,225.
Le problème est que, par définition, le coefficient de corrélation (CC) est compté entre les deux tableaux. Vous utilisez le même. Vous pouvez le faire en comparant un tableau à lui-même. C'est ce qu'on appelle l'ACF, c'est-à-dire qu'on forme deux tableaux A - initial, et le second B décalé dans le temps par rapport à A, et on construit un graphique - la dépendance du coefficient de corrélation par rapport au décalage. S'il n'y a pas de décalage, l'ACF est bien sûr égal à 1. Voici le tracé ACF de la dernière courbe bleue.
C'est l'approximation. Donc, je reste sur mon opinion que vous calculez par cette formule, mais ce n'est pas AC. Les chiffres ne s'additionnent pas.
Mais nous sommes allés de travers. Nous devons d'abord calculer correctement le Hurst et ensuite voir comment il diffère du QC.
Voici un article intéressant qui analyse différentes séries chronologiques.
en utilisant l'indice Hearst.
La figure montre que la courbe (bleue) est clairement corrélée. En le divisant en deux tableaux A et B, nous trouvons le coefficient de corrélation, qui est de 0,993. Votre formule nous donne 0,225.
Ici, je ne comprends pas tout.
Dans quels tableaux avez-vous divisé le BP de tendance ? Dans une droite Y=a*X+b et une composante aléatoire avec zéro MO, et entre elles vous cherchez le coefficient de corrélation ?
Voici un article intéressant qui analyse diverses séries chronologiques.
en utilisant l'index de Hearst.
Je n'ai pas tout compris ici.
Je comprends maintenant.
Vous recherchez le coefficient de corrélation entre la PA d'origine (pas ses incréments) et la même PA, mais décalée de 500 comptes vers la droite. C'est-à-dire que vous cherchez le coefficient de corrélation entre deux BP toujours positifs ! Bien sûr, il sera toujours positif et très grand (environ 1).
Sergey, je ne te comprends pas ! Que comptez-vous, le coefficient de corrélation entre la TA initiale et la même mais décalée ? Pourquoi diable en avons-nous besoin ? Nous nous intéressons au coefficient de corrélation entre des échantillons voisins dans la série de la première différence du BP initial. C'est ce coefficient qui montre la dépendance de l'incrément attendu par rapport aux incréments précédents. C'est ce coefficient qui est identique au Hurst décalé de 1/2.
>> Merci. >> Voyons voir.
Il semble y avoir une certaine véritéici.
J'ai essayé de le mettre en œuvre, mais j'ai été très proche de 1 pour les taux.
______________
J'ai relu l'article. Je crois que je suis du mauvais côté de la médaille.
Pour les paires de devises, l'indice de Hearst devrait être calculé pour le dérivé, je l'ai calculé pour le taux de change.
J'ai relu l'article... j'ai en quelque sorte marché sur un râteau.
Ouais :-)
Je m'avance un peu.
Voici comment se présente la série du taux intégré du SV et de l'EURGBP (Fig. de gauche), et voici comment se présentent les amplitudes de leurs incréments sur différents TF en double échelle logarithmique (Fig. de droite), sur l'axe des abscisses est tracé le logarithme du TF :
Hers, affirme que la tangente de l'angle de pente de ces lignes est égale à 1/2 pour une variable aléatoire intégrée (il est insensé de trader sur un tel quotient), inférieure à 1/2 pour un marché en pullback et supérieure à 1/2 pour un marché en tendance. Voyons ce que cet angle représente pour le NE. Ici, nous pouvons, comme conseillé dans l'article, tracer une ligne ISC et trouver sa pente, mais je vais trouver cette valeur localement - en traçant une ligne passant par tous les deux points. Le résultat sera un PC pour chaque TF :
Les cercles représentent ici le PC pour le CB (rouge) et le bleu pour le quotient EURGBP sur l'axe des abscisses pour le TF en min. Les croix montrent le coefficient de corrélation entre les lectures voisines pour la première différence de la série originale avec un décalage de 1/2. Le coefficient de corrélation a été calculé selon la formule donnée dans le premier message de cette page. On peut constater que la concordance entre ces deux façons d'estimer la prévisibilité de la PB est satisfaisante, alors que les formules dans mon cas sont beaucoup plus petites (une seule). Ce qui est, en fait, ce qu'il fallait montrer.
De plus, la série aléatoire a donné PX=1/2 et r=0 (il y a un biais dans la figure) comme le montre la définition. Pour le quotient, une tendance à l'évolution (antipersistance) est clairement visible, plus le TF est grand, plus il est petit.
Nous montrons ici le PCB pour le CB (rouge) et en bleu pour le kotier EURGBP ; sur l'axe des abscisses, le TF est tracé en min.
La série aléatoire a donné PX=1/2 et r=0 (il y a un biais dans la figure) comme le montre la définition. Pour le cotier, nous pouvons clairement voir une tendance au pullback (antipersistance), plus le TF est grand, plus il est petit.
C'est probablement la raison pour laquelle les pips sont si friands de l'euro-livre.
J'imagine que c'est pour ça que les pipsmen aiment tant l'euro-livre.
C'est évident !
C'est évident !
Par pure curiosité - j'aimerais trouver des paires extrêmement persistantes,
ou du moins les conditions dans lesquelles la persistance se produit) :