Maths pures, physique, logique (braingames.ru) : jeux cérébraux non liés au commerce - page 125
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Il semble correspondre à toutes les options en 2 pesées
ce dessin est quelque chose d'étranger...
Bizarre, je pensais que c'était plus clair, je pense que l'image est plus illustrative que les mots. OK, quelques commentaires :
Pour la première pesée, nous mettons deux boules sur chaque godet de la balance, de sorte que dans chaque godet nous avons une boule de la couleur choisie et une boule d'une autre couleur différente des couleurs des boules dans le panier opposé. (Sur l'image, il s'agit d'une balle rouge avec une balle verte et d'une balle rouge avec une balle bleue). Les résultats de la première pesée peuvent être différents : option 1.1) la balance est équilibrée et option 2) la balance est déséquilibrée, l'un des gobelets l'emporte sur 2.1). C'est-à-dire que nous avons deux branches de la solution.
Dans la première variante, on divise les boules en deux groupes homogènes (groupe ' et groupe '), puis 1.2) on pèse simplement les deux groupes (3 boules par tasse de la balance) et on détermine lequel est le plus lourd. Ça y est, les balles lourdes sont trouvées.
La deuxième option peut se produire dans deux cas (généralisés). Lorsque les deux boules de couleur de la première pesée dans chaque gobelet sont soit lourdes, soit légères. Par (2.2) après avoir marqué les boules en groupes (groupe ' et groupe ') nous déterminons par une seule pesée avec une boule lourde, lequel des groupes appartient au groupe lourd et lequel au groupe léger.
Voici une photo de l'internet....
OK, quelques commentaires :
Maintenant, le schéma est clair.
La deuxième option peut se produire dans deux cas (généralisés). Lorsque les deux boules de couleur de la première pesée dans chaque gobelet sont soit lourdes, soit légères.
Bizarre, je pensais que c'était plus clair, je pense que l'image est plus illustrative que les mots. OK, quelques commentaires :
Pour la première pesée, nous mettons deux boules sur chaque godet de la balance, de sorte que dans chaque godet nous avons une boule de la couleur choisie et une boule d'une autre couleur différente des couleurs des boules dans le panier opposé. (Sur l'image, il s'agit d'une balle rouge avec une balle verte et d'une balle rouge avec une balle bleue). Les résultats de la première pesée peuvent être différents : option 1.1) la balance est équilibrée et option 2) la balance est déséquilibrée, l'un des gobelets l'emporte sur 2.1). C'est-à-dire que nous avons deux branches de la solution.
Dans la première variante, on divise les boules en deux groupes homogènes (groupe ' et groupe '), puis 1.2) on pèse simplement les deux groupes (3 boules par tasse de la balance) et on détermine lequel est le plus lourd. Ça y est, les balles lourdes sont trouvées.
La deuxième option peut se produire dans deux cas (généralisés). Lorsque les deux boules de couleur de la première pesée dans chaque gobelet sont soit lourdes, soit légères. Par (2.2) nous déterminons avec une seule pesée (groupe ' et groupe '), lequel est le lourd et lequel est le léger.
Gardez vos doutes pour vous. CensuréSans vouloir vous offenser...
Option 1.1 que j'ai suggérée en privé. le début est faux.
Merci pour les félicitations, les gars, mais la vérité passe avant tout !
En bref : deux ou trois ?
Si c'est deux, donnez-moi un diagramme, car je connais moi-même pour trois.
Bien merci, alors la deuxième branche de la solution diverge en trois options (l'option c est ajoutée)
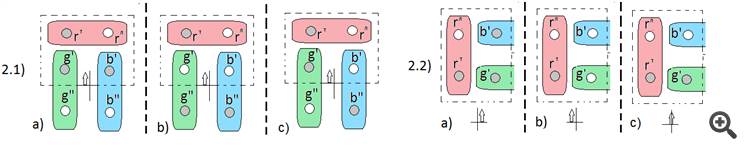
Et la deuxième pesée sera organisée à partir des mêmes boules que la première, mais dans une disposition différente. Par conséquent, après la deuxième pesée, nous aurons l'une des trois réponses, grâce à laquelle nous pourrons reconstituer la position des boules lors de la première pesée, et connaissant la boule lourde de la première pesée (la verte lourde), nous pourrons déterminer le poids des autres.Andrei, quelle est votre solution pour les trois boules (la mise en page initiale pour chaque pesée suffit) ?
Selon certains, il existe plusieurs solutions.
Andrei, quelle est votre solution pour trois boules (la mise en page initiale pour chaque pesée suffit) ?
Je n'ai pas d'option :) la solution ci-dessus semble être correcte.
______________
Et bon anniversaire :) Plus de problèmes de puzzle intéressants pour vous et pour les résoudre tous.
Je n'ai pas le choix :) la solution ci-dessus semble être la bonne.
______________
Et bon anniversaire :) Je vous souhaite de nombreux problèmes de puzzle intéressants et que vous les résolviez tous.
Merci, Andrew.
J'ai peur de devoir poster plus souvent ceux que je n'ai pas résolus. Mais résolvez-les de toute urgence (je n'aime pas lire les solutions des autres si je ne les ai pas résolues moi-même) !
P.S. Avez-vous résolu le problème du 53 ?