Maths pures, physique, logique (braingames.ru) : jeux cérébraux non liés au commerce - page 150
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
(4) Découpez le carré en un nombre minimum de triangles à angles vifs.
Explication : Aucune justification n'est nécessaire.
(4) Pour la Journée du méga-cerveau, des t-shirts nominatifs ont été distribués, strictement un par personne. Les mégabres étaient censés entrer dans la pièce un par un dans un certain ordre, trouver leur T-shirt, l'enfiler et partir. Mais malheureusement, le premier méga-cerveau a cessé de fonctionner et a été remplacé par un mini-cerveau, qui n'a pas eu le temps de se procurer son propre T-shirt. La procédure reste la même, mais le mini-cerveau entre le premier dans la pièce et enfile tout T-shirt qu'il trouve. Ensuite, chaque mégabrain, s'il ne trouve pas son propre T-shirt, met n'importe lequel des autres. Quelle est la probabilité que la dernière personne à entrer dans la pièce mette son T-shirt ?
Ay mala !
Vous n'écrirez pas de justification, parce que c'est évident ?
Ay mala !
Vous n'écrirez pas de justification, parce que c'est évident ?
Ce n'est pas très évident, mais c'est trop ennuyeux à écrire. Ce n'est pas facile là-bas, ce n'est pas facile...
;)
(4) Découpez le carré en un nombre minimum de triangles à angles vifs.
Explication : Aucune justification n'est nécessaire.
Rien de moins n'est possible.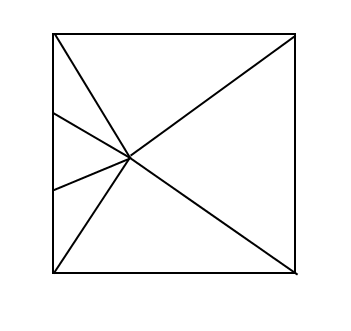
Nisachod. Deux angles obtus. Ceux qui sont à gauche, aux coins du carré.
Va. C'est vrai.
Alors ce n'est pas bon, pas de solutions simples du tout.
J'en ai au moins 14 jusqu'à présent. Qui en a le moins ?
10. Si vous le défendez.
Un bon fumeur ! Je ne m'attendais pas à ce que ce soit tellement mieux. Je vais continuer à penser.
Pouvez-vous diviser un triangle rectangle en moins de 5 triangles à angle vif ?