L'Apprentissage Automatique dans le trading : théorie, modèles, pratique et trading algo - page 436
Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Ça marche, merci ! Intéressant comment ça marche...
Recherche-t-il l'option la plus similaire ou fait-il une moyenne sur plusieurs ? Apparemment, il trouve le meilleur. Je pense que je devrais opter pour 10 ou même 100 variantes et rechercher la prédiction moyenne (le nombre exact devrait être déterminé par l'optimiseur).
Oui, ici il montre 1 meilleur, je ne me suis pas embêté avec beaucoup de variantes, vous pouvez essayer de refaire si vous comprenez mon écriture ;)
Je n'ai jamais été capable d'apprendre à faire des transactions rentables en utilisant uniquement les prix. Mais le modèle de patron l'a fait, donc le choix est évident :)
C'est une chose de trouver un "modèle", mais c'en est une autre de lui donner un avantage statistique. IMHO, j'en doute beaucoup pour une raison quelconque. En fait, la recherche de modèles par convolution (produit, différence) sur toute la longueur d'une série historique avec moyennage revient à faire une régression en NS avec UN NEURON, c'est-à-dire le modèle linéaire le plus simple avec des signes extrêmement stupides, une tranche de prix telle quelle.
C'est une chose de trouver un "modèle", mais c'en est une autre de trouver un avantage statistique. IMHO, j'en doute fort. En fait la recherche de patterns par convolution (produit, différence) sur toute la longueur des séries historiques avec moyennage, c'est comme faire de la régression en NS avec UN NEURON, c'est à dire le modèle linéaire le plus simple, avec des signes extrêmement émoussés, une tranche de prix telle quelle.
S'il s'agit d'un seul neurone, alors avec un nombre d'entrées égal à la longueur du motif, (motif de 30 barres = 30 entrées NSb de 500 barres = 500 entrées NS).
À mon avis, de nombreux neurones dans les couches internes du SN sont analogues à la mémoire, 10 - 50 - 100 neurones supplémentaires sont correspondants à 10 - 50 - 100 variantes mémorisées des signaux d'entrée. Et en comparant le modèle avec 375 000 variantes de l'histoire (M1 pendant un an), nous avons une mémoire absolument précise et complète, au lieu des 10 -50 - 100 variantes les plus fréquemment rencontrées. Ensuite, à partir de cette mémoire, le chercheur de motifs identifie les N résultats les plus similaires et obtient la prédiction moyenne, tandis que le réseau neuronal augmente le poids des connexions entre les neurones pour chaque motif similaire.
La raison pour laquelle la convolution doit être appliquée n'est pas claire, je suppose que vous proposez de convoluer le motif recherché avec chaque variante de l'historique, comme résultat nous obtenons la 3ème séquence temporelle - et comment cela aide-t-il à déterminer la similarité du motif et de la variante vérifiée ?S'il s'agit d'un neurone, alors avec un nombre d'entrées égal à la longueur du modèle, (modèle de 30 barres = 30 entrées NS de 500 barres = 500 entrées NS).
Une autre chose qui n'est pas claire est la raison pour laquelle la convolution doit être appliquée, je suppose que vous proposez de convoluer le motif recherché avec chaque variante de l'historique, comme résultat nous obtenons la 3ème séquence temporelle - et comment cela aide à définir la similarité du motif et de la variante testée ?
Oui, c'est la version 1 qui est la meilleure ici, je ne me suis pas embêté avec de nombreuses variantes, vous pouvez essayer de la refaire si vous comprenez mon écriture ;)
en regardant la photo, quelque chose ne va pas...
Voici un exemple au hasard
Votre ligne de prévision bleue va très fortement vers le bas, avec un faible mouvement d'une variante similaire...
Voici juste photoshopé cette variante et il s'est avéré pas si raide et plus logique par idée.
pendant que je regarde l'image, quelque chose ne va pas...
Voici un exemple au hasard
Votre ligne de prévision bleue descend très abruptement, avec un faible mouvement d'une variante similaire...
Voici juste photoshopé cette variante et il s'est avéré pas si raide et plus logique par idée.
J'ai remarqué :) dans certaines situations, il ne compte pas l'angle correctement pour une raison quelconque, cela a commencé lorsque j'ai réécrit la version d'une seule image temporelle à une version multi-image temporelle, et je n'ai toujours pas trouvé où est le problème.
D'ailleurs, il est possible que je n'aie pas du tout compté correctement... je n'ai pas pensé à vérifier avec photoshop. L'angle entre les graphiques précédents et les prévisions devrait être le même
Exactement.
Vous réduisez le modèle et la ligne où les extrêmes étaient les plus similaires, c'est simple. Par exemple, vous avez une ligne {0,0,0,1,2,3,1,1,1,1} et vous voulez y trouver un motif {1,2,3}, la convolution vous donnera {0,0,0,3,8,14,11,8, 6} (compté à l'œil) 14 au maximum où se trouve la "tête" de notre motif. Bien sûr, il est souhaitable de normaliser les vecteurs avant la convolution, sinon il y aura des extrema aux endroits où les nombres sont importants.
Pourquoi compliquer les choses comme ça ? Pourquoi devrions-nous chercher un extremum sur la convolution si nous pouvons chercher {0,0,0,1,2,3,1,1,1} spécifiquement dans la ligne {1,2,3} ? En dehors de l'augmentation de la complexité et du temps de calcul, je ne vois aucun avantage.
Pourquoi compliquer les choses comme ça ? Pourquoi devrions-nous chercher un extremum sur la convolution si nous pouvons chercher {0,0,0,1,2,3,1,1,1} spécifiquement dans la série {1,2,3} ? En dehors de la complication et du temps de calcul plus long, je ne vois pas d'avantages.
Hmmm... qu'entendez-vous par "recherche spécifique" ? Veuillez me donner un exemple d'algorithme plus rapide que la convolution.
Deux opérations peuvent être utilisées : la différence de longueur de vecteur et le produit scalaire, la différence de longueur, croyez-moi est 3-10 fois plus lente, la différence de composante, l'élévation au carré, la somme, l'extraction de racine, et la convolution est de multiplier et d'ajouter.
Il faut prendre chaque morceau d'une ligne de longueur 3 comme un vecteur et le comparer pour la "similarité" à notre {1,2,3}.
Hmmm... qu'entendez-vous par "recherche spécifique" ? Veuillez me donner un exemple d'un algorithme plus rapide que la convolution.
La méthode la plus simple consiste à déplacer pas à pas la largeur de la fenêtre de l'exemple recherché dans la séquence et à trouver la somme des valeurs abs. des deltas :
0,0,0 et 1,2,3 erreur = (1-0)+(2-0)+(3-0)=6
0,0,1 et 1,2,3 erreur = (1-0)+(2-0)+(3-1)=5
0,1,2 et 1,2,3 erreur = (1-0)+(2-1)+(3-2)=3
1,2,3 et 1,2,3 erreur = (1-1)+(2-2)+(3-3)=0
2,3,1 et 1,2,3 erreur = (2-1)+(3-2)+Abs(1-3) =4
Où l'erreur minimale correspond à la similarité maximale.
Remarqué :) dans certaines situations, il ne compte pas l'angle correctement pour une raison quelconque, cela a commencé après que j'ai réécrit à partir d'une version à une seule image temporelle à une version à plusieurs images temporelles, et je n'ai jamais attrapé où le défaut se trouve.
Au fait, il est possible que je n'ai pas du tout compté correctement... Je n'ai pas réussi à le vérifier avec Photoshop. Je devrais obtenir le même angle entre les graphiques précédents et les prévisions.
Je ne suis pas encore sûr qu'il soit correct de considérer des graphiques comme similaires avec une si grande différence dans les angles de pente. En reprenant le même exemple :
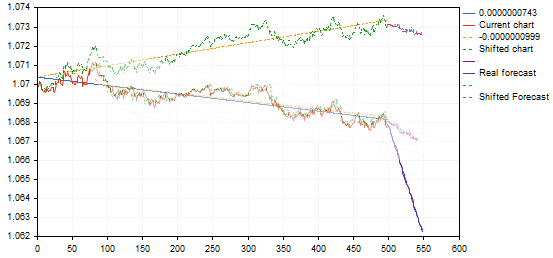
la variante trouvée donne un pullback à partir du point de tendance supérieur ou de la fin de la tendance, en la transférant sur le graphique de tendance, elle donnera une prévision pour une continuation de la tendance à la baisse, plutôt qu'un renversement - essentiellement un signal inverse. Quelque chose ne va pas ici.... peut-être n'avons-nous pas besoin de ces transformations affines.... ? Et une simple corrélation (erreur minimale) est suffisante ?