Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Oh, Dios mío. No pensé que fuera a suceder así)).
Oh, Dios mío. No pensé que fuera a suceder así)))
No. No creo en estos indicadores.
Mienten.
No te creas los indicadores. Confía en mí.
No. No confío en estos indicadores.
Mienten.
No te creas los indicadores. Confía en mí.
Eso no es lo que dijo Müller: No puedes confiar en nadie... Sí puedo.)
No es así como lo dice Müller: no se puede confiar en nadie... Sí puedo.)
Has conseguido hacerme reír por undécima vez hoy)). Diez veces al leer el siguiente hilo.
Pero sí que se puede confiar en mí. No soy Mueller))
Es el resultado de determinar la diferencia entre los extremos en función del cambio del valor del umbral de la ZZ de Kagi. Figura b)-curva acumulativa.
Lo mismo para la ZZ de Renko.
Observo una característica interesante: la distribución Chi-cuadrado:
Ver, en k=1, hay una similitud con la ZZ de Kagi, en k=2, exponente, exactamente igual que en el gráfico ZZ de Renko.
La distribución Chi-cuadrado tiende a la normalidad a medida que aumenta k.
Bueno, no sé...
La función es interesante, pero ¿cómo aprovecharla? Es difícil sugerir algo, dado que no soy bueno en Kagi o Renko de la palabra "en absoluto".
Pero, lo intentaré.
1. Hay que renunciar al deseo de conseguir una distribución normal y buscar durante siglos para encontrarla. Trabajar con los patrones ya encontrados es ya una cosa muy, muy grande.
2.https://en.wikipedia.org/wiki/Generalized_normal_distribution
3. En pocas palabras, xy-cuadrado con k=1 es la suma de los cuadrados de los NA con distribución normal, xy-cuadrado con k=2 es la suma de los NA con distribución de Laplace
4. Me interesaba el caso con k=2, porque los estudios demuestran que el mercado está dominado por la distribución de Laplace (doble geométrica para ser exactos)
5. No está claro aquí - en estos Renko lo que cuenta? ¿La suma de las diferencias (alto-bajo)?
6. Si es así - entonces la diferencia (High-Low) en Renko es SV que pertenece a la distribución de Laplace - debe ser confirmado experimentalmente.
7. A continuación, la suma de las diferencias (High-Low) en la ventana deslizante (para un determinado volumen de muestra) forma un cuadrado xy con k=2 con una función cuantil conocida
https://keisan.casio.com/exec/system/1180573197
8. Esperamos la salida (High-Low) en la ventana móvil más allá de los límites de un intervalo de confianza para un determinado cuantil y entramos en la operación.
Bueno, esto es sólo un esbozo del algoritmo, sólo para desarrollar el tema y nada más :)))
5. Aquí es donde no está claro - en estos Renko, ¿qué cuenta? ¿La suma de las diferencias (High-Low)?
7. A continuación, la suma de las diferencias (alto-bajo) en una ventana deslizante (para un determinado tamaño de muestra) forma un cuadrado xy con k=2 con una función cuantil conocida
https://keisan.casio.com/exec/system/1180573197
8. Esperar la salida (High-Low) en la ventana deslizante más allá de los límites del intervalo de confianza para un determinado cuantil y entrar en la operación.
5. Renko considera la ruptura a través del rango establecido por "Renko brick" en el valor de 1 "brick", además la ruptura debe ser en el valor de "brick", es decir, "brick" 10 puntos, para dibujar un nuevo Renko brick, el precio debe pasar por encima de la barra Renko ya formada 10п+1п (o por debajo en 10п+1п) y luego se dibujará un nuevo "brick". Es decir, en esencia, el precio está discretizado sin tiempo por el valor del "ladrillo Renko". Renko elimina los componentes de ruido del precio pero como cualquier filtro hay un desfase, para dibujar una nueva barra de Renko el precio debe pasar por 2 rangos = 2 alturas de ladrillo de Renko
7,8 es un indicador ATR, lo que escribes se suele llamar ruptura de volatilidad, pero hay un eterno problema - el periodo del ATR, si el periodo es pequeño, habrá ruido, si el periodo es largo, habrá retraso
Aquí
Foro sobre comercio, sistemas de comercio automatizados y prueba de estrategias de comercio
Pastores ZigZags
Novaja, 2018.08.26 23:22
Es el resultado de determinar la diferencia entre extremos en función del cambio del umbral de ZZ Kagi. Figura b)-curva acumulativa.
Lo mismo para Renko ZZ.
Observo una característica interesante: la distribución Chi-cuadrado:
Véase, en k=1, hay una similitud con la ZZ de Kagi, en k=2, exponente, exactamente igual que en el gráfico ZZ de Renko.
La distribución Chi-cuadrado tiende a la normalidad con el aumento de k.
Novaja habla de alguna diferencia entre los extremos... ¿Sobre el diferencial (High-Low) o algo así? No puedo entenderlo... Es demasiado seco y concisamente escrito...
Pero, parece un cuadrado xy - por eso estoy interesado. Encontrar patrones claros es muy raro.
No sé...
La función es interesante, pero ¿cómo se aprovecha? Es difícil sugerir algo, teniendo en cuenta que no soy bueno ni en el Kagi ni en el Renko de la palabra "en absoluto".
Pero, lo intentaré.
1. Hay que renunciar al deseo de conseguir una distribución normal y buscar durante siglos para encontrarla. Trabajar con los patrones ya encontrados es ya una cosa muy, muy grande.
2.https://en.wikipedia.org/wiki/Generalized_normal_distribution
3. En pocas palabras, xy-cuadrado con k=1 es la suma de los cuadrados de los NA con distribución normal, xy-cuadrado con k=2 es la suma de los NA con distribución de Laplace
4. Me interesaba el caso con k=2, porque los estudios demuestran que el mercado está dominado por la distribución de Laplace (doble geométrica para ser exactos)
5. No está claro aquí - en estos Renko lo que cuenta? ¿La suma de las diferencias (alto-bajo)?
6. Si es así - entonces la diferencia (High-Low) en Renko es SV que pertenece a la distribución de Laplace - debe ser confirmado experimentalmente.
7. A continuación, la suma de las diferencias (High-Low) en la ventana deslizante (para un determinado volumen de muestra) forma un cuadrado xy con k=2 con una función cuantil conocida
https://keisan.casio.com/exec/system/1180573197
8. Esperamos la salida (High-Low) en la ventana móvil más allá de los límites de un intervalo de confianza para un determinado cuantil y entramos en la operación.
Bueno, esto es sólo un algoritmo aproximado, sólo para desarrollar el tema y nada más :)Cgfcb,j
Muchas gracias, gran comentario.
Unas palabras sobre la construcción de la zz. La variante de Kagi.
El azul muestra el gráfico de ticks, el umbral es de 3p. Si el opuesto es mayor de 3 pips se dibuja un extremo, si no, vamos más allá. Es decir, las oscilaciones pueden contener 2,66; 3,66; n número de tales umbrales (segmentos) con valores fraccionarios. Este valor fraccionario se descarta en la construcción de tipo Renko, pero el principio es el mismo. Es decir, valores enteros 2,3, etc. Así vemos como los vértices fraccionados no se tienen en cuenta en la construcción. En la imagen de abajo hay una variante de Renko.
Ahora creo que la diferencia está clara. Así, la frecuencia de aparición de la relación entre la longitud de la oscilación y el valor umbral (segmento de 3p) para Kagi: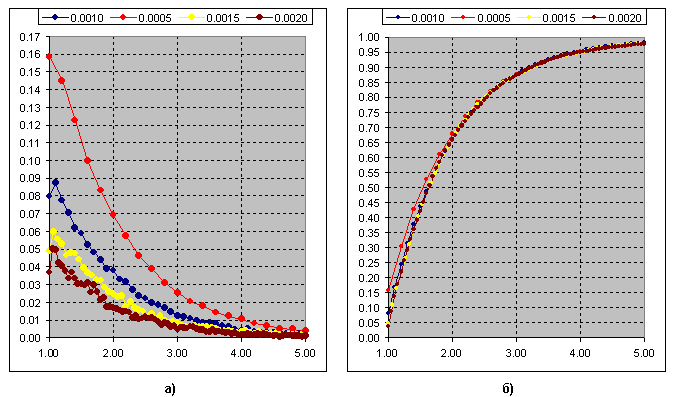
Fig.b) Suma acumulada de curvas. La distribución Chi-cuadrado en k=1 se ajusta a esta curva.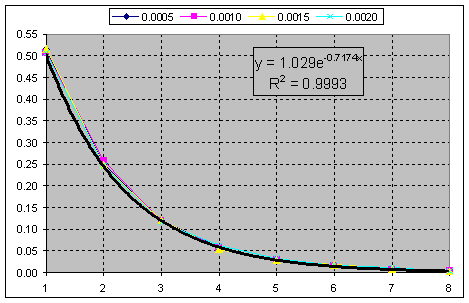
Y esta es la suma acumulativa de la frecuencia de ocurrencia del ratio de oscilación al umbral(segmento) para la construcción de Renko. Chi-cuadrado en k=2.
Es decir, sólo tenemos que descartar las partes fraccionarias y obtener un exponente puro.
Muchas gracias, gran comentario.
Unas palabras sobre la construcción de la zz. La variante de Kagi.
El azul muestra el gráfico de ticks, umbral - 3p. Si el opuesto es mayor de 3 pips se dibuja un extremo, si no, vamos más allá. Es decir, las oscilaciones pueden contener 2,66; 3,66; n número de tales umbrales (segmentos) con valores fraccionarios. Este valor fraccionario se descarta en la construcción de tipo Renko, pero el principio es el mismo. Es decir, valores enteros 2,3, etc. Así vemos cómo los vértices fraccionados no se tienen en cuenta en la construcción. En la imagen de abajo hay una variante de Renko.
Ahora creo que la diferencia está clara. Así, la frecuencia de aparición de la relación entre la longitud de la oscilación y el valor umbral (segmento de 3p) para Kagi:
Fig.b) Suma acumulada de curvas. La distribución Chi-cuadrado en k=1 se ajusta a esta curva.
Y esta es la suma acumulativa de la frecuencia de ocurrencia del ratio de oscilación al umbral(segmento) para la construcción de Renko. Chi-cuadrado en k=2.
Es decir, basta con descartar las partes fraccionarias para obtener un exponente puro.
Columpios... Eh-mah... :)))
BIEN. No voy a profundizar en la terminología. No hay tiempo.
Tenemos el exponente más puro de todo.
La suma de estos componentes será una distribución binomial negativa (la distribución Erlang para la NE continua) de nuevo, subrayo, con del famoso dispersión. El límite es la distribución normal que se busca.