Estadística de la dependencia entre comillas (teoría de la información, correlación y otros métodos de selección de características) - página 15
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
La gente que tiene EViews no hace esas preguntas, je je.
¿Sería tan amable de enviarme, por privado o aquí, EViews, si es posible?
La gente que tiene EViews no hace esas preguntas, jejeje
Pues sí, es una pregunta tonta, estoy de acuerdo. Las garantías son las mismas que las del propio modelo.
¿Qué versión tienes? Dicen que el 5 está anticuado.
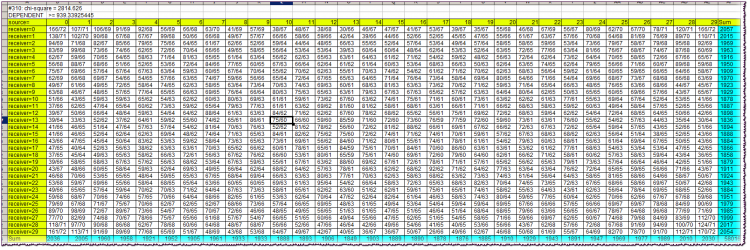
Primera línea del bloque: #310: chi-cuadrado = 2814,626Primero - el valor de la variable Lag. A continuación, el valor de chi-cuadrado de la independencia de las variables.
Segunda línea: conclusión de dependencia/independencia, junto con el valor límite de chi-cuadrado.
Las celdas amarillas de la tabla son tapas. Permiten orientar qué caracteres del alfabeto se observaron simultáneamente en la intersección de la fila y la columna correspondientes. Recordemos que los alfabetos de la fuente y del receptor son idénticos e iguales a los cuantiles en los que cayeron los rendimientos de las barras correspondientes (fuente y receptor).
Por ejemplo, en la intersección de la columna origen=10 y la fila receptor=13 encontramos un valor de celda de 75/60. Esto significa que la combinación "el retorno de la fuente (barra en el pasado) atrapado en el 10º cuantil y el retorno del receptor (barra más cercana al presente) atrapado en el 13º cuantil" se observó 75 veces en el historial, siendo el número teórico de tales combinaciones de 60 si fueran independientes.
Las celdas de color turquesa son las sumas de las frecuencias reales por fila o columna necesarias para calcular el chi-cuadrado.
El propio chi-cuadrado en el caso de la independencia de la fuente y el receptor debe ser casi siempre menor que el límite, es decir, especificado en la segunda línea del bloque. Como podemos ver, es mucho más grande, casi 3 veces mayor. Esto indica una fuerte dependencia de la barra en este caso.
Todo el archivo, incluso archivado, ocupa demasiado espacio, así que no puedo publicarlo aquí.
Pues sí, es una pregunta tonta, estoy de acuerdo. Las garantías son las mismas que las del propio modelo.
¿Qué versión está utilizando? Dicen que el 5 está anticuado.
Existe la definición de entropía de Shannon, en la que la independencia es obligatoria.
Y hay una definición de información mutua, en la que la definición de Shannon se aplica de manera puramente formal, ya que se sigue asumiendo que existen dependencias.
Si quiere ahondar en las profundidades filosóficas y las contradicciones de la definición de información mutua, por favor, hágalo. Prefiero no molestarme por ello y utilizar simplemente la fórmula "americana" con probabilidades, sin preocuparme por la independencia.
Un poco de nombre erróneo. La traducción de los significados de bark..., TI es la siguiente. Existe el concepto de entropía. Hay que entender claramente que detrás de esta hermosa e incomprensible palabra extranjera hay alguna figura inventada artificialmente. En los libros de texto, los más honestos, se escribe directamente así, una medida de incertidumbre introducida axiomáticamente. Lo que resulta es en realidad una convolución. A grandes rasgos, una gran tabla que describe los estados y sus frecuencias, con la ayuda de fórmulas aritméticas se conviertan en un número. Además, sólo se enrollan las frecuencias, y los propios estados (que, por cierto, también pueden tener sus medidas) sólo son interesantes desde el punto de vista de su número total.
En ter.faith hay una operación similar, a grandes rasgos, los sistemas de mo se cuentan de manera similar. Pero sólo ahí se multiplican las probabilidades de los estados con sus medidas, se suman y se obtiene una cifra, sobre la que luego se demuestran los teoremas sobre la convergencia, etc. Aquí no es así. En este caso, la propia frecuencia (llamada probabilidad), o más bien su logaritmo, actúa como medida. El logaritmo resuelve algunos problemas aritméticos que Shannon formuló en tres condiciones (debe crecer monótonamente, etc.).
Después de eso, Shannon dice: -Amigos, saben, he llegado a reglas razonables y obvias sobre cómo se pueden sumar los números que he descubierto recientemente, que llamo entropía, a partir de dos tabulaciones diferentes. Los amigos (en su mayoría militares) preguntan: - Bien, ¿cómo lo haces? - Muy sencillo. - Shannon les contesta, mostrando sus ojos. - Digamos que una placa no está conectada a otra, son independientes, eso pasa en la vida. Y en este caso tengo un teorema sobre la suma de entropías, con un resultado maravilloso: ¡los números simplemente se suman! - Bien, pero ¿y si las placas están conectadas de alguna manera incomprensible? - Aquí es igual de sencillo, construir una gran tabla cuadrada a partir de las dos tablas iniciales, multiplicar las probabilidades en cada celda. Sumamos los números en las celdas por columnas, sumamos las columnas por separado, construimos una nueva tabla, dividimos una por otra, aquí temprano cero, aquí pescado envuelto... ¡Uy, el resultado es un número, que yo llamo entropía condicional! Lo interesante es que la entropía condicional puede calcularse tanto de la primera tabla a la segunda, ¡y viceversa! Y para tener en cuenta esta desafortunada dualidad, he inventado la entropía mutua total, ¡y es la misma cifra! - Y así, - preguntan los amigos, masticando palomitas, - es mucho más fácil comparar una cifra con otra, que entender la esencia de los datos a partir de las tablas originales. Y es aún más fácil cuando se trata de entender los significados y la fiabilidad de las relaciones: es aburrido, de verdad. Cortina.
Esto es lo que me parece una breve historia de TI. Recopilado a partir de mis propias investigaciones y de las afirmaciones de un diccionario académico (véanse las citas anteriores).
Ahora, lo que es importante. El punto clave de toda esta historia se esconde en la entropía condicional. De hecho, si se quiere operar con una cifra, no es necesario contar ninguna información mutua y otras cosas, basta con dominar el método de cálculo de la entropía condicional. Es ella la que dará alguna medida de la interrelación de una con la otra. Por lo tanto, es necesario entender que las cifras en las tablas deben ser "estacionarias", y además, las interrelaciones de las tablas deben ser "estacionarias". Y además, las cifras iniciales de los cuadros deben proceder de fuentes adecuadas.
Hay que decir que existen extensiones de TI al caso de las cadenas de Markov. Parece ser justo lo que el doctor ordenó. Pero no, las probabilidades de transición del mercado no son constantes, debido a la no estacionalidad general. Además, mientras que para el CM no importa cómo acabó el sistema en su estado actual, para el mercado es muy importante.
No sé cuál es tu problema de alfabetización. Tengo un sistema de un par de barras separadas por la distancia Lag. Una barra, en el pasado, es la fuente y la otra es el receptor. Los alfabetos de ambos son idénticos (en lo que respecta a los retornos de barra, por supuesto).
Claramente, algo similar a la autocorrelación, pero con una medida diferente. Mis objeciones son exactamente las mismas que en el caso de CM. Y todos los demás, estacionarios, etc.
SZU. Debo decir que si realmente el comercio (TI) y con éxito, lo que con él, con las objeciones. Deja incluso un pie de liebre en el monitor, si ayuda.
Lee HideYourRichess.
Sí, interesante. En efecto, la matriz de frecuencias de los estados condicionales de un sistema -bajo el supuesto de la conectividad- al ser reformulada en términos de entropía condicional, nos da UNA cifra que describe la posibilidad de que exista cierta determinabilidad de una variable respecto a otra. Si la FDP de dicha matriz inicial es uniforme, entonces tenemos la máxima entropía del sistema (por supuesto, quise decir entropía condicional). Y si hay irregularidades, la entropía será menor. Como primera aproximación podemos hacerlo con una cifra. Tienes razón en eso. Y la información mutua para el conjunto de variables, separadas del receptor por Lag, como ha escrito Alexey, se calcula ya para fines bastante concretos, a saber, para la selección de variables informativas.
Hasta ahora, yo personalmente no comercio usando TI. Este tema fue un "primer intento", creo.
HideYourRichess: Вот так выглядит краткая история ТИ в моём исполнении. Составлена по мотивам моих собственных изысканий и утверждений академического словарика (см. цитаты ранее).
Muy interesante. Shannon hizo tal lío que aún estamos resolviendo...
Hay que decir que existen extensiones de TI para casos de cadenas de Markov. Parece ser justo lo que el doctor ordenó. Pero no, las probabilidades de transición del mercado no son constantes, debido a la no estacionalidad general. Además, si para CM no importa cómo quedó el sistema en el estado actual, para el mercado es muy importante.
Esa es la cuestión, el flujo de retorno no es un proceso markoviano, ya que el retorno de la barra cero depende fuertemente del retorno no sólo de la primera barra, sino también de la segunda, tercera, etc. En cualquier caso, así es como se puede interpretar directamente el estudio de la rama principal.
ZS. Tengo que decir que si realmente comercia con esto (TI) y con éxito, entonces qué demonios, con objeciones. Deja que la liebre pise el monitor, si eso ayuda.
No, no lo sé. Pero sería muy interesante convertirlo en algo comercial. He oído decir a alsu (Alexey ha desaparecido en alguna parte, lo siento), que recuerda vagamente un programa del canal RBC, en el que aparecía algún retórico-operador que realmente comercia algo parecido. Y apostó mucho dinero por ello. Y llama a su sistema "atrapar las ineficiencias del mercado".
Llevo mucho tiempo pensando en la entropía. Incluso puse algo aquí. Pero entonces era más bien entropía de física estadística, no de TI, y se refería a la multidivisa. De todos modos, el karma me ha estado susurrando algo entrópico al oído desde hace algunos años, y lo he estado escuchando y tratando de averiguar lo que quiere de mí...
Esa es la cuestión, el flujo de retorno no es un proceso markoviano, ya que el retorno de la barra cero depende fuertemente del retorno no sólo de la primera barra, sino también de la segunda, tercera, etc. En cualquier caso, así es como se puede interpretar directamente el estudio de la rama principal.
No, no comercio. Pero sería muy interesante desarrollar esto en algo comerciable. He oído decir a alsu (Alexey ha desaparecido en alguna parte, lo siento), que recuerda vagamente un programa en el canal RBC, en el que aparecía algún retórico-operador que realmente comercia algo parecido. Y apostó mucho dinero por ello. Y llama a su sistema "atrapar las ineficiencias del mercado".
Y hace tiempo que pienso en las entropías. E incluso publicó algo aquí. Pero entonces era más bien la entropía de la física estadística, no la de TI, y estaba relacionada con la multidivisa. De todos modos, el karma me ha estado susurrando algo entrópico al oído desde hace algunos años, y lo he estado escuchando y tratando de averiguar lo que quiere de mí...
Muy curioso.
Pero, Alexey, ¿podrías formular más claramente (en tu tabla) a qué hipótesis sobre la distribución de los rendimientos corresponden las estimaciones de chi-cuadrado?
¿El "browne" primigenio, o algo más fresco?
;)