Cálculo de diferencias, ejemplos. - página 6

Nuevo comentario
 

Promedio por polinomio de cuarto grado con apalancamiento 72 (EMA de cuarto grado) yextrapolación a diferentes apalancamientos mediante una parábola cúbica(polinomio de tercer grado).

      a1_Buffer[i]=((open[i] - Znach)    +5061600*a1_Buffer[i+1 ]-7489800    *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975;

      a5_Buffer[i+92]=a1_Buffer[i];   if(i<=1100) { for(z=92-1;z>=0;z--){        a5_Buffer[i+0+z]=  4*a5_Buffer[i+1+z]  -  6*a5_Buffer[i+2+z]  +  4*a5_Buffer[i+3+z]  - 1*a5_Buffer[i+4+z];  }}


      a2_Buffer[i+20]=a5_Buffer[i+20]; 
      
      a3_Buffer[i+38]=a5_Buffer[i+38]; 
      
      a4_Buffer[i+56]=a5_Buffer[i+56];
        
      a6_Buffer[i+74]=a5_Buffer[i+74];

La primera figura es un esquema de trazado, en la segunda figura todas las líneasque no se redibujan se dibujan hasta el último valor.

Los indicadores del sótano sólo se diferencian en el desfase de la línea establecida.


 

Promedio por polinomio de cuarto grado con apalancamiento 72 (EMA de cuarto grado) yextrapolación a diferentes apalancamientos utilizandoel polinomio de cuarto grado.

      a1_Buffer[i]=((open[i] - Znach)    +5061600*a1_Buffer[i+1 ]-7489800    *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975;

      a5_Buffer[i+92]=a1_Buffer[i];   if(i<=1100) { for(z=92-1;z>=0;z--){        a5_Buffer[i+0+z]=  5*a5_Buffer[i+1+z]  -  10*a5_Buffer[i+2+z]  +  10*a5_Buffer[i+3+z]  - 5*a5_Buffer[i+4+z]  +  1*a5_Buffer[i+5+z];  }}


      a2_Buffer[i+20]=a5_Buffer[i+20]; 
      
      a3_Buffer[i+38]=a5_Buffer[i+38]; 
      
      a4_Buffer[i+56]=a5_Buffer[i+56];
        
      a6_Buffer[i+74]=a5_Buffer[i+74];
  

La primera figura es un esquema de trazado, en la segunda figura todas las líneasque no se redibujan se dibujan hasta el último valor.

Los indicadores del sótano sólo se diferencian en el desfase de la línea establecida.


 

Alexei, puedo darte un consejo gratuito y una sugerencia.

Ya te he dicho que cambiar a la izquierda es, cómo decirlo suavemente... - una tarea ingrata. Sólo recibirás maldiciones de los que vean tu hilo. Por cierto, es una de las razones por las que te sientes orgulloso de estar solo en tu propio hilo.
Pero para desplazar una línea periódica con un punto de inflexión hacia la izquierda en una semionda (o más bien si sólo hay un punto de inflexión entre un mínimo y un máximo local) sin un desplazamiento real se puede utilizar la derivada de esa función. Es cierto que no es un cambio real, pero en esencia. La derivada de una función es el ángulo de una tangente a la recta. Calculado simplemente: buf[i]-buf[i+1].

Aquí están, por ejemplo, la primera y la segunda derivada de una onda sinusoidal. Los puntos de inflexión de la propia función se convierten en los máximos y mínimos locales de su derivada.

 
Nikolai Semko:

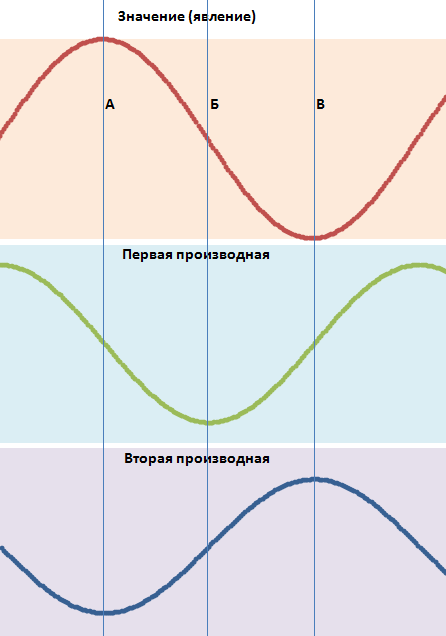
Alexey, puedo darte un consejo gratuito y una propina.

Ya he dicho que aplicar el cambio a la izquierda es, cómo decirlo suavemente... - una tarea ingrata. Sólo recibirás maldiciones de los que vean tu hilo. Por cierto, es una de las razones por las que te sientes orgulloso de estar solo en tu propio hilo.
Pero para desplazar una línea periódica con un punto de inflexión hacia la izquierda en una semionda (o más bien si sólo hay un punto de inflexión entre un mínimo y un máximo local) sin un desplazamiento real se puede utilizar la derivada de esa función. Es cierto que no es un cambio real, pero en esencia. La derivada de una función es el ángulo de una tangente a la recta. Calculado simplemente: buf[i]-buf[i+1].

Aquí están, por ejemplo, la primera y la segunda derivada de una onda sinusoidal. Los puntos de inflexión de la propia función se convierten en máximos y mínimos locales de su derivada.

Sí Nikolai, estoy completamente de acuerdo contigo, y por supuesto cada derivada desplaza la gráfica del seno un cuarto de periodo hacia la izquierda.

Así que a la hora de las comparaciones eliminé el cambio de línea artificial. Esto puede verse en las segundas cifras de los últimos puestos. Todas las líneas, excepto la gris fina, se dibujan en la última barra y no se redibujan. Y algún desplazamiento del gráfico hacia la izquierda se debe a la extrapolación.

Y estas líneas sí que se pueden diferenciar, en nuestro caso eliminar la primera y/o segunda diferencia, que estaba en el prototipo. :)))

El desplazamiento hacia la izquierda se utilizó para unir todas las líneas, incluidas las de construcción, en una imagen completa, y para ver el esquema general.

 
Aleksey Panfilov:

Sí Nikolai, estoy completamente de acuerdo contigo, por supuesto cada derivada desplaza la gráfica del seno un cuarto de periodo hacia la izquierda.

Por eso, a la hora de las comparaciones, eliminé el cambio de línea artificial. Esto puede verse en las segundas cifras de los últimos puestos. Todas las líneas, excepto la gris fina, se dibujan en la última barra y no se redibujan. Y algún desplazamiento del gráfico hacia la izquierda se debe a la extrapolación.

El desplazamiento hacia la izquierda se utilizó para conectar todas las líneas, incluidas las de construcción, en el conjunto de la imagen y para demostrar el esquema general.


El gráfico superior se puede ignorar, ya que se desplaza hacia la izquierda y se redibuja la cola. Y el de abajo tiene un aspecto laxo y mundano. ¿Qué sentido tiene todo este alboroto?

 
Nikolai Semko:

El gráfico superior puede ignorarse, ya que está desplazado hacia la izquierda y la cola está sobredimensionada. Y el de abajo tiene un aspecto laxo y mundano. ¿Qué sentido tiene entonces todo este alboroto?


))))

Lo veremos "sobre la marcha".

De momento, todo va por buen camino. ))

 
Nikolai Semko:

Alexei, puedo darte un consejo gratuito y una propina.

Ya he dicho que cambiar a la izquierda es, cómo decirlo suavemente... - una tarea ingrata. Sólo recibirás maldiciones de los que vean tu hilo. Por cierto, es una de las razones por las que te sientes orgulloso de estar solo en tu propio hilo.
Pero para desplazar una línea periódica con un punto de inflexión hacia la izquierda en una semionda (o más bien si sólo hay un punto de inflexión entre un mínimo y un máximo local) sin un desplazamiento real se puede utilizar la derivada de esa función. Es cierto que no es un cambio real, pero en esencia. La derivada de una función es el ángulo de una tangente a la recta. Calculado simplemente: buf[i]-buf[i+1].

Aquí están, por ejemplo, la primera y la segunda derivada de una onda sinusoidal. Los puntos de inflexión de la propia función se convierten en máximos y mínimos locales de su derivada.


He aquí una posible aplicación de este enfoque. No hay que redibujar ni desplazar. Esta es la segunda derivada de su línea.


Archivos adjuntos:
Banzai.mq4  5 kb
Banzai.mq5  6 kb
 

A veces incluso muy correlacionados y no rezagados


 
Nikolai Semko:

Alexei, puedo darte un consejo gratuito y una sugerencia.

Ya he dicho que aplicar el cambio a la izquierda es, cómo decirlo suavemente... - una tarea ingrata. Sólo recibirás maldiciones de los que vean tu hilo. Por cierto, es una de las razones por las que te sientes orgulloso de estar solo en tu propio hilo.
Pero para desplazar una línea periódica con un punto de inflexión hacia la izquierda en una semionda (o más bien si sólo hay un punto de inflexión entre un mínimo y un máximo local) sin un desplazamiento real se puede utilizar la derivada de esa función. Es cierto que no es un cambio real, pero en esencia. La derivada de una función es el ángulo de una tangente a la recta. Calculado simplemente: buf[i]-buf[i+1].

Aquí están, por ejemplo, la primera y la segunda derivada de una onda sinusoidal. Los puntos de inflexión de la propia función se convierten en máximos y mínimos locales de su derivada.

Hoy estoy de buen humor.

Alg. en "turno a la izquierda" (qué nombre tiene :) ).

1) Consigue dos SMA, uno rápido y otro lento.

2. Desplazar un medio ciclo a la izquierda (cada uno a su aire).

3. Nos sorprende ver que :

Las formas de onda 3.0 se arremolinan unas con otras.

3.1. el rápido desplaza al lento hacia arriba justo antes del extremo (a veces mucho antes)

3.2. Cruces "por pares" (hacia arriba antes del extremo y hacia abajo después)

4. Desplazar las barras de vuelta al tiempo real, pero (a diferencia de n2) en la misma cantidad. Uno terminará en 0, el otro saldrá fuertemente hacia la derecha

5. Ahora que hemos visto el cruce del extremo pasado y el cruce anterior, vamos a ver por dónde ha pasado ya. En base a lo que podemos filtrar los falsos positivos obvios y hacer entradas bastante agradables.

 
Maxim Kuznetsov:

Hoy estoy de buen humor

Alg. en "cambio a la izquierda" (qué nombre tiene :) )

1. tomamos dos SMA, uno rápido y otro lento, según los clásicos.

2. Desplazar un medio ciclo a la izquierda (cada uno a su aire).

3. Nos sorprende ver que :

Las formas de onda 3.0 se arremolinan unas con otras.

3.1. el rápido desplaza al lento hacia arriba justo antes del extremo (a veces mucho antes)

3.2. Cruces "por pares" (hacia arriba antes del extremo y hacia abajo después)

4. Desplazar las barras de vuelta al tiempo real, pero (a diferencia de n2) en la misma cantidad. Uno terminará en 0, el otro saldrá fuertemente hacia la derecha

5. Ahora que hemos visto el cruce del extremo pasado y el cruce anterior, vamos a mirar por dónde ha cruzado ya. En base a lo que podemos eliminar los falsos positivos obvios y hacer entradas bastante agradables.


Tal vez, hay algo en él. Pero no es un algoritmo de desplazamiento hacia la izquierda, sino hacia la derecha.


12345678910111213...24
Nuevo comentario