Discussing the article: "Population optimization algorithms: Artificial Multi-Social Search Objects (MSO)"
Theoretical question (can be tested in practice).
If we add a fake (not involved in FF calculations) parameter with a range of, for example, five values to the set, will the results of the algorithm improve/deteriorate?
Forum on trading, automated trading systems and testing trading strategies.
fxsaber, 2024.02.15 11:46 AM
input int inRange = 0; void OnInit() {}

On the topic of the complexity of FF as a TC.
The standard GA finished optimisation in the green frame.
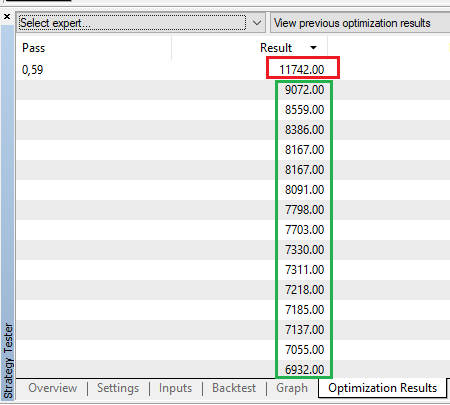
Re-starting the GA by first fumbling came to a much better result (red frame).
On the subject of the complexity of FF as a TC.
The staff GA has finished optimising in the green box.
Re-starting the GA by first fumbling came to a much better result (red frame).
For the standard GA, multiple launches are the recommended technique (I don't know whether it is good or bad - there are arguments both for and against).
Theoretical question (can be tested in practice).
If we add a fake (not involved in FF calculations) parameter with a range of, for example, five values to the set, will the results of the algorithm improve/deteriorate?
Deterioration, unambiguously. FF runs will be wasted on futile attempts to find "good" fake parameters.
The larger the percentage of possible variants of fake parameters from the total number of possible parameter variants, the stronger the impact will be - in the limit aiming for random results.
Deteriorate, unequivocally. Ff runs will be wasted on futile attempts to find "good" fake parameters.
The greater the percentage of possible variants of fake parameters from the total number of possible variants of parameters, the stronger the impact will be - in the limit aiming at random results.
I'll have to check it out.
I'd say more correctly, fake parameters make it harder to find. But all things being equal, the results will be worse. Say, if you do 1mio runs of ff, the result will be the same, but if you do 1k runs, the difference will be noticeable.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Check out the new article: Population optimization algorithms: Artificial Multi-Social Search Objects (MSO).
This is a continuation of the previous article considering the idea of social groups. The article explores the evolution of social groups using movement and memory algorithms. The results will help to understand the evolution of social systems and apply them in optimization and search for solutions.
In the previous article, we considered the evolution of social groups where they moved freely in the search space. However, here I propose that we change this concept and assume that groups move between sectors, jumping from one to another. All groups have their own centers, which are updated at each iteration of the algorithm. In addition, we introduce the concept of memory both for the group as a whole and for each individual particle in it. Using these changes, our algorithm now allows groups to move from sector to sector based on information about the best solutions.
This new modification opens up new possibilities for studying the evolution of social groups. Moving to sectors allows groups to share information and experiences within each sector, which can lead to more effective search and adaptation. The introduction of memory allows groups to retain information about previous movements and use it to make decisions about future movements.
In this article, we will conduct a series of experiments to explore how these new concepts affect the search performance of an algorithm. We will analyze the interaction between groups, their ability to cooperate and coordinate, and their ability to learn and adapt. Our findings may shed light on the evolution of social systems and help better understand how groups form, evolve and adapt to changing environments.
Author: Andrey Dik