Can the SB chart be distinguished from the price chart? - page 6

New comment
 
Vizard_:

Yes, but only on an associative level. The graphs are highly compressed. Guessing game)))
Guessing or not, Nova will tell...

I'll torture everyone for now))

 
sibirqk:


It's still pretty!

Oh, as well as I could, I know left and right))

 
Novaja:

Heredanminin writes that the difference is only in kurtosis, i.e. in islandness, from which it follows that a large number of small increments, why is this the case and the TSP is not fulfilled?

these are more increments than on sb.

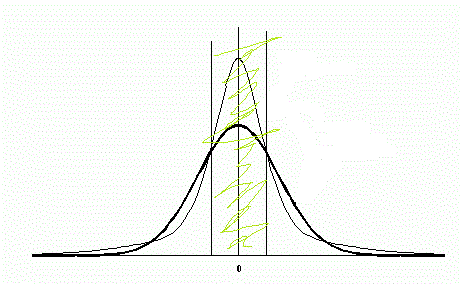
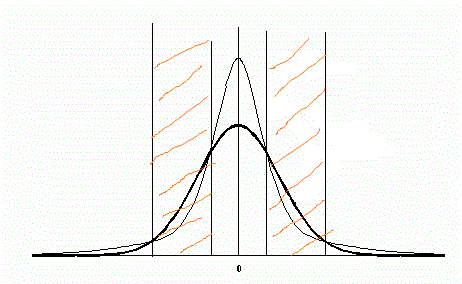
these are less.

there are more of these again.


 
Maxim Dmitrievsky:

Where is the refutation that quotes are random? And where is the proof that the whole life process of the quotes will not eventually converge to normal? And in what dimension did you measure it in the first place )

And who says that we have an infinite random process which will necessarily converge to the normal

I went through this stage a long time ago. I tried to "normalize" the market. I calculated all sorts of metrics, conducted hypothesis tests... I always drew a conclusion at the significance level of 0.9 or higher - that the price movement was not normal anywhere.

Gauss's limit theorem says that if a random variable depends on a large number of independent variables - in the limit its value is just described by the normal law.

That's the point that our random process - will never converge to normal. At most - it can only coincide with a normal distribution for a while.

 
Dmitry Fedoseev:

Let's say we flip a coin, if heads are heads up, if tails are tails down. Another 5 coins are thrown, if all are heads, we will add 5 points from the first coin - a kind of news simulation, until three eagles come out. There will be a spike in volatility. Where is the abnormality here? Why is a process like this abnormal in the real market?

Well, you're modelling just a normal random process because the flip of a coin depends on a large number of independent factors. Checking the hypothesis of uniformity of distribution - you'll probably confirm that with a high level of significance, the flip of a coin is a uniformly random process.

The actual price movement, on the other hand, is an entirely different process. And it cannot be described in terms of a uniform distribution, nor in terms of a normal distribution - again, because the price is not influenced by independent factors.

 
Georgiy Merts:

That's the thing - our random process - will never converge to a normal one. At most, it can only coincide with a normal distribution for a while.

Someone compared the movement of a price to the speed of a car, imho, a good example - at some points in time, the speed of a car obeys the laws of acceleration, then it can stop, then it can turn

Try as you might, the law of how the speed of a car changes cannot be described by a mathematical formula.


there was@Maxim Dmitrievsky's statement that a non-random process must be periodic, well, this is not a "necessary condition" for non-randomness... The same graph of an exponent is not periodic, but it won't be random either

 

one in the woods and one out of the woods...


I highly recommend reading it:

Ventzel E.S., Ovcharov L.A.

Probability Theory and its Engineering Applications

Moscow: Nauka. 1988 (Physics and Mathematics Library for Engineer). - 480 с.


Systematic account of the foundations of probability theory from the standpoint of practical applications in specialities: cybernetics, applied mathematics, computers, automated control systems, mechanism theory, radio engineering, reliability theory, transport, communications, etc. Despite the variety of fields to which the applications relate, they are all permeated by a common methodological framework.
For a wide range of engineers and scientists of different profiles, who in their practical activities face the need to set and solve problems related to random phenomena. It may also be used by university students and teachers of relevant specialities.

.

And start reading from the beginning.

 
Novaja:

Oh, as well as I could, I know left from right))

I meant Vizard_'s pictures.

 
Georgiy Merts:

So you are modeling a normal random process because the flip of a coin depends on a large number of independent factors. Testing the hypothesis of uniformity of distribution - you can probably confirm that, with a high level of significance, the flip of a coin is a uniformly random process.

The actual price movement, on the other hand, is an entirely different process. And it cannot be described either within a uniform distribution or within a normal distribution - again, because the price is influenced by far from independent factors.

How do you determine that it is an entirely different process?

 
Igor Makanu:

someone compared the movement of a price to the speed of a car, imho, good example - at some points in time, the speed of a car obeys the laws of acceleration, then it may come to a stop, then there may be a turn

Try as you might, the law of how a car's speed is governed cannot be described by a mathematical formula.


there was@Maxim Dmitrievsky's statement that a non-random process must be periodic, well, this is not a "necessary condition" for non-randomness... The same graph of an exponent is not periodic but it won't be random either

A non-random process may have a linear trend or a cyclic trend. But still there must be something that characterizes the process as non-random, otherwise it is a SB with any density of distribution

If no constant components can be distinguished, then of course the process is random, what is there to think about

A random process can pretend to be non-random, by chance. That's why in the market there is often an illusion that it is predictable, but then this period passes and all signals merge

12345678910111213...28
New comment