You are missing trading opportunities:
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register
Yes
Unfortunately, I'm not a mathematician.All you need to know is the 8th grade algebra course. You don't have to be a mathematician to do it.
The distance is marked d -- see how it is calculated.
Why is it crap? Why is it crap?
Because if you literally reproduce the code, you get nonsense that will be different on all charts.
You can't measure angles in a coordinate system that is constantly changing. Your angle will change as well.
Actually, you should tell us why you need it, maybe everyone is already using another solution for your problem.
to understand what we are talking about:
..................................................................
..................................................................
Your pictures show all the intersection points, but in fact the author has no coordinate data for the intersection points with the second line. It is not obvious from the pictures how you found it.
In fact, you should say why you need it, maybe everyone is already using a different solution for your problem.
I need to know the difference between two parallel lines ...
The red line is the distance between the lines
so far this is theory - http://www.cleverstudents.ru/line_and_plane/distance_between_parallel_lines.html but how to do it in practice ?In your pictures all the intersection points are known everywhere, but in fact the author does not have the coordinates of the points of contact with the second line. It is not obvious from the pictures how you found it.
The pictures show the whole process of solving the given problem, including the determination of the intersection points.
Oleg avtomat2018.03.31 04:30#37
The pictures show the whole process of solving the given problem, including the definition of the intersection points.
Oleg avtomat2018.03.31 04:30#37
Looking carefully at the picture (matlab apparently?)
Putting out a hypothesis, we see two functions where:
- "b" is the y-axis offset,
- "a" is the slope factor,
- "t" is the coordinate of the x-axis.
- "z(t)" is the new function that describes the perpendicular
right?
I look further and cannot figure out, the following expressions show what - where are the arrows and the inscription "solve"?
Next appears "r" (side of triangle?) - what is it and what does the formula imply by the words - degree?
Next you find d, which is sort of a well-known formula...
Looking carefully at the figure (matlab apparently?)
I put up a hypothesis, we see two functions, where:
- "b" is the y-axis offset,
- "a" is the slope factor,
- "t" is the coordinate of the x-axis.
- "z(t)" is the new function that describes the perpendicular
right?
I look further and cannot figure out, the following expressions show what - where are the arrows and the inscription "solve"?
Next appears "r" (side of triangle?) - what is it and what does the formula imply by the words - degree?
Next you already find d, sort of by the formula everyone knows...
matcad
right
"solve" = "solve" -- find the point of intersection of the line with the perpendicular, i.e. find the value of t at which y(t)=z(t)
substitute the found t and determine r=y(t) at this particular t
thus, we obtain the coordinates of the (t;r) intersection for the first line
for the second line perform the same actions
as the result we have two points, the distance between which should be determined
determine d by the formula
matcad
right
"solve" = "solve" -- finding the point of intersection of the line with the perpendicular, i.e. finding the value of t at which y(t)=z(t)
Take your time, it means solve, aha, but it's not clear how to solve. I take it through a system of equations?
Take your time, it means solving it, yeah, but it's not clear how to solve it. I take it through a system of equations?
Any way you like.
you can do it numerically, with an acceptable margin of error -- it doesn't matter.
But in this case it's very simple to solve analytically.
let me remind you that an infinite number of perpendiculars can be drawn to a given two parallel lines and any of them can be used to determine the distance
in particular is also a perpendicular to the given lines :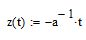
by equating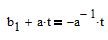
we find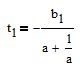
let's substitute this value in the line equation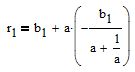
we get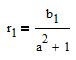
The first point (t1;r1) is found. The second is determined in the same way.
As can be seen, there is nothing complicated. One only needs to think a little.