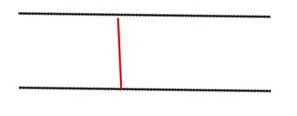
Can you tell me how to calculate the distance between two parallel lines including the scale of the graph (so that the scale is not affected)?
Here's an example:
The red line is the distance between two parallel lines - how can you calculate ?
You need to measure the distance at one point on the X axis - this is your time, I assume...
Or do you need to actually measure with an offset? Then by Pythagoras theorem - you know two sides and one angle...
Also, it depends on the distance - in pixels? Then you'd have to translate everything into the appropriate coordinate system to begin with.Can you tell me how to calculate the distance between two parallel lines including the scale of the graph (so that the scale is not affected)?
Here is an example:
The red line is the distance between two parallel lines - how can it be calculated ?
In order for the scale not to be affected, you need to use a fixed scale on the graph. Otherwise it will always be affected.
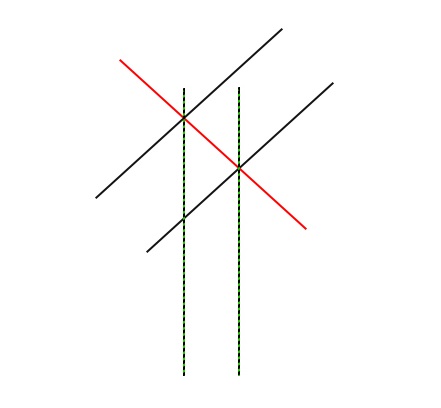
Hi!
And how can such a coordinate system be constructed, how do you imagine it ?
You have to measure the distance at one point on the X axis - that's your time, I assume...
Or do you have to actually measure with an offset ? Then by Pythagoras theorem - you know two sides and one angle...
And it also depends on what the distance is - in pixels? Then you'll have to convert everything to the appropriate coordinate system for starters.If you think logically, the red line should be perpendicular to the two (black) lines - that would measure the distance. It is NOT important to me in what values this value will be measured, the most important thing is that when you change scale, this value does not change.
I even tried to do it this way: take the value of line crossing and count the number of bars between it ... This approach is not suitable for changing the scale !
For the scale to be unaffected, it is necessary to use a fixed chart scale. Otherwise it will always be affected.
Why ? What about the proportion ?
Itum:
I do NOT care what value this value will be measured in, the most important thing for me is that when you change the scale this value will NOT change.
In that case, just measure it in pips. The lines are fixed to the price and when you change scale, the distance between them does not change, it only changes the visual representation of the lines.
I checked, the lines on the screenshots are at different scales - as you can see the distance between them does not change.
The problem with your case is that in price/second space the distance between points is not defined. Accordingly, the shortest distance cannot be found.
This is because the dimensions of the axes are different. So you must either:
- Choose a factor X between price and time, then the distance will be in units the square root of ( price x second x X ).
- count the distance along one axis;
The vertical distance is virtually unchanged with the timeframe of the chart (only because there are incomplete bars and weekend bars).
Horizontal distance does not change at all.
But when measuring distance on one axis it can be infinite, which makes no sense.
Can you tell me how to calculate the distance between two parallel lines including the scale of the graph (so that the scale is not affected)?
Here is an example:
The red line is the distance between two parallel lines - how can you calculate ?
How can you calculate the distance between two parallel lines including the scale of the graph (so that the scale is not affected)?
here's an example:
The red line is the distance between two parallel lines - how can we calculate ?
It's elementary, Watson...
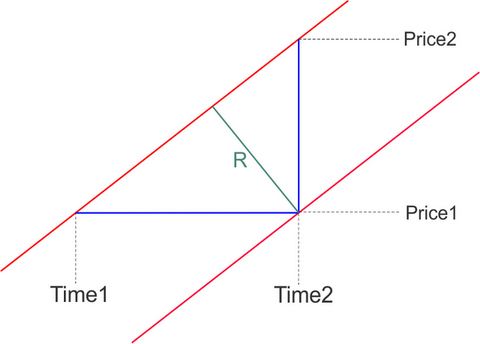
If you want to cast a two-dimensional systemPrice X Time to the plane Price X Price, you should introduce a new characteristic, which is more logically called the speed of price change V.
And it is convenient to measure it in units of units per second.
And V = tangent of the angle of your line in a system directly proportional to this one:
- 1 pixel vertically = 1 _Point
- 1 pixel horizontally = 1 second (one minute bar is 60 pixels wide on your screen)
Then the distance of two parallel lines can be calculated in two ways:
double V=(Price2-Price1)/(Time2-Time1); ulong DeltaTime = TimeLine2-TimeLine1; // double DeltaPrice = PriceLine2- PriceLine1; double R=DeltaTime*V/sqrt(1+V*V) ; // double R=V/(DeltaPrice*sqrt(1+V*V)) ; // где // точки (Price1,Time1) и (Price2,Time2) это две любые точки лежащие на одной из параллельных линий, Time измеряется в секундах // TimeLine1 и TimeLine2 - время первой и второй линии при фиксированной цене (пересечение с горизонтальной линией) // PriceLine1 и PriceLine2- цена первой и второй линии при фиксированном времени (пересечение с вертикальной линией) // DeltaPrice - расстояние между линиями в пунктах по вертикали // DeltaTime - расстояние между линиями в секундах по горизонтали // R - искомое кратчайшее расстояние между двумя параллельными линиями, скорость измерения цены которых равна V пунктов в секунду
It is clear that this perpendicular will not look like a perpendicular in a system with proportions different from those of the above system
It's elementary, Watson...
In order to bring a two-dimensionalPrice X Time system to the Price X Price plane, it is necessary to introduce a new characteristic, which is more logically called the speed of price change V.
And it is convenient to measure it in units of units per second.
And V = tangent of the angle of your line in a system directly proportional to this one:
- 1 pixel vertically = 1 _Point
- 1 pixel horizontally = 1 second (one minute bar is 60 pixels wide on your screen)
Then the distance of two parallel lines can be calculated in two ways:
It is clear that this perpendicular will not appear as a perpendicular in a system with proportions different from those of the aforementioned system
We can simplify this because there is a case where Time1=TimeLine1 and Time2=TimeLine2.
Then:
double V=(Price2-Price1)/(Time2-Time1); double R=(Price2-Price1)/sqrt(1+V*V) ;
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
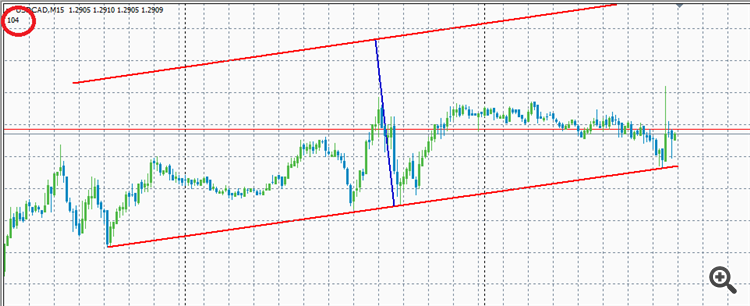
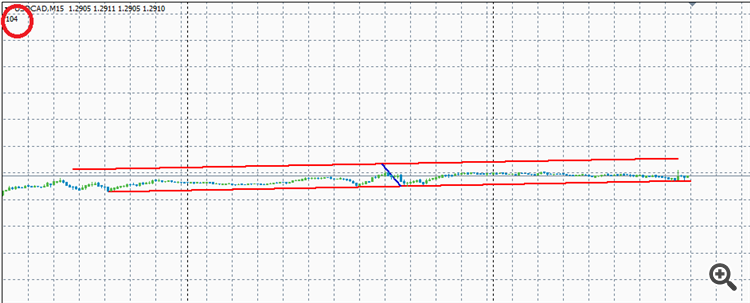
Can you tell me how to calculate the distance between two parallel lines including the scale of the graph (so that the scale is not affected)?
Here is an example:
The red line is the distance between two parallel lines - how can you calculate ?