What is difference calculus?
It is this:
Δf(xk) = f (xk+1) - f (xk)
I propose to collect indicators and experts on the difference calculus in this branch in the open source code.
I rewrote the indicator in a clearer variant as an example:
It looks like this on the chart:
The blue-red line is interpolation (finding a point within an interval) by a 4th degree polynomial with a leverage of 72.
a1_Buffer[i]=((open[i] - Znach) +5061600*a1_Buffer[i+1 ]-7489800 *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975;
The thin blue line is extrapolation (finding a point outside the interval) by the polynomial of degree 2 with shoulder 78.
a2_Buffer[i]= 3160*a1_Buffer[i] -6240 *a1_Buffer[i+1 ] + 3081*a1_Buffer[i+2 ];
The red line is the line of construction of the polynomial of degree 4. It is redrawn and based on the point of the last bar opening.
a4_Buffer[i+92]=a1_Buffer[i]; if(i<=10) { for(z=92-1;z>=0;z--){ a4_Buffer[i+0+z]= 5*a4_Buffer[i+1+z] - 10*a4_Buffer[i+2+z] + 10*a4_Buffer[i+3+z] - 5*a4_Buffer[i+4+z] + 1*a4_Buffer[i+5+z]; }}
What is difference calculus?
This kind of thing:
Δf(xk) = f (xk+1) - f (xk)
Yes.
It is directly related to Newton's binomial.
It is true for equidistant points:
1*Y1-2*Y2+1*Y3=0 is the difference equation of a straight line.
1*Y1-3*Y2+3*Y3-1*Y4=0 - the difference equation of the second degree parabola.
1*Y1-4*Y2+6*Y3-4*Y4+ 1*Y5=0 - difference equation of the parabola of the third degree.
It also overlaps with the topics:
https://www.mql5.com/ru/forum/61389/page48#comment_5633264
https://www.mql5.com/ru/forum/211220/page2#comment_5632736 .

- 2017.07.20
- www.mql5.com
Yes.
That's what everybody did... writing...
Does the future depend on the past?
That's what everyone was doing... writing...
Does the future depend on the past?
For every action, there is a trace in the present, which of course affects the future. :))))
I propose to avoid philosophy in this thread, let us focus only on mathematics, programming, testing and optimization.
Yes.
It is directly related to Newton's binomial.
It is true for equidistant points:
Y1-2*Y2+Y3=0 - difference equation of a straight line.
Y1-3*Y2+3*Y3-Y4 =0 - difference equation of the second degree parabola.
Y1-4*Y2+6*Y3-4*Y4 + Y5 =0 - difference equation of the third degree parabola.
Have you tried this formula?
Y = a0 + a1X + a2X^2 + a3X^3 + a4X^4
where:
X is the price of the previous bar;
Y - price of the current bar.
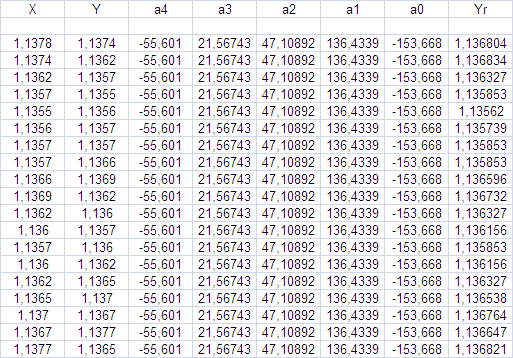
And so we get the following picture:
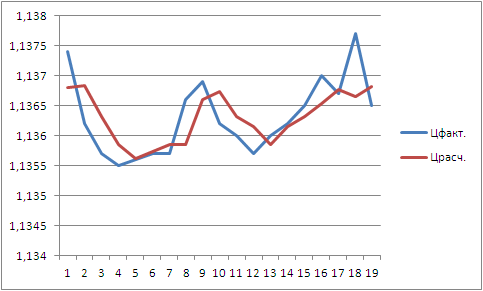
Have you tried this formula?
Y = a + bX + cX^2 + dX^3 + eX^4
Of course, in this form there are X and Y, and in the recurrence equation, only Y and all the coefficients (a + bX+ cX^2+ dX^3+ eX^4) are reduced they are replaced by the five values of Y itself.
I took a look at the code, did I get it right, this is some variant of the filter with feedback? And where did the coefficients 5061600, 4926624 and others come from?
Actually, where did the indicator come from, the Internet? ))
1. Looked at the code, I understood correctly, this is some variant of the filter with feedback?
2.And where did the coefficients 5061600, 4926624 and others come from?
3. And where did the indium come from, from the Internet? ))
1. Yes. This filter is 400 years old with only written history: Descartes, Newton, Pascal, Taylor, Lagrange.
2. Coefficients are calculated. I think in the second year we were introduced to Lagrange and Taylor methods. There seem to be a lot of variants for calculating coefficients.
3. This one in particular, I drew today. :)))))
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
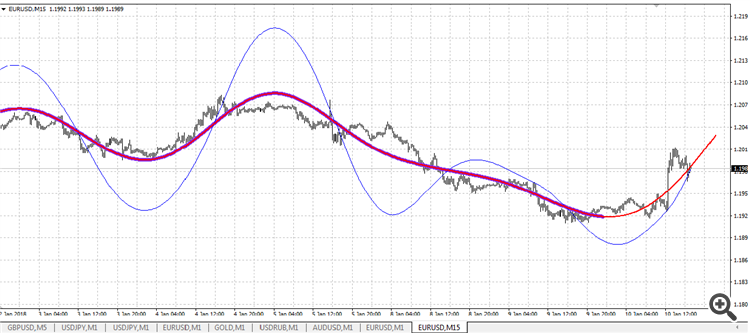
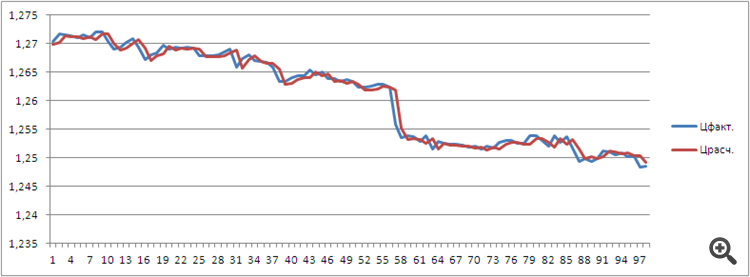
I propose to collect indicators and experts on the difference calculus in this branch in the open source code.
If there will be interest, we will eventually gather or draw something useful. :)
I have rewritten the indicator in a clearer variant as an example: