Gleitender Rumpfdurchschnitt - Seite 16

Neuer Kommentar
 
WR1:
Hallo Mladen

wenn Sie eine halbe Chance haben

Kannst du bitte dein originales HMA farbiges nrp in MTF umwandeln und es mit Interpolation versehen?

es sei denn, es ist bereits vorhanden und ich habe es verpasst

Vielen Dank

vielen Dank

WR1

Eine Version des nicht repainting multi time frame Hull moving average ist in diesem Beitrag zu finden: https: //www.mql5.com/en/forum/174961/page3 (mit Standardparametern (HMASpeed==2) ist es das gleiche wie der "normale" HMA nrp)

 

Hallo MLaden,

ich glaube, ich verstehe Sie und stimme mit Ihnen überein, wenn es um die Berechnung historischer Werte in einem höheren Zeitrahmen geht. Wir haben nur eine begrenzte Anzahl von Balken, die zusätzlichen Datenpunkten entsprechen (Balken auf der niedrigeren Zeitskala), so dass wir Interpolation, lineare quadratische usw. benötigen, um die fehlenden Balken auszufüllen oder eine Schrittfunktion zu verwenden, um die beiden Werte des höheren Zeitrahmens auf den niedrigeren Zeitrahmen zu übertragen. Sobald der Indikator jedoch gestartet ist, erhalten wir Tick für Tick Datenpunkte, die sowohl für den unteren als auch für den oberen Zeitrahmen gelten. Ich habe mich gefragt, ob es einen Indikator gibt, der die oberen Werte für die dazwischen liegenden unteren Balken berechnet und speichert. Zum Beispiel mit einem H1- und H4-Zeitrahmen. Wir können den H4-Balken berechnen und dann die fehlenden drei unteren Balkenwerte linear interpolieren, indem wir die proportionale Differenz zwischen Balken N und Balken N+1 für die Balken verwenden, die vor dem Startzeitpunkt des Indikators lagen. Ich frage mich, ob wir, anstatt für die fehlenden Balken nach dem Start des Indikators zu interpolieren, die Zwischenwerte der Stundenbalken des höheren Zeitrahmens speichern und aufbewahren können. Mit diesem Ansatz hätten wir die genauen Werte für die drei Intervallbalken. Ich bin mir bewusst, dass es eine Diskontinuität zwischen den historischen Zwischenwerten für den höheren Zeitrahmen vor dem Start des Indikators geben wird. Wenn also ein H4-Indikator von 1,0 in Takt N+1 zu 1,4 in Takt N geht, wären die interpolierten Zwischenwerte 1,1, 1,2, 1,3. In Wirklichkeit könnten die Werte jedoch 1.0, 1.3, 1.5, 1.4 sein, basierend auf den Werten zu den Zeitpunkten N, N+1, N+2, N+3.

Ich denke, was ich wirklich sagen will, ist, warum man den oberen Zeitrahmen überhaupt für einen MTF-Indikator verwendet und stattdessen die Datenpunkte des unteren Zeitrahmens verwendet, aber den oberen Indikator jeden N-ten Balken anstelle jedes Balkens vorschiebt und die tatsächlichen Werte für jedes der Intervalle verwendet.

Wenn Sie einen einfachen MTF-Indikator haben, der einen EMA verwendet, könnten Sie ihn posten, und ich werde ihn verwenden, um meine Theorie zu testen und sie zurückzuschicken.

Tzuman

 

Hallo Mladen,

Nun, ich teste und ich bin mit Ihnen ok, es ist nicht wirklich gut im Vergleich zu anderen Hull MA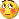

Wie ich/wir sagen, für mich muss der beste gleitende Durchschnitt schnell UND glatt sein

Also teste ich verschiedene MA (in meinem Diagramm), die ich für interessant halte

Adaptiver T3 (blau/orange)

NonlagMA (grün/rot)

JJMA (nur grün, ich habe keinen zweifarbigen JJMA)

Und ein Hull

(Tut mir leid, es ist schwierig, klar zu sein, weil ich die Linien nicht abbilden kann)

Der Zweck des Spiels war es, die MA zu vergleichen (natürlich mit unterschiedlichen Zeiträumen)

Für mich

Adaptive T3 Glatt 4/5 Schnell 4/5

Nonlag MA Glatt 3/5 Schnell 5/5

Rumpf Glatt 3/5 Schnell 3/5

JJMA Smoooth 4/5 Schnell 4/5

Also, nur eine Idee, ich denke, es könnte interessant sein, einen Rumpf angepasst durch adaptive T3 (gloups...), und ein Rumpf angepasst durch JJMA zu machen. Könnt ihr das bitte machen?

Ich habe auch 3 JMA verglichen (Spiggy, Starlight und Kositsin). Wie Sie auf dem Graphen zu sehen, ist die beste eindeutig die Kositsin in grün (JJMA), und der Wert der Starlight (und repaint)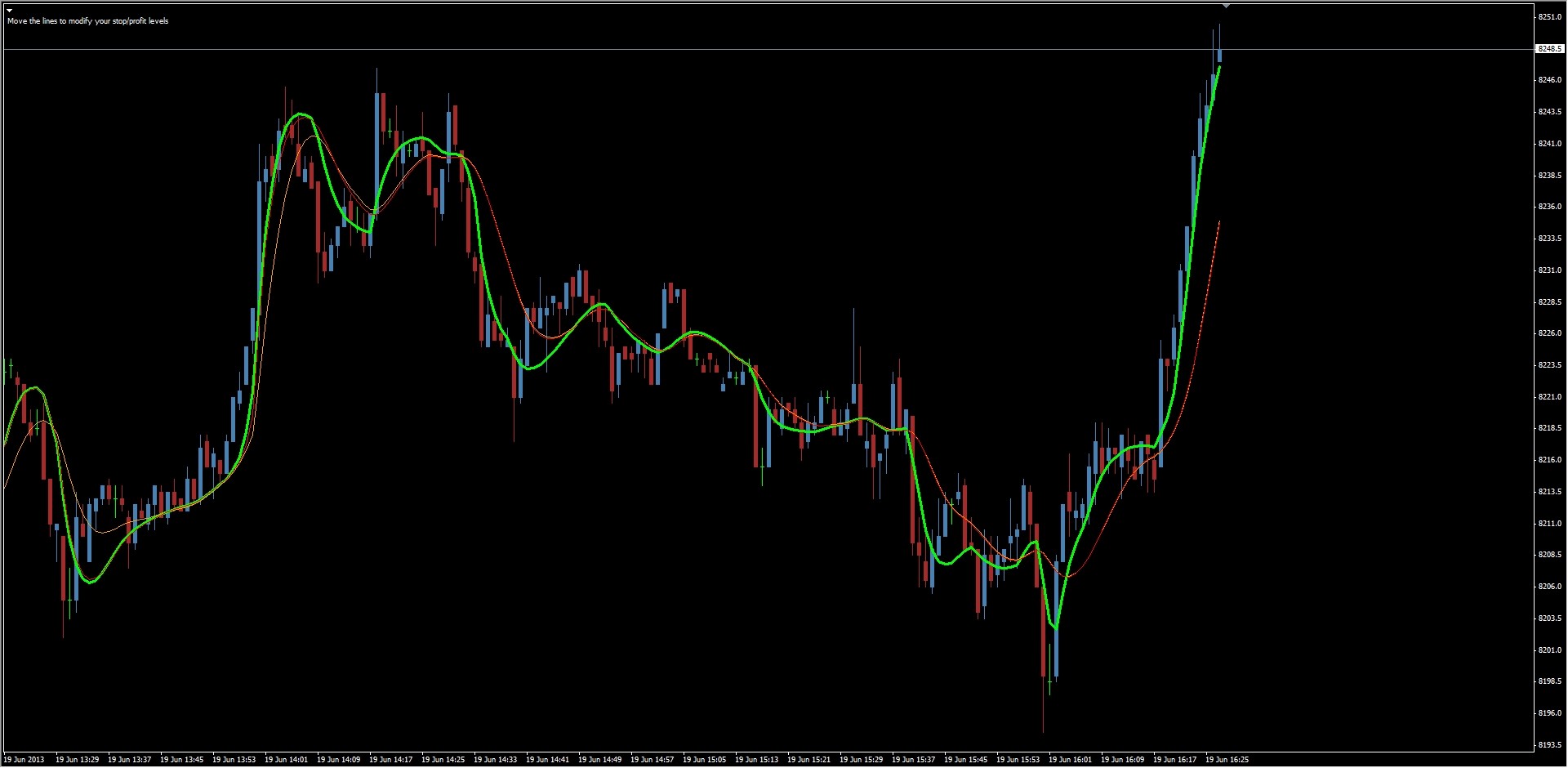 Die Adaptive T3 und die JJMA Ich benutze für den Graphen und zu erstellen, diese Hull adaptive

jjma.mq4

adaptive_t3_mladen.mq4

Tausend Dank für die Gemeinschaft Mladen

Schönes Wochenende

Zilliq

zilliq:
Vielen Dank Mladen, ich werde es versuchen, wenn ich wieder zu Hause bin.

Ich werde mit einem Hull MA und deinem NonlagMA vergleichen

Völlig in Ordnung für dich: Ich bevorzuge es, wenn es eine gewisse Glattheit gibt. Schnell und Geschmeidigkeit ist so schön...

Weißt du, ob es eine Hull-Variante T3 gibt?

Und vielleicht ist es dumm, aber Sie haben einen gleitenden Hull-Durchschnitt erstellt, der mit einem NonlagMA angepasst wurde, und Sie sind nicht zufrieden damit. Glauben Sie, dass das Ergebnis (glatter) mit einem NonlagMa angepasst mit einem Hull MA besser sein wird?

Tschüss und schönes Wochenende

Zilliq

 
mladen:
WR1 Eine Version des Hull Moving Average ohne Repainting für mehrere Zeitrahmen wird in diesem Beitrag gepostet: https: //www.mql5.com/en/forum/174961/page3 (mit Standardparametern (HMASpeed==2) ist es das gleiche wie der "normale" HMA nrp)

Danke vielmals

 
mladen:
Tzuman

Ich bin mir nicht sicher, ob ich das richtig verstanden habe.

Die Interpolationsmethode ist eigentlich ganz einfach: Es handelt sich um eine lineare Interpolation zwischen zwei Endpunkten des höheren Zeitrahmens (deshalb habe ich auch schon mehrfach darauf hingewiesen, dass interpolierte und nicht-interpolierte (die klassische "Keris-Methode") Versionen genau die gleiche Anzahl von garantiert exakten Punkten pro Bar des höheren Zeitrahmens haben: 1 pro Bar des höheren Zeitrahmens (der Rest ist eine Frage der Wahrscheinlichkeit und der Preisänderungen). Man kann die interpolierten (oder "stufenartigen") Werte weglassen (nur den aktuellen Balken des niedrigeren Zeitrahmens berechnen), aber dann erhält man einen klassischen Repainting-Indikator (da der exakte Stand zu einem bestimmten Punkt des niedrigeren Zeitrahmens in vielen Fällen nicht genau berechnet werden kann - es wäre eine wirklich komplizierte Umkehrtechnik zur Berechnung erforderlich, die Metatrader meiner Meinung nach nicht "überleben" würde)

Ich hoffe, dass ich die Frage richtig verstanden habe und dass die Antwort das ist, was Sie erwartet haben.

Hallo Mladen und Tzuman,

seit langem habe ich auch eine Frage zu diesem Thema. Wenn ich irgendeine Art von MA (z.B. Ema oder LWMA) von kleineren TF bei Price_Close mit Period_Length so eingestellt habe, dass sie mit der Länge der gleichen MA für höhere TF (z.B. EMA(H1-24 Perioden) und EMA(H4-6 Perioden)) übereinstimmen, waren sie nicht gleich. Können Sie mir das bitte erklären?

 
fareastol:
Hallo Mladen und Tzuman, seit langem habe ich auch eine Frage zu diesem Thema. Wenn ich irgendeine Art von MA (z.B. Ema oder LWMA) von kleineren TF bei Price_Close mit Period_Length so eingestellt habe, dass sie mit der Länge der gleichen MA für höhere TF (z.B. EMA(H1-24 Perioden) und EMA(H4-6 Perioden)) übereinstimmen, waren sie nicht gleich. Könnten Sie mir das bitte erklären?

fareastol

Die Multiplikation des Zeitraums, um einen höheren Zeitrahmen für die Durchschnittswerte zu erhalten, ist keine schlechte Methode (unter anderem hat Alexander Elder diese Methode in den früheren Tagen von TA verwendet), aber es ist einfach eine Annäherung. Der Grund dafür ist einfach: Die für die Berechnung der Durchschnitte verwendeten Datensätze sind unterschiedlich und man kann nicht dieselben Ergebnisse aus verschiedenen Datensätzen erhalten. Meiner Meinung nach ist es besser, das klassische MTF zu verwenden (so wie wir es verwenden), wenn auch nicht für alles andere, weil einige Indikatoren einfach nicht auf diese Weise berechnet werden können (nur ein Beispiel: versuchen Sie es mit dem RSI, und die meisten sind so)

 

Über die adaptive Funktion.

Hallo Mladen ,

Ich habe deine adaptive Volatilitätsfunktion gut studiert, warum nicht die mathematische Rundungsfunktion verwenden?

Damit (wenn ich alles verstanden habe), kann Ihre adaptive Periode mit allen Arten von gleitenden Durchschnitten oder Indikatoren arbeiten!

Mit freundlichen Grüßen.

 
sohocool:
Über die adaptive Funktion.

Hallo Mladen ,

Ich habe deine adaptive Volatilitätsfunktion gut studiert, warum nicht mit der mathematischen Rundungsfunktion?

Damit (wenn ich alles verstanden habe), kann deine adaptive Periode mit allen Arten von gleitenden Durchschnitten oder Indikatoren funktionieren!

Mit freundlichen Grüßen.

sohocool

Aus einem einfachen Grund: Wenn Sie bei einigen Durchschnitten die Berechnungsperiode ändern, erhalten Sie einen "stufenartigen" (sehr plötzlichen Wertwechsel) Durchschnitt, anstatt einen logischen, möglichst glatten Wert für diese Art von Durchschnitt zu erhalten.

Deshalb habe ich wiederholt darauf hingewiesen, dass nur Durchschnittswerte, die Bruchteile von Perioden berechnen können, zur Anpassung geeignet sind. Andere können auch angepasst werden (dafür gibt es keine Grenze), aber das Ergebnis selbst ist nicht "schön" (ich hoffe, Sie verstehen, was ich mit "schön" meine). Andererseits "erben" Durchschnittswerte wie z.B. der EMA den vorherigen Wert von sich selbst und verwenden diesen Wert bei der Berechnung, und die Berechnung kann eine gebrochene Periode verwenden, was sie ziemlich glatt und "logisch" macht, wenn die Berechnungsperiode ständig geändert wird

_____________________________

Als Experiment: Versuchen Sie, den SMA anzupassen (der aufgrund seiner Beschaffenheit nur Interger für die Berechnung der Periode erlaubt) und Sie werden sehen, wie die Ergebnisse in einigen Fällen aussehen werden

 
mladen:
sohocool

Aus einem einfachen Grund: Wenn Sie bei einigen Durchschnitten die Berechnungsperiode ändern, erhalten Sie "stufenartige" (sehr plötzliche Wertänderungen) Durchschnitte anstelle von logischen, möglichst gleichmäßigen Werten für diese Art von Durchschnitt.

Deshalb habe ich wiederholt darauf hingewiesen, dass nur Durchschnittswerte, die Bruchteile von Perioden berechnen können, zur Anpassung geeignet sind. Andere können auch angepasst werden (dafür gibt es keine Grenze), aber das Ergebnis selbst ist nicht "schön" (ich hoffe, Sie verstehen, was ich mit "schön" meine). Andererseits "erben" Durchschnittswerte wie z.B. der EMA den vorherigen Wert von sich selbst und verwenden diesen Wert bei der Berechnung, und die Berechnung kann eine gebrochene Periode verwenden, was sie ziemlich glatt und "logisch" macht, wenn die Berechnungsperiode ständig geändert wird

_____________________________

Als Experiment: Versuchen Sie, den SMA anzupassen (der aufgrund seiner Natur nur Interger für die Berechnung der Periode zulässt) und Sie werden sehen, wie die Ergebnisse in einigen Fällen aussehen werden

Hallo Mladen,

vielen Dank für deine schnelle Antwort.

Ja, ich weiß, dass deine Methode die beste ist.

Aber mit interger wird der Schritt ein kleiner Schritt sein (weniger als 1 Periode) um (14,4)=14.

und der Markt ist nicht so logisch

 
sohocool:
Hallo Mladen,

Vielen Dank für Ihre schnelle Antwort.

Ja, ich weiß, dass Ihr Weg der beste ist.

Aber mit Interger wird der Schritt ein kleiner Schritt sein (weniger als 1 Periode) um (14,4)=14.

und der Markt ist nicht so logisch

sohocool

Ich habe das Gefühl, dass Sie übersehen, dass der Berechnungszeitraum für aufeinanderfolgende Balken nicht immer ähnlich ist. Zum Beispiel: bei einem Balken wären es 14, aber bei einem anderen wären es 4. Und in diesem Fall wird es eine sehr große Veränderung haben. Wenn Sie versuchen, den SMA anzupassen, werden Sie sofort sehen, was in solchen Fällen passiert. Es ist also nicht nur der gebrochene Teil (der viel dazu beiträgt, ihn "glatt" zu halten), sondern die Tatsache, dass er eine gebrochene Periode verwenden kann, zeigt in der Regel, dass die Berechnung für die Anpassung geeignet ist (denn in den meisten Fällen, wenn die Periode gebrochen sein kann, wird der vorherige Wert des Durchschnitts in irgendeiner Form in der Berechnung verwendet, und ohne "Vererbung" ist es fast unmöglich, einen normal aussehenden Durchschnitt zu erhalten, wenn er angepasst wird)

1...91011121314151617181920212223...43
Neuer Kommentar