Warum gibt es solche Tricks mit Abschlüssen? - Seite 2

[Andrey Azatskiy]

Roman:

-0,2 ist nicht Null und führt zu einem Fehler bei der Division durch Null.

Die Funktion gibt -nan zurück, d.h. Not a Number. und der Fehler wird ausgelöst, wenn man versucht, durch -nan zu teilen. Wenn überhaupt, dann ist der Fehlertext einfach nicht angemessen.

[[Gelöscht]]

Richtige Lösung: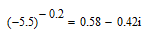 die Lösung liegt im komplexen Bereich.

Wenn es aber darum geht, unterschiedliche Lösungszweige für positive und negative Eingangsparameter zu haben, müssen wir diese Zweige erst definieren:

.

Machen Sie ein solches Feature und es wird Ihnen gut gehen. ;)

[Roman]

Andrey Azatskiy:

Die Funktion gibt -nan zurück, d. h. keine Zahl, und beim Versuch, durch -nan zu dividieren, wird ein Fehler ausgegeben. Wenn überhaupt, dann ist der Fehlertext einfach nicht angemessen.

Warum in aller Welt sollte -0,2 -nan sein?)

Eine weitere Testfunktion

Im Taschenrechner.

1/(-3 ^ 3)

-27

In mql-Funktionen

double n = 1.0/MathPow(-3.0, 3.0);
Print(n);

-0.03703703703703703

[Andrey Azatskiy]

Roman:

Warum zum Teufel ist dann -0,2 ein Nan?)

Eine weitere Testfunktion

In einem Taschenrechner

In einer mql-Funktion.

ist nicht -0,2 - nan, sondern das Ergebnis eines Anstiegs um ein Grad.
Der fraktionale Grad einer Zahl (a^m/n) ist die Wurzel aus dem Grad n von a^m.
Wenn der Subwurzelwert negativ ist, kann er entweder negativ oder positiv sein, je nach Potenz von m und der Zahl a selbst (die in meinem Problem immer negativ ist, also positiv bei positiver Potenz von m und negativ bei negativer). Wenn also der Wert der Unterwurzel negativ ist, dann ist auch die Zahl negativ. Die Wurzel einer negativen Zahl liegt im komplexen Bereich, so dass wir mit Werten des komplexen Bereichs nicht überden üblichenDouble-Typ operieren können, weshalb die Standardimplementierung von degree -nan ergibt.

[Andrey Azatskiy]

Олег avtomat:

Richtige Lösung: Die Lösung liegt im komplexen Bereich.

Wenn es aber darum geht, unterschiedliche Lösungszweige für positive und negative Eingangsparameter zu haben, dann müssen wir diese Zweige erst definieren:

.

Machen Sie ein solches Feature und es wird Ihnen gut gehen. ;)

Ich danke Ihnen für Ihre ausführliche Antwort. Aber für mich ist die komplexe Rechnung für mein Problem nicht geeignet, also werde ich mich wahrscheinlich auf die natürlichen Zahlen beschränken und damit nicht in den komplexen Bereich fallen.

[[Gelöscht]]

Andrey Azatskiy:

Ich danke Ihnen für Ihre ausführliche Antwort. Aber für mich ist die komplexe Rechnung für mein Problem nicht geeignet, also werde ich mich wohl auf die natürlichen Zahlen beschränken und damit nicht in den komplexen Bereich fallen.

Genau davon spreche ich, und ich habe Ihnen ausdrücklich ein Beispiel gezeigt. Sehen Sie es sich genau an. Dieses Beispiel ist genau auf Ihren Fall zugeschnitten.

zy

die Übersetzung in µl ist sehr einfach

[Roman]

Andrey Azatskiy:

ist nicht -0,2 - nan, sondern das Ergebnis eines Grades.
Die Potenz einer Bruchzahl (a^m/n) ist die Wurzel aus dem Grad n von a^m.
Wenn der Teilwurzelwert negativ ist, kann er je nach Potenz von m und der Zahl a selbst (die in meinem Problem immer negativ ist, also bei positiver Potenz von m positiv und bei negativer negativ ist) entweder negativ oder positiv sein. Wenn also der Wert der Unterwurzel negativ ist, dann ist auch die Zahl negativ. Die Wurzel einer negativen Zahl liegt im komplexen Bereich, so dass wir mit Werten des komplexen Bereichs nicht über den üblichen Double-Typ operieren können, weshalb die Standardimplementierung von degree -nan ergibt.

Andrey, ja, ich habe mich falsch ausgedrückt, es ist klar, dass das Ergebnis der Erhöhung auf eine Potenz -nan ergibt.
Dieses Ergebnis führt jedoch zu einer gebrochenen Potenz, wobei die ganze Zahl Null ist -0,2
Der Rechner rechnet alles richtig.

Und auch der vorherige Test zählt nicht wie im Taschenrechner.

[Andrey Azatskiy]

Олег avtomat:

Genau davon spreche ich, und ich habe Ihnen ausdrücklich ein Beispiel genannt. Schauen Sie genau hin.

Ja, ich habe es verstanden. Danke. (sogar die Formel ist aufgeschrieben)

[Aleksey Nikolayev]

Andrey Azatskiy:

Vielleicht rühren die Beine von der Tatsache her, dass man aus einer negativen Zahl keine gerade Wurzel ziehen kann? Ich bin schon ein bisschen verwirrt... Und vor allem, wie kann man sie umgehen?

Ganze Grade werden einfach durch Multiplikation (und Umkehrung bei negativen Exponenten) bestimmt und lassen sich daher leicht auf negative Basen übertragen. Gebrochene Grade werden über Logarithmus und Exponent definiert: y^x=exp(x*ln(y)) und kommen mit negativen Zahlen in die komplexe Ebene. Der Logarithmus hat unendlich viele Verzweigungen, und um sich die Suche nach der richtigen Verzweigung zu ersparen, geben sie NAN zurück.

[Igor Makanu]

Andrey Azatskiy:

Vielen Dank für Ihre Antwort, aber im Allgemeinen scheint es, wenn wir eine arithmetisch korrekte Lösung annehmen, dass nur komplexe Zahlen verwendet werden können, um eine solche Lösung zu implementieren... Bei der von Ihnen vorgeschlagenen Methode muss der Grad geteilt werden, damit der zugrunde liegende Wert immer einen positiven Grad hat und die Antwort immer positiv ist. Aber wenn man auf diese Anpassung verzichtet, kommen wir nur zu den komplexen Zahlen, denn nach dem allgemein anerkannten algebraischen Modell, das ich kenne (ich bin kein studierter Mathematiker), ist die Wurzel einer negativen Zahl eine komplexe Zahl.

Verwenden Sie die oben vorgeschlagene Formel.

Hier ist die gleiche Formel:

void OnStart()
  {
   int m = 2;
   int n = 10;
   
   double result = 1.0/pow(pow(-5.5,m),1.0/n); 		// result = 0.7110947333604484
   Print("result = ",result);
  }

und hier ein Beispiel für die Umwandlung eines Doppels in einen Bruch

https://www.mql5.com/ru/forum/290279#comment_9396706