Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Danke für den Link, ich habe mich dazu hinreißen lassen, nach ähnlichen Ideen zu suchen. Ich glaube nicht, dass man die Frage so angehen muss wie hier, aus der Perspektive der R-Funktionen. Annäherung mit konventionellen Mitteln:
Direkt aus der Gleichung eines Kreises mit dem Radius R und den Mittelpunktskoordinaten Xc, Yc, ohne Berücksichtigung des Bedeutungsverlusts von Einheiten (Zahl, Strecke, Entfernung)
R^2 = (X-Xc)^2 + (Y-Yc)^2
machen wir eine Funktion der Inkonsistenz an dem Punkt mit der Nummer i (Xi = i). Dies ist die Differenz zwischen der Entfernung vom Punkt (Xi, Yi) zum Mittelpunkt Xc, Yc und dem Radius R:
Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0,5 - R.
Die Quadrate von Di und addieren sich, um die zu minimierende Zielfunktion zu erhalten. Es gibt drei Parameter, die variiert werden können: R, Xc, Yc. Die äußersten (ersten und letzten) Punkte haben einen geringeren Einfluss als die dazwischen liegenden (nicht benachbarten) Punkte, daher halte ich es für besser, das entsprechende Di^2 mit zwei zu multiplizieren. Und für Ihre Anpassungszwecke mit Schwerpunkt auf den letzten Punkten können Sie auch mit den Gewichten mehrerer letzter Punkte spielen, indem Sie eine weitere Spalte für die Gewichte einrichten.
Wenn sie nicht gerade ist, müssen die Maßeinheiten berücksichtigt werden. Um den Einfluss von X und Y bei der Entfernungsberechnung nahezu gleich zu machen (und R wird von beiden beeinflusst), ist es notwendig, nicht die Zahl i als X zu nehmen, sondern dieselbe Zahl multipliziert mit dem Ausrichtungsmaßstab, so dass die Bereiche X und Y nahe beieinander liegen.
P.S. Es hat sich herausgestellt, dass sernam.ru sich sehr geschickt des Vorwurfs der Urheberrechtsverletzung entledigt hat, indem es die Texte der Bücher nur in Teilen und ohne Angabe der Ausgabedaten, insbesondere der Buchtitel, veröffentlicht hat. Es ist möglich, auf sernam.ru Texte zu finden, die sonst nirgendwo im Internet zu finden sind.
Ich habe herausgefunden, dass ich mit Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R minimieren muss.
Dann ist es notwendig, den gefundenen Kreis durch Spiele darzustellen.
wird die Gleichung lauten.
y=(R^2-(X-Xc)^2)^0.5+Yc
Verschwenden Sie also nicht Ihre Zeit mit dieser Richtung. Sie können jedoch einen Indikator erstellen, der auf einem Bogen und nicht auf einer geraden Linie basiert, wie der Mashka. vielleicht funktioniert er besser als der SMA.
Dies ist die Formel, die ich verwendet habe.
die allgemeine Gleichung des Bogens:
(x - L)^2+ (y + (R - H))^2 = R^2
y = sqrt(R^2 - (x - L)^2) - (R - H) , wobei die Formel für R der Abbildung zu entnehmen ist.
Aber es ist nur für die positive Ebene geeignet. Für das Experiment habe ich einen "Bogenpreiskanal" genommen, der in der positiven Ebene liegt.
vielleicht ist es nur ein hübscher Name, der gewählt wurde...
RRR5:
...
Dies ist aber nur für die positive Ebene geeignet. Für das Experiment habe ich einen "Preiskanal auf einem Bogen" genommen, der in der positiven Ebene liegt.
Was ist eine "positive Ebene"?
Was ist eine "positive Ebene"?
aber nicht in diesem Bogen.
Nun, für einen Bogen wie diesen wird es funktionieren.
aber nicht für dieses.
RRR5, du kannst schnell zeichnen. Womit, frage ich mich?
Ich lese hier über Polynome, ANC, verschiedene Näherungsmethoden, Vorhersagemöglichkeiten usw. ...
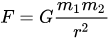
Einige glauben an Vorhersagen, andere nicht.
Aber was ich zu finden hoffte, habe ich nicht gesehen.
Um zu erklären, was ich meine, werde ich auf eine Analogie zur Schwerkraft im Universum zurückgreifen.
Hier ist ein Blick auf das animierte Gif, das ich aufgenommen habe.
Beantworten Sie sich die Frage selbst. Ist es möglich, die Flugbahn der einzelnen Objekte vorherzusagen?
Aber natürlich können Sie das.
Aber nur, wenn man Informationen über jedes Objekt im Moment kennt: seine Masse, seine aktuelle Position und Bewegungsrichtung, den Zeitpunkt seines Erscheinens und den Zeitpunkt seines Verschwindens.
Und dann geht es um Mathematik und Berechnungen, wobei im Wesentlichen nur eine Formel verwendet wird (für eine Variante der klassischen Mechanik für Geschwindigkeiten, die weit von der Lichtgeschwindigkeit entfernt sind):
Das Programm selbst ist ein Gravitationsstörer, genau hier. Sie können damit herumspielen.
Man muss auch verstehen, dass sich auch unser Planet nicht in einem geschlossenen Kreis bewegt, sondern in einer dreidimensionalen Sinuswelle (Spirale).
Dieses Video demonstriert dies deutlich:
Was ist also, wenn wir nicht über alle Objekte informiert sind?
Können wir die Flugbahn vorhersagen, wenn wir nur die Flugbahn selbst in der Vergangenheit kennen?
Hier beginnt der Spaß.
Wenn jemand sagt, dass dies nicht möglich ist, ist die Antwort falsch. Eine bejahende Antwort wäre ebenfalls falsch.
Die Lösung dieses Problems wird nur probabilistisch sein.
Das Problem muss in umgekehrter Richtung gelöst werden. Anhand der vergangenen Flugbahn müssen wir zunächst die wahrscheinlichen Flugbahnen der wichtigsten "Klumpen" von Objekten und deren Masse berechnen. Um dann probabilistische Modelle möglicher Flugbahnen vorherzusagen.
Das ist die grundlegende Aufgabe der KI - die Mustererkennung.
Soweit ich weiß, hat Maxim Dmitrievsky genau das gemeint.
Vor etwa sechs Jahren habe ich meine ersten Entwicklungen in diesem Bereich in der KB veröffentlicht:https://www.mql5.com/ru/code/10882. Ich habe dort einfach ein Polynom vom Grad 1 (lineare Regression) für die Kanalerkennung verwendet. Danach habe ich in diesem Bereich erhebliche Fortschritte gemacht. Aber ich veröffentliche nichts und werde es aus offensichtlichen Gründen auch nicht tun. Ich gebe nur Hinweise für neugierige Köpfe.
Die Suche nach linearen Kanälen besteht im Wesentlichen darin, die Zentren dieser Gravitationsmassen zu finden.
In der Regel gibt es 5-10 solcher Zentren (Kanäle) in jedem Instrument (Symbol). Für die Vorhersage des Preises sollten alle diese Faktoren gleichzeitig berücksichtigt werden. Nur in diesem Fall ist die Genauigkeit der Vorhersage nach oben oder unten viel höher als 50 %.
Aber jeder versucht, eine spezielle Reihe von Zahlen zu finden und glaubt naiv, dass sie die Zukunft vorhersagen können.
Es geht darum, dass diese "Zahlenmenge" lebendig, dynamisch ist, sie ändert sich ständig, ebenso wie sich die Lage der lokalen Massenschwerpunkte der Objektmenge analog zur materiellen Gravitation ändert. Und das Problem reduziert sich darauf, das Gesetz der Änderung dieser "Zahlenmenge" und sogar das Gesetz der Änderung des Gesetzes selbst zu finden :))
Im Idealfall sollte diese "Zahlenreihe" bei jedem Tick neu berechnet werden. Das ist genau der Grund, warum ich mehr als einmal gesagt habe, dass das, was viele als Optimierung bezeichnen, das Auffinden eines bestimmten "Zahlenpakets", ein triviales Herumbasteln an historischen Daten ist.
Ich denke, die Analogie zur Schwerkraft ist sehr treffend. Auf dem Markt wird die Schwerkraft durch Geld geschaffen. Einige werden mit 100 Dollar einsteigen, andere mit ein paar Milliarden. Hier gelten die gleichen Gesetze der Schwerkraft und sogar die gleiche Formel, die ich oben angegeben habe. Die Anziehungskraft ist umgekehrt proportional zum Quadrat des Abstands und direkt proportional zu den Massen. Daher ist eine polynomiale Regression vom Grad 2 (Parabel) das am besten geeignete Instrument. Obwohl es logischer wäre, eine Hyperbel zu verwenden, da die Wechselwirkung zweier Gravitationskörper den Gesetzen der Hyperbel folgt. Tatsache ist jedoch, dass die Parabel für Berechnungen viel geeigneter ist und dass sich Parabel und Hyperbel im wichtigsten Intervall sehr ähnlich sind.
Sie können es hier deutlich sehen. Die rote Linie ist die Parabel und die blaue Linie ist die Hyperbel.
Der Hauptunterschied zwischen der Schwerkraft des Geldes und der Schwerkraft von Himmelskörpern besteht darin, dass Geld plötzlich auftauchen und wieder verschwinden kann, was zu starken Gravitationsschwankungen führt. Aber um dieses Ereignis zu berechnen und es gibt so etwas wie einen Kanalausfall.
Die Lösung dieses Problems wird nur probabilistisch sein.
Das Problem muss in umgekehrter Richtung gelöst werden. Ausgehend von der vergangenen Flugbahn muss man zunächst die wahrscheinlichen Flugbahnen der wichtigsten "Klumpen" von Objekten und deren Masse berechnen. Um dann probabilistische Modelle möglicher Flugbahnen vorherzusagen.
Ich fürchte, die "probabilistische Lösung" wäre hier die gesamte Menge aller Flugbahnen in einem bestimmten Raum - und was ist der Wert dieser Lösung?
Das wäre so, als würde man "mit hoher Wahrscheinlichkeit" behaupten, dass der Eurodollar in diesem Jahr nicht negativ sein wird, also nicht mehr als 100. Beachten Sie, dass die Wahrscheinlichkeit für diese Behauptung bei nahezu 100 % liegt. Aber würde Ihnen eine solche "Vorhersage" viel nützen?
In der Wahrscheinlichkeitstheorie ist bewiesen, dass die Wahrscheinlichkeit eines Zustands, der von vielen unabhängigen Kräften beeinflusst wird, dem Gaußschen Gesetz zu gehorchen beginnt. Der Verlauf und der Wert der Preise gehorchen jedoch nicht dieser Verteilung, und zwar aus dem einfachen Grund, dass die Inputs und Outputs der Marktteilnehmer voneinander abhängig sind.
RRR5:
понял, что минимизировать нужно по формуле Di = ((Xi-Xc)^2 + (Yi-Yc)^2)^0.5 - R.
...
Für das Experiment habe ich einen "Preiskanal auf einem Bogen" genommen, der in der positiven Ebene liegt.
Ich verstehe immer noch nicht, warum Sie den MNC nicht mögen. Sie können jede der fraglichen Kurven aufzeichnen.
Ich arbeite gerne an kleinen TFs, aber ich mag diese Pannen nicht.
Wie kann man sie vorhersagen?