Sie verpassen Handelsmöglichkeiten:
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Registrierung
Einloggen
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Wenn Sie kein Benutzerkonto haben, registrieren Sie sich
Если параметры распределений Б и С различны, то формулы для вычисления МО и дисперсии будут сложнее, но все равно будет такое же распредление
Dies ist der Fall, wenn C und B eine stabile Verteilung haben. In diesem Fall ist die Summe der stabilen Verteilungen gleich einer stabilen Verteilung. Andernfalls, nein, die Summe oder Differenz von C und B mit unterschiedlichen Verteilungen wird eine höllische Verteilung haben.
Если оба процесса независимые, то оба они просто шум. Если ты складываешь или вычитаешь два шума, то получаешь просто третий шум. Т.е. результирующий процесс будет
y(i) = y(i-1) + e(i), где e(i) = b(i)+s(i) или e(i) = b(i)-s(i); + или - это не имеет значения.
Случайное блуждание чистой воды. Мелкие модификации, типа типа обрезания паникёров, серьёзно ничего не изменят. Только если твои процессы будут не независимые, то могут начаться чудеса.
Ich danke Ihnen für Ihre Antwort.
Darf ich eine weitere Änderung am Algorithmus vornehmen?
Wenn der Held sein "Inkrement" erhalten hat, werden seine Kräfte und Zweifel verdoppelt.
Wie würde dann dieser zufällige praxiologische Prozess aussehen?
Da Sie wissen, was Sie ähnlich modelliert haben - können Sie sich die Glocke/das Rohr ansehen?Dies ist der Fall, wenn C und B eine stabile Verteilung haben. In diesem Fall ist die Summe der stabilen Verteilungen gleich einer stabilen Verteilung. Andernfalls, nein, die Summe oder Differenz von C und B mit unterschiedlichen Verteilungen wird eine höllische Verteilung haben.
Es geht um die Modellierung von Random Walks, die in der Regel mit stationären Verteilungen - normal oder diskret - durchgeführt wird. Wir können das Problem wahrscheinlich umgehen und es als nicht-stationär modellieren. Die Summe oder Differenz nicht-stationärer Verteilungen ist in der Regel ebenfalls nicht-stationär, obwohl es Ausnahmen gibt, die z. B. der Kointegration zugrunde liegen.
Спасибо за ответ.
можно ввести еще одну поправку к алгоритму?
Если герой получил свое "приращение" - его силы и сомнения удваиваются.
Как тогда этот случайно праксиологический процесс будет смотреться?
Зная, что вы похожее моделировали - можно колокол/трубу глянуть?Ich verstehe das nicht wirklich. Wie y(i) = y(i-1) + e(i) * i, wobei e(i) = b(i)+s(i)?
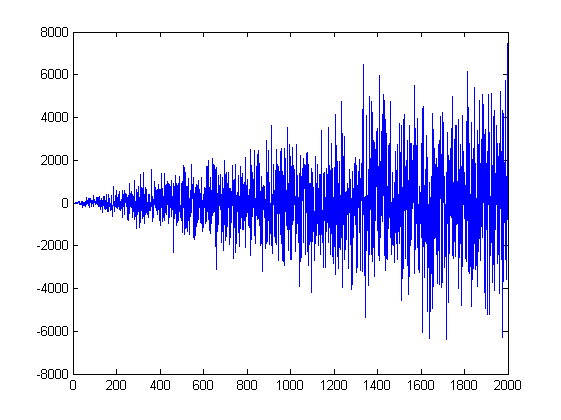
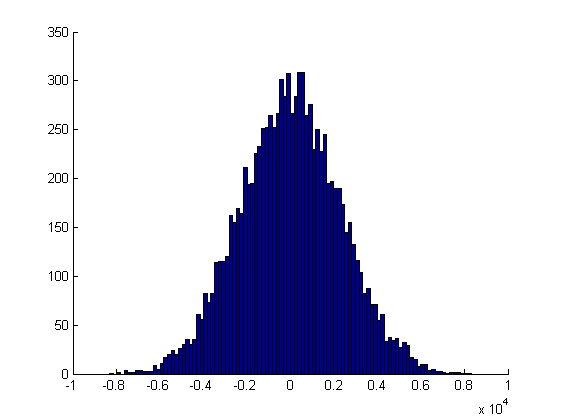
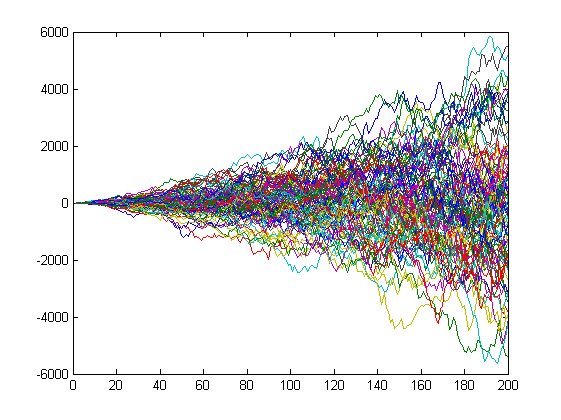
Nicht verdoppeln, aber erhöhen. Die Verdoppelung wird zu schnell wachsen. Schon eine einfache Multiplikation mit i ergibt diese Zunahme der Inkremente
Der resultierende Prozess y(i) bleibt jedoch normal, was man von einem Random Walk erwarten würde.
Auch wenn es auf den ersten Blick nicht so aussieht, ist dies nur auf den veränderten Maßstab zurückzuführen
Не очень понял. Типа y(i) = y(i-1) + e(i) * i, где e(i) = b(i)+s(i)?
Не удваивается, но возрастает. Удваивание слишком быстро вырастет. Даже простое умножение на i даёт вот такой рост приращений
Однако, результирующий процесс y(i) остаётся нормальным, чего мы и ожидаем от случайного блуждания.
Хотя оно так может и не кажется на первый взгляд, но это только из-за изменения масштаба
Zum Thema Verdoppelung gibt es folgende "praktische" Beobachtung.
Wenn der Held im vorangegangenen Schritt den gewünschten Zuwachs erhalten hat (d.h. |y(i)-y(i-1)|>= Stärke des Helden im i-ten Schritt, dann sollte seine generierte Stärke (einschließlich Minus - Zweifel) im i+1 Schritt verdoppelt werden.
Hier sollte sich der Arkussinus verstärken, aber ich bin mir nicht sicher. Die Vorzeichenabweichung ist im Weg ;)
---
Unverschämter Antrag - Erhöhung der Durchführungsdauer auf 500.
На форуме часто в пылу дискуссии утверждается, что блуждание цены абсолютно случайно.
Пускай не всегда. Но случайность и не... сложно якобы отличить.
Теоремы арксинуса и двойного логарифма периодически обсуждаются или цитируются напрямую, либо только выводы.
Мутно как то...
У меня вопрос к теоретикам и практикам.
Изучал ли кто "блуждание после соударения"?
Постановка задачи следующая - есть два условных героя "БАЙ" и "СЕЛ".
Пускай генерится некое приращение для каждого из них.
В зависимости от героя назовём их "наступательным приращением" и "оборонительной силой".
...
Hier sollte eine Fußnote eingefügt werden: Wenn es sich um einen offensiven Schritt handelt, muss er vereinbarungsgemäß Vorrang vor defensiven Schritten in der Mobilität haben,
Entweder sollte dem LFG nach der Erzeugung eine Konstante hinzugefügt werden oder es sollte ein verschobener LFG-Bereich festgelegt werden.
Dann haben wir einen offensiven und einen defensiven Teil, denn wie sollen wir sonst wissen, wer in der Defensive ist?
Zum Thema Verdoppelung gibt es folgende "praktische" Beobachtung.
Wenn der Held im vorangegangenen Schritt den gewünschten Zuwachs erhalten hat (d.h. |y(i)-y(i-1)|>= Stärke des Helden im Schritt i, dann sollte seine generierte Stärke (einschließlich Minus - Zweifel) im Schritt i+1 verdoppelt werden.
Hier sollte sich der Arkussinus verstärken, aber ich bin mir nicht sicher. Die Vorzeichen-Varianz ist im Weg ;)
Hoffen Sie, durch eine solche kaffeeblättrige Vermutung die Marktverteilung zu bestimmen (oder besser gesagt, zu passen)?
супер!
О удваивании следующее "прак...ое" наблюдение.
Если на предыдущем шаге герой получил желаемое приращение (т.е |y(i)-y(i-1)|>= сила героя на i-том шаге, то его сгенерированную силу ( в том числе с минусом - сомнения) на i+1 шаге следует удвоить.
Es gibt keinen Grund. Eine solche Manipulation wird die Verteilung der Inkremente verändern, es werden große Schwänze entstehen, selbst wenn B und C normalverteilt wären, aber sie wird die Natur des resultierenden Prozesses nicht verändern - es wird immer noch ein Random Walk sein und normalverteilt. Einem Random Walk ist die Verteilung der Inkremente egal, solange das dritte Moment Null ist, d. h. er ist symmetrisch.
речь о моделировании случайных блужданий, что делается как правило стационарными распределниями - нормальным или дискретным. Можно наверное изголиться и смоделировать нестационарным. Сумма или разность нестационарных распределений будет так же нестационарна как правило, хотя есть исключения, которые лежат в основе коинтеграциии например
Verwechseln Sie nicht warm und weich, d.h. Stationarität mit Verteilung. Sie sind in keiner Weise miteinander verwandt. Ein Random Walk hat eine Normalverteilung, ist aber nicht stationär. Eine Gleichverteilung ist stationär, aber die Summe von zwei Gleichverteilungen ist keine Gleichverteilung. Dies ist eine Eigenschaft (Beibehaltung des Typs/der Form der Verteilung bei jeder linearen Manipulation), die nur stabile Verteilungen aufweisen.
Verwechseln Sie nicht warm und weich, d.h. Stationarität mit Verteilung. Sie sind in keiner Weise miteinander verwandt. Ein Random Walk hat eine Normalverteilung, ist aber nicht stationär. Eine Gleichverteilung ist stationär, aber die Summe von zwei Gleichverteilungen ist keine Gleichverteilung. Dies ist eine Eigenschaft (Beibehaltung des Typs/der Form der Verteilung bei jeder linearen Manipulation), die nur stabile Verteilungen aufweisen.
Inwiefern ist das nicht der Fall? Die Normalverteilung ist stationär und die SB-Inkremente, die durch NR verteilt werden, sind stationär, und ich habe ursprünglich von den Inkrementen gesprochen.
Was die SB selbst betrifft (als kumulative Summe von Inkrementen): Es wird keine "dicken Schwänze" geben, wie Sie im vorherigen Beitrag beschrieben haben. Denn SB selbst ist zum Zeitpunkt t ebenfalls normalverteilt, aber mit einer Varianz, die t-mal größer ist als bei einem Inkrement (zum Zeitpunkt t vom Ursprung). Ja, die Varianz der SB-Verteilung nimmt mit zunehmender Zeit zu. Heavy Tails über 3 Sigmas zum Beispiel, aber für SB, wenn Sie die Varianz zu einem bestimmten Zeitpunkt berechnen (und Sie können es analytisch tun), wird es wie für normal sein.
Ich stimme zu, dass der SB-Prozess selbst nicht stationär ist, sondern ein inegradierter Prozess mit Einheitswurzel I(1), d. h. die erste Differenz (Inkremente) ist stationär verteilt https://www.mql5.com/go?link=http://window.edu.ru/catalog/pdf2txt/141/28141/11363?p_page=55 Aber eine nicht-stationäre Verteilung hat nicht notwendigerweise schwere Schwänze, und in diesem Fall gibt es keine.
Glauben Sie, dass HP nicht stationär ist? Oder kann man nicht für jede kontinuierliche Verteilung sagen, ob sie stationär ist oder nicht? :)