Hearst-Index - Seite 45

Neuer Kommentar
 

Version R 3.0.0 ist jetzt verfügbar.

Alles muss neu installiert werden, auch RStudio.

Übrigens, weiß jemand, wie man die obligatorischen 4 Fenster loswerden kann?

 

faa1947:  

Übrigens, weiß jemand, wie man die obligatorischen 4 Fenster loswerden kann?

Durch Ziehen der vertikalen und horizontalen Ränder können Sie nicht benötigte Fenster ausblenden.
 
WWer:
Durch Ziehen der vertikalen und horizontalen Ränder können Sie nicht benötigte Fenster ausblenden.
In der Tat, ich danke Ihnen.
 

Übrigens, falls jemand interessiert ist:

Ziehen Sie den Renko auf dem Chart bis genau zum ersten Knie des Zickzacks von und zum Pick auf.

Und am Nullknie sehen Sie die Verzögerung oder den Vorlauf des Renko-Beginns im Verhältnis zum Zigzag-Höchststand.

Das System ist wie eine Fibel aufgebaut, aber das Ergebnis ist eine Kurve im Untergeschoss, ausgehend von der Nullebene.

 

Vor nicht allzu langer Zeit brachte mich das Schicksal mit diesem Thema in Berührung, und es stellten sich sofort mehrere Fragen. Liebe Experten, können Sie mir helfen, Antworten auf diese Fragen zu finden? Treten Sie mich nicht, wenn Ihnen eine der Fragen dumm vorkommt...

Also:

1) Es gibt mehrere Möglichkeiten, den Hurst-Index zu ermitteln. Welche dieser Methoden ist Ihrer Meinung nach die beste (liefert eine genauere Schätzung des Indexes)? Wenn möglich, geben Sie einen Link zur Quelle an.

2) Sollte der Indikator bei linearen Transformationen invariant sein? (Eine ausführliche Antwort ist erwünscht).

3) Wenn die Reihen miteinander korreliert sind, was lässt sich dann über den Hurst-Index sagen?

4) Es gibt drei Serien. Für jede Reihe wird ein Hurst-Index berechnet. Was lässt sich über den Exponenten sagen, wenn die Reihen addiert werden?

Ich danke Ihnen im Voraus.

 

Sollten wir einen separaten Thread über die Verwendung der Sprache R eröffnen? Tauschen Sie Erfahrungen und Ergebnisse aus.

Natürlich nur, wenn jemand Interesse hat.

Viel Glück!

 

Ich habe mich erneut mit der Analyse dieses nicht trivialen Indikators befasst. Lange Zeit hat mich der Seitenkoeffizient verwirrt, den man durch die Berechnung des Hearst-Wertes erhält. Im Wesentlichen ist Hearst eine lineare Gleichung in doppelter logarithmischer Skala, wobei auf der Ordinatenachse (Y) die Strecke angegeben ist, die der Preis in den angepassten Skalen zurückgelegt hat, und auf der Abszissenachse (X) - ein bestimmter Zeitraum (Zeitrahmen oder Horizont). Diese lineare Gleichung ist eine Annäherung an die Punkte, die wir experimentell gemessen und aufgezeichnet haben. Die Formel für diese Gleichung ist einfach und offensichtlich:

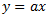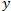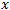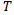Nehmen wir einmal an, dass der Koeffizient gleich Null ist, und vereinfachen wir die Formel zu . Der Wert ist hier die Strecke, die der Preis zurücklegt. Der Wert ist die Zeitspanne. Bei einer klassischen Brownschen Bewegung legt der Preis eine Strecke zurück, die der Quadratwurzel von entspricht, wobei die Zeit oder Periode ist:

Diese Gleichung ist ein Spezialfall unserer Formel unter :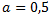

Diese Formel im doppelt logarithmischen Maßstab entspricht unserer eigentlichen linearen Funktion:

Dabei ist 0,5 der Hurst-Koeffizient.

All diese Berechnungen sind trivial, aber sie vernachlässigen den unangenehmen Koeffizienten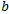 , der in der Realität fast immer eine bedeutende Zahl ist. Meine mathematischen Überlegungen über die Art dieser Abhängigkeit haben zu einem Verständnis dieses Koeffizienten geführt. Sie tritt nämlich nur dann auf, wenn wir unsere empirischen Punkte durch eine lineare Funktion approximieren. Für jeden einzelnen Punkt ist sein H immer bekannt. Er hat nicht den Koeffizienten, weil es auch für ihn keine allgemeine Näherungsfunktion gibt. Nehmen wir ein einfaches Beispiel: Versuchen wir, H visuell für die Punkte C und D R/S des EURUSD-Charts zu berechnen:

Für den Punkt C beträgt er etwa 0,45, für den Punkt D 0,51. Da beide Punkte fast genau auf der Näherungsgeraden(y = 0,5304x - 0,0757 ) liegen, können wir die genauen Werte von H für diese Punkte analytisch berechnen. Für C:

Für D:


Führt man die umgekehrte Transformation für D durch, so ist für diesen Punkt der Y-Wert 1,5155 und der X-Wert entspricht 3, dann ist sein H:

Das Ergebnis der Berechnung zeigt, dass der Punkt C antipersistent (H = 0,4547) und der Punkt D tatsächlich Brownian (H = 0,5051) ist. Die Schätzung von H für die gesamte Reihe wird bedeutungslos, da die Reihe bei einem kleinen Zeithorizont antitrendig ist, während sie bei einem größeren Zeithorizont dazu neigt, trendiger zu werden. Dies steht in vollem Einklang mit empirischen Beobachtungen über Währungen. Jeder, der lange genug mit ihnen handelt, sieht, dass die Preise auf kleinen Skalen ständig in der Ebene schwanken, und auf größeren Skalen, die ein Jahr oder länger dauern, gibt es große Trendbewegungen.

Der Koeffizient ist eine Art relativistische Korrektur in der Physik. Er bildet eine Korrelation mit H und bestimmt die Veränderung des Marktcharakters mit der Zunahme der Skala. Wenn dieser Koeffizient nahe bei Null liegt, ist der Markt in seiner Größenordnung homogen. Die Tendenz bzw. die Antipersistenz ist unabhängig von der Skala in etwa gleich groß. Wenn b signifikant ist, ist es die vorherrschende Ausgangsbedingung. H - mit zunehmender Größe wird sie immer dominanter. Hier sind die Arten der Beziehungen zwischen H und:

  • H ist größer als 0,5; b ist eine negative Zahl. Mit dieser Kombination ist der Markt auf kleinen Skalen gegen den Trend, aber wenn der Zeitrahmen größer wird, beginnen sich Trends abzuzeichnen. Das ist das Verhalten von Währungen;
  • H ist größer als 0,5; b ist eine positive Zahl. Der Markt ist homogen. Trends dominieren auf allen Zeitskalen. Wenn H signifikant und b nicht signifikant ist, sind die stärkeren Trends häufiger bei größeren Zeithorizonten zu beobachten. Je länger der Zeithorizont, desto stärker sind die Trends. Im Gegenteil, wenn H nicht beträchtlich und b groß ist, können auf kleinen Zeitskalen stärkere Trends gefunden werden, und mit zunehmender Periode treten die Trends weiterhin auf, aber ihre Stärke und Reinheit nimmt ab.
  • H ist kleiner als 0,5; b ist eine negative Zahl. Der Markt ist auf allen Ebenen antipersistent. Wenn H signifikant und b nicht signifikant ist, kommt es in größeren Zeiträumen zu einer häufigeren und saubereren Rückkehr zum Mittelwert. Auf kleineren Zeitskalen ist der Preis anfälliger für zufällige Schwankungen. Wenn hingegen b signifikant ist und H nicht, neigt der Markt bei kleinen Zeitrahmen eher zu einer Rückkehr, bei längeren Zeitrahmen nähert sich der Markt einer Brownschen Bewegung, behält aber seine Antipersistenz bei.
  • H ist kleiner als 0,5; b ist eine positive Zahl. Diese Kombination führt dazu, dass der Markt in kleinen Maßstäben im Trend liegt, bei größeren Mastschäften aber gegen den Trend geht. Offensichtlich wurde ein solches Verhalten in der Zeit beobachtet, als der Ölpreis in der Größenordnung von 100 $ pro Barrel lag.

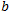Wenn b modulo ein signifikanter Teil von H ist, können Sie Ihre Analyse nicht auf H beschränken. Der Markt kann zwei gegensätzliche Eigenschaften auf verschiedenen Zeitskalen aufweisen, z. B. einen Trend und eine Gegenbewegung zur gleichen Zeit.

Wenn H und b signifikant sind und in unterschiedliche Richtungen weisen (H ist signifikant größer als 0,5 und ist negativ oder H ist signifikant kleiner als 0,5 und b ist positiv) - zeigt der Markt je nach Zeitrahmen starke Veränderungen von einem Zustand zum anderen.

 

Hat jemand die hier gezeigte Formel für den Zeitindikator umgesetzt?

http://cdn.scipeople.com/materials/2667/%D0%9F%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5%20RS%20%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0%20%D0%BD%D0%B0%20%D1%84%D0%BE%D0%BD%D0%B4%D0%BE%D0%B2%D1%8B%D1%85%20%D1%80%D1%8B%D0%BD%D0%BA%D0%B0%D1%85%202.doc

5 Länder

 
Gibt es einen Hearst-Indikator für MT4?
 
Übrigens gibt es einen Indikator, der als Invarianzindex bezeichnet wird. Sie betrachtet die Steigung der Regressionslinie und beantwortet damit die Frage, ob es einen Trend auf dem Markt gibt oder nicht. Ich habe noch keine Zeit gehabt, ihn zu benutzen, aber ich möchte, dass dieser Index nicht die Preisbewegung auf dem Markt, sondern die Bewegung der Gleichgewichtskurve berechnet. So könnte man feststellen, ob sich das Gleichgewicht ändert oder nicht. Wir bestimmen die Richtung, wenn es aufwärts geht, spiegeln wir die Signale, wenn es aufwärts geht, wiederholen wir sie. Ich habe den Eindruck, dass mit einem solchen Helfer jede Taktik an den Ohren herausgezogen werden kann .... Ich denke, jeder TS kann mit einem solchen Helfer an den Ohren herausgezogen werden, oder er kann mehr oder weniger nützlich gemacht werden... Was meinen Sie dazu?
Dateien:
ivar.mq4  4 kb
1...383940414243444546
Neuer Kommentar