Territorium der Wahrscheinlichkeit - Seite 8

[Yury Reshetov]

bowie:

Der Algorithmus zum Gewinnen eines Münzwurfspiels ist einfach: Wenn Sie Zahl erhalten, setzen Sie auf Zahl; wenn Sie Kopf erhalten, setzen Sie auf Kopf. Wenn die Anzahl der Umdrehungen unendlich ist, haben Sie gewonnen.)

Wenn die Münze krumm ist, ist die Erwartung positiv. Dies ist der Algorithmus von C. Shannon. Wenn die Münze perfekt ist und man sie wirft, bis man den Mut verliert, ist die Erwartung gleich Null, weil sie nicht von der Anzahl der Versuche abhängt.

[Ratibor Shokhirev]

Reshetov:
Если монетка кривая, тогда матожидание будет положительным. Это алгоритм К. Шеннона. Если монетка идеальная, то хоть до потери пульса подбрасывай, матожидание будет нулевым, т.к. оно не зависит от количества испытаний.

Shannon ist zweifelsohne cool, so viele Zahlen auf einmal zu bekommen. ) Mit einer Münze ist es einfacher. Kopf und Zahl bilden "Kopfstreifen" und "Schwanzstreifen", wenn genügend Würfe gemacht werden. Jedes Mal, wenn der Spieler auf die vorherige Seite setzt, hofft er, einen der Streifen mit dem Schwanz zu erwischen. Die Erwartung gleich Null wird nicht bestritten. ) Eine unendliche Anzahl von Würfen ermöglicht es dem Spieler, aufzuhören, wenn er ein ausreichendes Gleichgewicht erreicht hat.

Wenn das Spiel die Möglichkeit bietet, den Einsatz vor jedem Wurf zu erhöhen oder zu verringern, kann ein Spieler den Einsatz nach jedem Gewinn erhöhen und nach jedem Verlust verringern. Mir scheint, dass bei einem solchen Ansatz die erwartete Auszahlung etwas über Null liegen würde. Solange das Anfangskapital ausreicht.)

[Yury Reshetov]

bowie:

Shannon ist zweifelsohne cool, so viele Zahlen auf einmal zu bekommen. ) Mit einer Münze ist es einfacher. Wenn genügend Würfe gemacht werden, bilden Kopf und Zahl "Kopf-Streifen" und "Zahl-Streifen". Jedes Mal, wenn der Spieler auf die vorherige Seite setzt, hofft er, einen der Streifen mit dem Schwanz zu erwischen. Die Erwartung gleich Null wird nicht bestritten. ) Die unendliche Anzahl von Würfen erlaubt es dem Spieler, aufzuhören, wenn er genug im Plus ist.

Wenn das Spiel die Möglichkeit vorsieht, den Einsatz vor jedem Wurf zu erhöhen/verringern, kann ein Spieler den Einsatz nach jedem Gewinn erhöhen und nach jedem Verlust verringern. Mir scheint, dass bei einem solchen Ansatz die erwartete Auszahlung etwas höher als Null sein wird. Solange wir genügend Startkapital haben.

Die Wahrscheinlichkeit, dass der Spieler im Falle einer perfekten Münze früher oder später den Vorteil zu seinen Gunsten erhält, ist gleich 1, d.h. es gilt das Gesetz von Arcinus. Ob er genug Kapital hat oder nicht, ist eine andere Frage. Das Gesetz von Arcinus besagt nur, dass das Kapital bei einem konstanten Einsatz kleiner als unendlich sein muss, um einen Vorteil zu erhalten.

Ein Streifen, d.h. eine kontinuierliche Reihe von Kopf und Zahl, widerspricht keiner Theorie, bietet aber auch keine Vorteile. Wenn man Glück hat, bekommt man eine Glückssträhne. Wenn man Pech hat, hat man auch Pech. Sie hat keinen Einfluss auf die mathematische Erwartung, sondern nur auf das Glück, d. h. die Varianz und das Arkusgesetz.

[Vasiliy Sokolov]

Reshetov:

Die Wahrscheinlichkeit, dass ein Spieler im Falle einer perfekten Münze früher oder später einen Vorteil erhält, ist 1, d.h. sie gilt nach dem Arkonusgesetz. Ob er genug Kapital hat oder nicht, ist eine andere Frage. Das Arcinus-Gesetz besagt lediglich, dass man bei einem konstanten Einsatz weniger als unendlich braucht, um einen Vorteil zu erzielen.

Und Streifen, d.h. kontinuierliche Reihen von Kopf und Zahl, widersprechen keiner Theorie, aber sie bringen auch keinen Vorteil. Wer Glück hat, bekommt eine Glückssträhne. Wenn man Pech hat, hat man auch Pech. Sie hat keinen Einfluss auf die mathematische Erwartung, sondern nur auf das Glück, d. h. die Varianz und das Arkusgesetz.

Reshetov, lass den Quatsch! Was hat das Gesetz von Arcinus damit zu tun? Der Beginn einer Outperformance bedeutet nicht, dass sie ausreicht, um in den positiven Renditebereich vorzudringen, und sie wird nicht lange genug anhalten, um die Rendite im positiven Bereich zu halten.

[Vladimir Gomonov]

C-4:
Reshetov, lass den Quatsch! Was hat das Gesetz von Arcinus damit zu tun? Der Beginn einer Outperformance auf der eigenen Seite bedeutet nicht, dass sie ausreicht, um in den positiven Renditebereich zu gelangen, und auch nicht, dass sie lange genug anhält, um die Rendite im positiven Bereich zu halten.

Ihr liegt beide falsch :)

In Wirklichkeit sind alle Münzen krumm. Shannon hat also recht. Ich auch. ;)

[Ratibor Shokhirev]

Es gibt ein Skript wie dieses. Und es gibt Zweifel an MathRand(). Wer kann was sagen? )

//+------------------------------------------------------------------+
//|                                                         Coin.mq5 |
//|                                                     [e-mail] |
//|                                                     [e-mail] |
//+------------------------------------------------------------------+
#property copyright "[e-mail]"
#property link      "[e-mail]"
#property version   "1.00"
#property script_show_inputs
input int attempt=8;//количество подбрасываний
input bool z=0;//первая ставка 1 или 0 (орел/решка)
input bool as=true;//true== увеличивать лот при каждом выигрыше/ false== уменьшать

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   bool win=z;
   uint prev_count=0,tickcount=0;
   int coin=-1; 
   //int attempt=y;
   int a_rate=0;
   int b_rate=0;
   double lot=1;
   double dep=256-1;
   double div=0.0;
   bool d  = (as==true) ? div=1.009 : div=0.009;
   for(int x=0;x<attempt;x++) 
   {
    tickcount=GetTickCount();    
    while(prev_count==tickcount)
    {tickcount=GetTickCount();}
    
    MathSrand(tickcount);
    coin=MathRand()+x;
    coin=MathMod(coin,2);
    //Print(coin);
    if(coin==1 && win==1){a_rate=a_rate+1;dep=dep+lot; lot=lot*div;}
    if(coin==0 && win==0){a_rate=a_rate+1;dep=dep+lot; lot=lot*div;}
    if(coin==0 && win==1){b_rate=b_rate-1;dep=dep-lot;lot=1;}
    if(coin==1 && win==0){b_rate=b_rate-1;dep=dep-lot;lot=1;}
    if(coin==1){win=1;}
    if(coin==0){win=0;}
    prev_count=tickcount;
   }
   Print("Подбрасываний= "+attempt);
   Print("Угаданных= "+a_rate);
   Print("Неугаданных= "+b_rate);
   Print("Деп= "+dep);
  }
//+------------------------------------------------------------------+

[Boris Odintsov]

07041982:

Ich möchte hier die Methoden und Techniken erörtern, mit denen die Wahrscheinlichkeitstheorie zur Entwicklung von Handelssystemen genutzt werden kann. Ich werde meine Gedanken zu diesem Thema in Form von Thesen darlegen:

1) Die Wahrscheinlichkeit einer Trendfortsetzung in einem beliebigen Teilbereich ist zu jedem Zeitpunkt höher als die Wahrscheinlichkeit einer Trendumkehr. Daher die goldene Regel des Traders: nur mit dem Trend handeln.

2) Die Gewinnwahrscheinlichkeit bei einem zufälligen Einstieg und gleichem TP und SL tendiert mit steigendem SL und TP gegen 50%.

3) Die Gewinnwahrscheinlichkeit beim Handel mit einem dynamischen Lot ist geringer als beim Handel mit einem festen Lot. Zu diesem Schluss bin ich von selbst gekommen. Ich werde versuchen, es zu beweisen: Nehmen wir an, wir haben TS, das abwechselnd TP und SL auslöst, d.h. SL-TP-SL-TP-SL-TP, während SL = TP ist. Die Spanne wird zum besseren Verständnis nicht berücksichtigt. Beim Handel mit einem festen Lot erhalten wir zum Beispiel: -$10+$10-10$+$10-10$+$10$=0. Wenn wir mit einem dynamischen Lot handeln, werden wir -10%+10%-10%+10%-10%+10%+10% erhalten und es wird uns nicht zu einem Nullgewinn führen, sondern ein Verlust sein. Zum Beispiel, die Einlage war 100, wir erhielten: 100-10%=90; 90+10%=99; 99-10%=89.1; 89.1+10%=98.01; 98.01-10%=88.209; 88.209+10%=97.0299, was nötig war, um zu beweisen, dass der Verlust sichtbar ist.

Ich freue mich auf Ihre Kommentare und konstruktive Kritik, falls jemand mit meiner dritten These nicht einverstanden ist. Wenn jemand andere Gedanken zur Anwendung der Wahrscheinlichkeitstheorie hat, so möge er sich bitte melden.

Ich werde ein wenig verallgemeinern.

Angenommen, sl (Verlust) und tp (Gewinn) sind in Währungspunkten festgelegt.

Angenommen, wir haben eine ausreichend große Serie von N Geschäften.

N=N1+N2, wobei N1 - Anzahl der auf tp ausgeführten Geschäfte, N2 - Anzahl der auf sl ausgeführten Geschäfte.

Natürlich wird Ihr Handelssystem profitabel sein, wenn:

N1*tp - N2*sl >= Spanne * N

Rechnen Sie ruhig nach - teilen Sie den linken und rechten Teil durch N.

tp*N1/N - sl*N2/N >= Spanne

N1/N mit einer gegen unendlich tendierenden Anzahl von Abschlüssen ist nichts anderes als die Wahrscheinlichkeit eines gewinnbringenden Geschäfts, nennen wir sie p=N1/N

N2/N - dann ist die Wahrscheinlichkeit eines Verlustgeschäftes und gleich 1-p

Wir haben:

p*tp - (1-p)*sl >=Spanne

Oder anders ausgedrückt:

p>=(sl + spread)/(sl+tp)

Für diesen Zweck entwickeln wir Handelssysteme. Die Wahrscheinlichkeit, die wir erhöhen wollen. Aber man sollte sich immer daran erinnern, was es mehr sein sollte, als Gewinn zu machen.

Wenn Sie zum Beispiel den Spread ignorieren und tp und sl gleich sind, wird Ihr Handelssystem profitabel sein, wenn p>0,5 ist ... usw.

Wenn Sie Änderungen vornehmen, wie z. B. dynamische Lose, dann werden die Dinge viel komplizierter, und die Wahrscheinlichkeit eines profitablen Handels sollte höher sein als im obigen Fall.

[John]

bobsley:

Ich werde ein wenig verallgemeinern.

Wenn wir etwas mehr verallgemeinern und die reale Situation berücksichtigen, 1) MÜSSEN wir Swaps berücksichtigen 2) Wenn wir SL und TP durch Spread in Ihrer Formel ausdrücken, erhalten wir

p>= ( n_SL*Streuung + Streuung ) / (n_TP*Streuung + n_SL*Streuung) => p >= Streuung*(n_SL+1) / Streuung*(n_TP+n_SL) => p >= (n_SL+1)/(n_TP+n_SL)

Wenn wir es als Diagramm zeichnen, sehen wir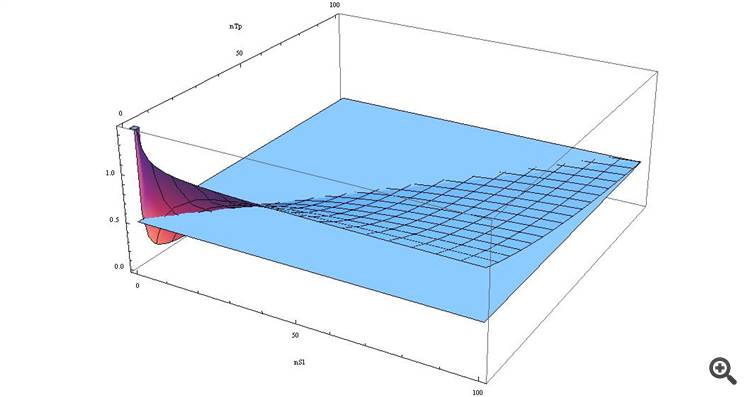

Wir sehen, dass bei SL > TP unsere Funktion größer als 0,5 ist, und je näher diese Werte sind...

Wer sich selbst davon überzeugen möchte - hier ist die Formel in Form des Wolfram-Alpha

g1 = Plot3D[(1 + nSl)/(nSl + nTp), {nSl, 0, 100}, {nTp, 0, 100}, AxesLabel -> Automatic]; 
g2 = Graphics3D[{Polygon[{{0, 0, 0.5}, {100, 0, 0.5}, {100, 100, 0.5}, {0, 100, 0.5}}], Polygon[{{0, 0, 0.9}, {100, 0, 0.9}, {100, 100, 0.9}, {0, 100, 0.9}}]}];
Show [{g1, g2}]

Eine unerwartete Schlussfolgerung für viele Menschen, nicht wahr!)

Ich erinnere mich, wie vor langer Zeit hier einige Leute riefen - was ich hier sage, dass "SL böse ist". :))

Jetzt sind die Jüngeren dazugekommen, und sie wissen jetzt mehr. :)

[Mykola Demko]

bobsley:

Lassen Sie uns ein wenig verallgemeinern.

Lassen Sie sl (Verlust) und tp (Gewinn) in Währungspunkten festlegen.

...

Wenn Sie Änderungen vornehmen, wie z. B. ein dynamisches Los, werden die Dinge erheblich komplizierter, und die Wahrscheinlichkeit eines gewinnbringenden Handels sollte größer sein als im obigen Fall.

Als rein theoretische Formel ist sie natürlich interessant, aber!!!

Wenn Sie Änderungen vornehmen, wie z. B. eine dynamische Partie, wird alles viel komplizierter...

Und wenn der Gewinn/Verlust nicht fix ist (sondern für alle Trades unterschiedlich), wird es noch komplizierter, und wenn wir dann noch den Floating Spread dazu nehmen, bekommen wir ein solches Durcheinander, dass 10 EA-Entwickler es jahrelang auf dem Tisch verteilen werden.

Deshalb habe ich versucht zu erklären, dass es schwierig ist, den Markt mit festen Mitnahme-/Verlustwerten zum Funktionieren zu bringen. Durch die Festlegung beschneidet der Systementwickler die Flügel des Systems (formal gesprochen macht er keinen Gewinn).

Und tp und sl als feste Werte werden nur benötigt, um das Konto vor Verlusten im Falle einer Unterbrechung zu schützen. Aber es gibt einfachere Lösungen als das Reparieren.

Für echte Stopps reicht es zum Beispiel aus, einen Schleppnetz-Stopp zu setzen, der in zwei Richtungen hinter dem Markt liegt und niemals auslöst, solange eine Verbindung besteht, und je nach Situation zu handeln.

Dies ist meine Meinung.

[Avals]

MetaDriver:

Ihr liegt beide falsch :)

In Wirklichkeit sind alle Münzen krumm. Deshalb hat Shannon Recht, und ich auch. ;)

In Wirklichkeit ändern die Münzen ihre Krümmung, während sie geprüft werden). Denn man kann das Experiment nicht unter genau denselben Bedingungen wiederholen wie das vorherige. Zufällige Faktoren ändern sich, und es kann durchaus sein, dass die daraus resultierende Krümmung für eine lange Zeit unausgewogen ist. Das heißt, es geht um die Änderungsrate der Zufallsfaktoren im Verhältnis zum Experiment. Wie ihre interne Zeit mit der Zeit zwischen den Experimenten korreliert.

Angenommen, es wird ein Zufallsprozess auf der Grundlage einer einzelnen Sinuskurve erzeugt. Wenn zum Zeitpunkt des Experiments der Wert des Sinus>0, dann Kopf, weniger als das - Schwanz. Und dann hängt alles von der Periodizität unserer Experimente, der Genauigkeit der Zeitberechnung und der Periode der Sinuswelle ab. Wenn die Intervalle zwischen den Experimenten nicht fest sind und viel länger sind als die Periode der Sinuswelle, dann erscheinen die Werte zufällig. Wenn die Zeit zwischen den Experimenten mit einer Genauigkeit eingestellt werden kann, die der Periode der Sinuswelle entspricht, wird die Reihe nicht zufällig sein - bis hin zu deterministisch (je nach Genauigkeit der Zeitmessung).

Im Allgemeinen müssen Zufallsprozesse nicht periodisch sein, aber ihre Zyklizität und die Summe aller Zufallsfaktoren müssen vorhanden sein. Zum Beispiel kann es keine kontinuierlich ansteigende Funktion anstelle einer Sinuskurve geben - dann hätte die resultierende Reihe einen Aufwärtstrend. Zufällige Prozesse, die sich auf die Reihe auswirken, sind in Wirklichkeit alle nicht zufällig)))) nur gibt es keine Informationen, um ihre Phase zum Zeitpunkt des Experiments genau zu messen, oder die Messgenauigkeit ist unzureichend.

Wenn die Summe der "zufälligen" Faktoren im Verhältnis zu 0 ausgeglichen ist (wie im Beispiel mit der Sinuswelle) - d. h. wenn sie über 0 und unter 0 liegt, dann hat die Reihe unter dem Einfluss dieser Faktoren mo = 0. Liegt die Summe längere Zeit über 0, gibt es eine Schieflage zugunsten von Kopf oder zugunsten von Zahl. D.h. die Summe der Zufallsfaktoren ist in gewissem Sinne ausgeglichen und zyklisch. Wir kennen nur nicht seinen genauen Wert zum Zeitpunkt des Experiments.

Die Realität wird jedoch durch die Tatsache erschwert, dass sich die Zufallsfaktoren und ihre Summe ändern können. Zuerst war es eine Sinuswelle)), dann wurde es zu einer geraden Linie mit einem Winkel, wenn diese Analogien zutreffen. Deshalb besteht die Aufgabe des Handels darin, solche Momente zu erwischen, wenn die Serie eine Trendkomponente hat, die nach oben oder unten geht. Dies erfordert die Korrespondenz mit den zugrunde liegenden Prozessen. Renditeprozesse wie eine Sinuskurve bilden Renditemuster (wie Flat-Trading), schiefe Prozesse bilden Drift (Trend). Im Allgemeinen besteht die Aufgabe darin, einen Prozess in einem seiner Stadien zu erkennen und das nächste Stadium zu kennen. Die Schwierigkeit besteht darin, dass es viele dieser Miniprozesse gibt, dass sie unterschiedlich groß sind und dass sich ihr Einfluss mit der Zeit einfach ändert (Amplitude, wenn man die Analogie zu einer Sinuswelle heranzieht).