AIS Adaptive Nonlinear Smoothing
- 指标
- Aleksej Poljakov
- 版本: 1.0
- 激活: 5
很多时候,在金融系列的研究中应用他们的平滑。使用平滑,您可以删除高频成分 - 据信它们是由随机因素引起的,因此无关紧要。平滑总是包括一些平均数据的方法,其中时间序列中的随机变化相互吸收。大多数情况下,为此目的,使用简单或加权移动平均方法,以及指数平滑。
这些方法中的每一种都有其优点和缺点。因此,简单的移动平均值简单直观,但其应用需要时间序列的周期和趋势分量的相对稳定性。另外,信号延迟是移动平均值的特征。指数平滑方法没有滞后效应。但即使在这里也存在缺陷 - 只有在将系列与随机异常值对齐时,指数平滑才有效。
简单和指数平均值之间的合理折衷是使用加权移动平均线。但是,存在选择特定重量值的问题。让我们一起尝试解决这个问题。
因此,首先要定义我们希望从平滑过程中实现的目标:
•首先,我们需要从价格序列中删除随机变化和噪音;
•其次,我们希望识别异常排放和异常价格行为,这些行为也可用于贸易;
•最后,平均程序应确定市场中存在的可持续趋势。
当然,我们希望平滑程序适应当前的市场情况。
为了获得理想的结果,我们将根据此价格水平与研究期间的最高和最低价格之间的差异来计算权重。通过这种方法,我们得到一个过滤器,根据感兴趣的时期的价格分布实现平滑过程。
这种平滑算法的主要优点是其在各种排放方面的稳定性:价格偏差可能非常大,但过滤器仍将遵循最重要的趋势。另外,对于不同的初始数据,我们可以在其本质效果上有所不同。因此,如果价格或多或少均匀分布,那么我们将得到一个移动中值滤波器。如果价格累积在一个值附近并且最大值和最小值之间存在足够大的差异,则我们得到模态平滑。如果所有价格都在非常窄的区间内,那么我们得到一个简单的移动平均线。
该方法的主要缺点是在不考虑价格随时间变化的情况下进行平滑。实际上,我们可以在分析期内任意改变价格的顺序 - 这不会影响计算结果。因此,我们可以说该算法将价格变化视为随机过程。
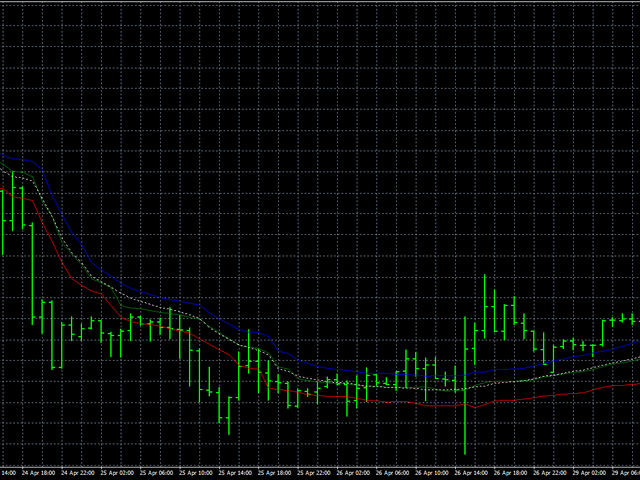
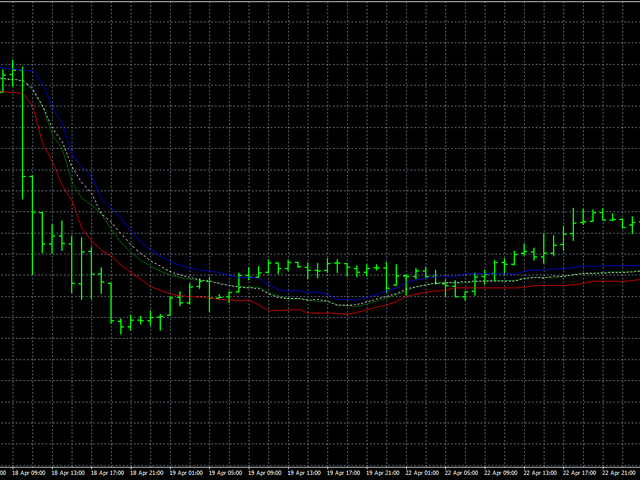
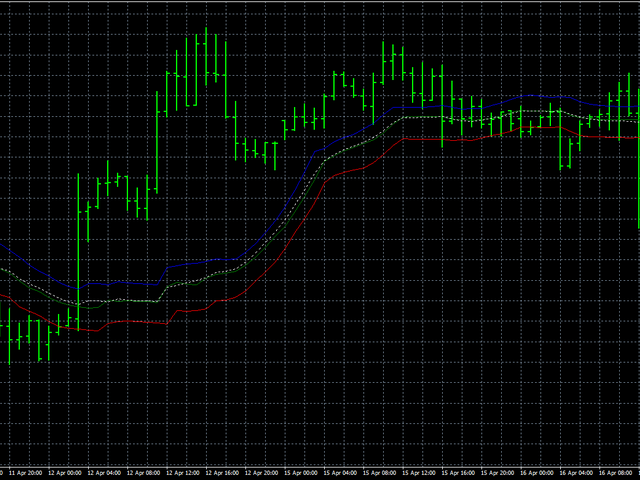
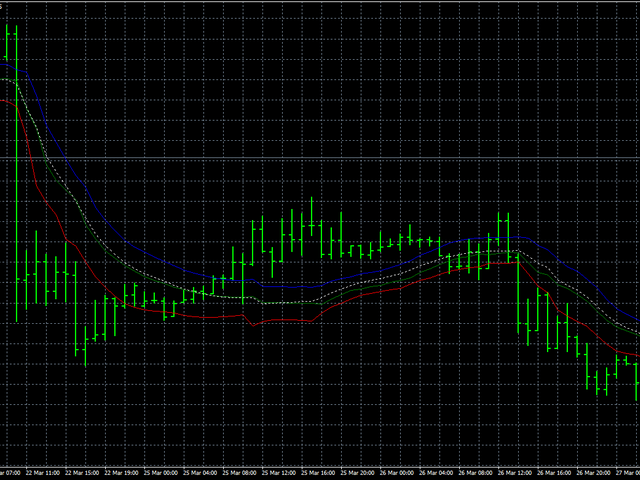
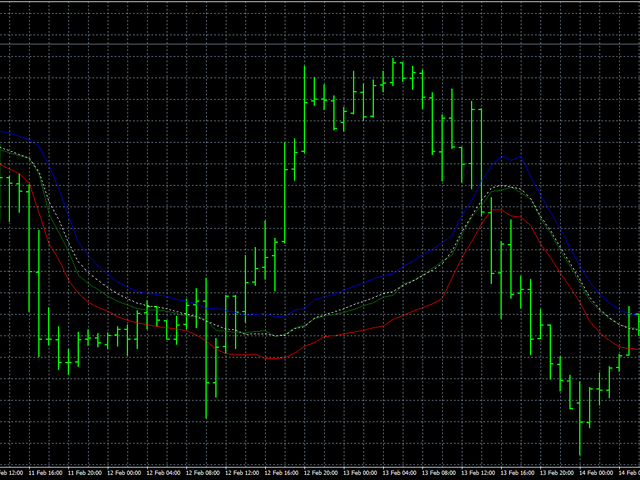
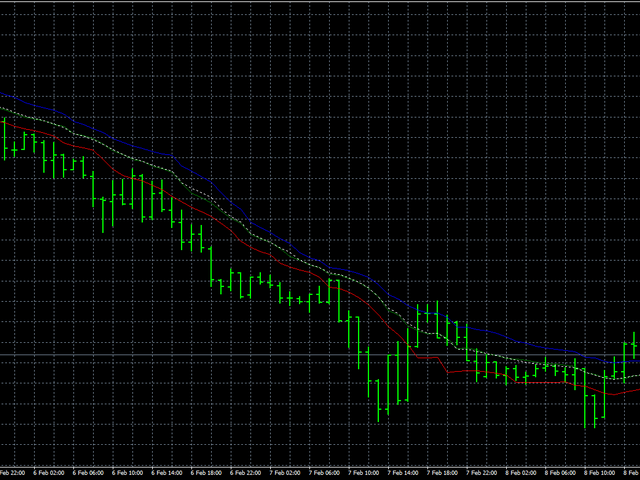
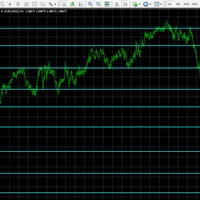
尽管有这个缺点,让我们看看这个算法如何在真实数据上运行。在这种情况下,我们按如下方式进行:首先,我们将开放,高和低的价格相互分开,然后将所有价格放在一起。同时平滑所有价格将使我们能够判断价格行为的稳定程度。蓝线将显示高价格的平滑,红线 - 低线,绿线将显示开盘价格的平滑。白色虚线表示同时平滑所有价格。
- LH是一个参数,用于设置用于分析的柱数。它的允许值在0到255之间,而实际的条数是一个。