Рантье - страница 16
Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Интересно посмотреть, как эти параметры влияют на результат:
Например, для наших исходных условий, при различных положениях вентиля, получаем такие интересные картинки
.
.
.
Ну это для общей картины...
Нас же интересует здесь именно последняя зависимость
( фазовый портрет "a - da" -- последний график -- её частный случай )
Ничего путного не получилось. Вычисления сюда не буду выкладывать. Ничего красивого в них нет.
Пытался использовать следующее наблюдение: 1+q-k = 1+epsilon, причем epsilon - малая величина. Далее раскладывал производную по k в ряд Тейлора, удерживая вначале члены до третьего порядка малости. Затем, после упрощений, получилось кубическое уравнение. В нем я отбросил член третьего порядка малости по epsilon и попытался решить полученное квадратное. Не вышло: дискриминант положителен только при небольших t.
Боюсь, что совершил ошибку, отбросив кубический член: он хоть и является членом третьего порядка малости по epsilon, но малым не является. Он у меня был таким: epsilon*epsilon*(epsilon-q)(t-1)(t-2)(t-3). Видно, что при больших t он может быть совсем немалым (даже если epsilon~0.01 - вполне реалистичное допущение). А кубическое решать не хочется.
Посмотрим, что получится у Олега.
P.S. При допущении epsilon*t = О(1) (или q*t =О(1) ) можно аппроксимировать степенную функцию экспонентой. Попробуем...
Есть еще один подход - без рядов Тейлора, а просто методом касательных (кажись, Ньютона). И до довольно точного аналитического решения можно тоже добраться.
Дело в том, что изначально в условиях фигурирует не непрерывное время, а решётчатая функция -- т.е. прежде необходимо произвести соответствующее преобразование. Только тогда введение малой epsilon будет правомерным. Таковы свойства решётчатых функций.
Кстати говоря, именно переводом в область непрерывного времени я занимался на первом шаге решения задачи, используя преобразование Лапласа в цепочке дискреты--частоты--время. Вернее сказать: в том числе, и этим...
Итак, объектом нашего дальнейшего анализа является функция
.
А кубическое решать не хочется.
Алексей, мне ни разу не приходилось видеть аналитическое выражение для корней кубического уравнения (кроме частных упрощённых случаев). У тебя часом нет такого? Что бы прямо как для квадратного уравнения: x1=b/2+SQRT()... и т.д. Выложи если знаешь. Я в Инете ничего не нашёл. Помню из школы, что есть даже представление корней через гармоническиме функции!
Есть еще один подход - без рядов Тейлора, а просто методом касательных (кажись, Ньютона). И до довольно точного аналитического решения можно тоже добраться.
Что, действительно, таким способом можно получить приближённое решение в аналитическом виде? Никогда не слыхал. Очень интересно, хочится увидеть реализацию метода на примере.
В студию!
Да, ты говоришь о полученном решении для больших t. Это тоже представляет практический интерес, как случай "неубиваемого" депозита. Для каких t тебе удалось получить приближение? Может возможен предельный переход для t->inf... Тогда, мы получим на руки аналитическое выражение для оптимального процента выводимых средст - k, как функцию всего одного параметра q - величины начисляемых процентов. Это был бы великолепный результат.
avtomat:
Дело в том, что изначально в условиях фигурирует не непрерывное время, а решётчатая функция -- т.е. прежде необходимо произвести соответствующее преобразование. Только тогда введение малой epsilon будет правомерным. Таковы свойства решётчатых функций.
Кстати говоря, именно переводом в область непрерывного времени я занимался на первом шаге решения задачи, используя преобразование Лапласа в цепочке дискреты--частоты--время. Вернее сказать: в том числе, и этим...
Олег, почему ты считаешь, что полученное выше аналитическое выражение для суммы выводимых средст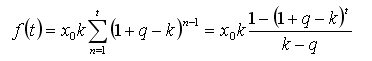
не является предельным для непрерымного времени? Ведь, мы не где специально не оговаривали ограничение на минимальный интервал (шаг) исходного временного ряда (итерационная форма записи в первом посту топика). Если так, то достаточно того, что при предельном переходе при dt->0 мы имеем определённую df(t) и нет противоречия...
Олег, почему ты считаешь, что полученное выше аналитическое выражение для суммы выводимых средст не является предельным для непрерымного времени? Ведь, мы не где специально не оговаривали ограничение на минимальный интервал (шаг) исходного временного ряда (итерационная форма записи в первом посту топика). Если так, то достаточно того, что при предельном переходе при dt->0 мы имеем определённую df(t) и нет противоречия...
не так... Попытайся ввести сюда малую epsilon...
Да, мы нигде специально не оговаривали, но сама формулировка задачи неявно подразумевает использование решётчатой функции.
Это значит, что совпадение будет в узлах решётки. Мало того, для решётчатых функций нет промежуточных точек -- только узлы решётки. Поэтому попытки построения промежуточных значений ведут к ошибочным результатам (кстати говоря, эти вопросы -- из области квантования сигналов). Для построения промежуточных значений можно увеличить частоту дискретизации, т.е. ввести опять же решётчатую функцию с бОльшим количеством узлов, что принципиально не изменит сути явления. Это, в частности, означает, что вместо первой, второй и т.д. производных используются первые, вторые и т.д. разности. Вместо интегралов -- суммы. ... и т.д. -- это целая область исследований.
Но есть пути перехода из одной области в другую и обратно.
Нас в данном конкретном случае решения поставленной задачи -- такой подход не устраивает. Поэтому первым делом мы должны перейти от дискретного времени к непрерывному.
Дело в том, что изначально в условиях фигурирует не непрерывное время, а решётчатая функция -- т.е. прежде необходимо произвести соответствующее преобразование.
мне ни разу не приходилось видеть аналитическое выражение для корней кубического уравнения (кроме частных упрощённых случаев). У тебя часом нет такого? Что бы прямо как для квадратного уравнения: x1=b/2+SQRT()... и т.д. Выложи если знаешь. Я в Инете ничего не нашёл.
Формула Кардано
Помню из школы, что есть даже представление корней через гармоническиме функции!
Тригонометрическая формула Виета
... или не производить, а пользоваться имеющимся аппаратом дискретного вариант преобразования Лапласа, т.е. Z-преобразования. Не кажется, что получится проще?
да это как раз не проблема. В самом начале есть картинка трёхмерная "%роста - %съёма - доходность" -- всё уже посчитано, и именно в дискретной области.
Сейчас спортивная задача состоит в том, чтобы представить это всё в виде аналитическом ;)
Формула Кардано
Тригонометрическая формула Виета