Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Не знаю, у меня написано, что это за формула и все переменные определены. Еще уточню - это размер прибыли снимаемой каждый месяц (не общая прибыль на m месяцев).
Осталось вывести формулу суммы ряда, вы писали, что лекго это делаете - сделайте. Затем взять производную, приравнять к нулю...
В моих обозначениях ваша формула для выведенных в текущем месяце средств выглядит так:
Соответственно, раздолбить звероподобную производную от этой функции так же трудно, как и выше приведённую.
Я думаю, что можно попробывать предварительно пролагорифмировать f и затем уже искать её максимум... Может так будет легче.
avtomat:
А потом уже, на втором шаге, откроем вентиль, разделяющий поток на две части. При этом изменится входной поток.
Пока не видишь решение?
Не, не врубаюсь пока как именно ты задумал. Рассказывай.
есть такие, что и теорему Пифагора в их интерпретации не разберешь.
ОФФТОП:
В школе давали самое лаконичное доказательство теоремы Пифагора.
Заметьте, основная простейшая (нестандартная) мысль - п.2. Никакие знания свойств подобных треугольников не используются, Также для понимания существования функции f никаких знаний тригонометрии тоже не нужно. Т.е. такое доказательство можно давать в начальной школе после того, как хорошо (а не как обычно) объяснят детям, что такое площадь.
ОФФТОП:
В школе давали самое лаконичное доказательство теоремы Пифагора.
в каком классе?
формула S = c^2 * f(alpha) для 7-классника не очевидна. Это принятие на веру, что типа так и есть.
Соответственно, раздолбить звероподобную производную от этой функции так же трудно, как и выше приведённую.
Весь процесс уперся в производную?
Вот эта функция - x0*k*(1-(1+q-k)^2)/(k-q)?
Если это так, то это как бы не проблема, я их легко решал, только вспомнить надо немного. Переменная q?
в каком классе?
формула S = c^2 * f(alpha) для 7-классника не очевидна. Это принятие на веру, что типа так и есть.
Почти любой ребенок, которого хорошо познакомили с понятием площади фигуры так, что он это почувствовал, не испытывает особых трудностей с пониманием вышеприведенного доказательства.
Если ребенок по-настоящему понимает, что такое площадь, то он понимает меру ее измерения и понимает также, что площадь любой фигуры можно выразить через ее характеристики (в данном случае гипотенуза и угол), определяющие однозначно фигуру.
Никакого знания свойств подобных треугольников и тригонометрии не надо.
Был недавно в гостях, и видел две каменные пирамидки (по типу египетских). Взял их в руки и приложил основаниями (они немного разные по размеру):
И придумал ещё одно доказательство теоремы Пифагора (понятно из построения).
Integer:
Весь процесс уперся в производную?
Вот эта функция - x0*k*(1-(1+q-k)^2)/(k-q)?
Если это так, то это как бы не проблема, я их легко решал, только вспомнить надо немного. Переменная q?
Нет, проблема в производной по k от: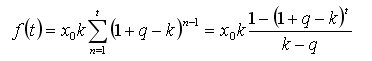
Ее нужно приравнять к нулю и решить относительно k.
Я по умному не осилю, нарисую по простому:
Допустим, на депо 10 000 в начале периода. Каждый период на депо начисляется 5% и их-же реинвестируем на депо. Разрешается каждый период снять только 3%.
Если снимать каждый период все свои 3%, то всего наснимаем более 4к$ (и чхать на депо), в противном граничном случает получим только 0.5к$ (зато на депо много).
Почти любой ребенок, которого хорошо познакомили с понятием площади фигуры так, что он это почувствовал, не испытывает особых трудностей с пониманием вышеприведенного доказательства.
Если ребенок по-настоящему понимает, что такое площадь, то он понимает меру ее измерения и понимает также, что площадь любой фигуры можно выразить через ее характеристики (в данном случае гипотенуза и угол), определяющие однозначно фигуру.
Но это не строгое доказательство.
Я по умному не осилю, нарисую по простому:
Вот для того и нужно общее аналитическое решение, чтобы не рисовать подобные таблицы, а подставить в простенькую формулку два входных значения и получить ответ.
в том и дело, что все вышесказанное это "оно чувствуется, что типа так будет". Что "это как то можно выразить через что-то".
Но это не строгое доказательство.
Какое не строгое доказательство?! Это же очевидно: