[Архив!] Чистая математика, физика, химия и т.п.: задачки для тренировки мозгов, никак не связанные с торговлей - страница 309
Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
YUBA, фраза в "случайном порядке" тут не совсем подходит.
Ну короче, ответ (337) - единица.
Т.е. Вы можете назвать такую расстановку чисел, при которой единица, стоящая на сотом месте, никуда не сдвинется ни в первый, ни во второй раз?
P.S. Задача чем-то напоминает самую первую в этой ветке (о Пете): кажется, будто условий не хватает, и подходит чуть ли не любое число.
Теперь понял. Буду думать :) Только завтра, сейчас уже не соображаю.
Ну ты даешь. Я надеялся на интригу...
Доказывай.
Да не умею я доказывать.. И не люблю... Ну не моё это...Моё дело искать ответы. // И находить!... :)
// Блин. А ведь раньше любил. Хлебом не корми, бывало, дай только чего-нить подоказывать.
.....
Лан попробую. Сначала укажу на тот факт, что нахождение "100" на 100-м месте ещё недостаточное условие неподвижности, а только необходимое.
Кроме этого все числа меньшие сотни должны быть исходно на местах меньших 100 (в любом порядке). Остальные, соответственно, на оставшихся - тоже в любом порядке.
Попробую доказать от противного. // вот такой уж я противный.
Если хотя бы одно число на местах 1..99 >= 100, то при первом проходе оно будет захвачено сортировочным процессом и станет перемещаться слева направо, до тех пор пока не встретится с ещё большим числом. Если это произойдёт - далее оно останется "на месте встречи", а вместо него поползёт вправо новое максимальное число. Пересекая "границу" (100) максимальное число неизбежно "подвинет" стоящее там число, если оно окажется меньше его. На этом анализ первого прохода можно прекратить и перейти ко второму. Если хотя бы одно число в диапазоне "числомест" 101..1982 меньше или равно 100, оно будет захвачено процессом и начнёт двигаться влево.... и т.д. (см. описание первого прохода в зеркале). Таким образом есть только один способ оставить неподвижным число на 100 месте: поставить туда число 100 и обеспечить чёткую предварительную группировку всех чисел меньше 100 - слева от 100, и всех больших - соответственно справа.
Вот и всё что я могу сказать по этому поводу. Понятия не имею, насколько это тянет на доказательство, но очевидность я вроде обеспечил. // По крайней мере для себя )))
По мнению моей тещи: это число 1981, а не 100 :)
Все равно не хватает. Где контакты, между которыми измеряется ток? Сетка может быть полубесконечной с началом в начале координат и первым контактом. Тогда достаточно перекусить два.
А если один из контактов - где-нить в центре сети, то достаточно четырех - вокруг него.
Согласен. Счас переделаю. :)
Можно и в такой формулировке.
Dim a, b, с, d, i, z As Long
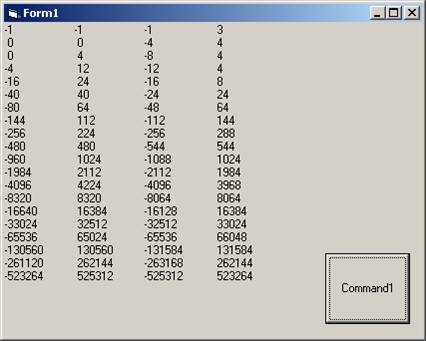
Private Sub Command1_Click()
a = 1
b = 2
c = 3
d = 4
For i = 1 To 20
z = a
a = a - b
b = b - c
c = c - d
d = d - z
Print a, b, c, d
Next i
End Sub
Dim a, b, с, d, i, z As Long
Private Sub Command1_Click()
.......... ...
Next i
End Sub
..........
// Кстати, удивителен факт, что степени двойки представлены в последовательности в огромном количестве. Тоже неизбежность?