Всем привет..
У меня вопрос по преобразованию Фурье..
После преобразования Фурье и фильтрации высоких частот с обратным преобразованием,
требуется продолжить расчет полученной функции вне диапазона преобразования (если можно на примере)..
Далее ничего уже не надо рассчитывать, т.к. Фурье преобразование эффективно применяется только к периодическим функциям.
Допустим на полученом диапазоне у нас периодический сигнал,
следствие - начало массива - это есть продолжение периодической последовательности .. Так?
Допустим на полученом диапазоне у нас периодический сигнал,
следствие - начало массива - это есть продолжение периодической последовательности .. Так?
Какого массива?
Фурье преобразование выполняется на аппроксимируемом периоде от 0 до 2 * PI.
2*PI - это 0 градусов для следующего периода, аппроксимация для которого уже выполнена на предыдущем периоде.
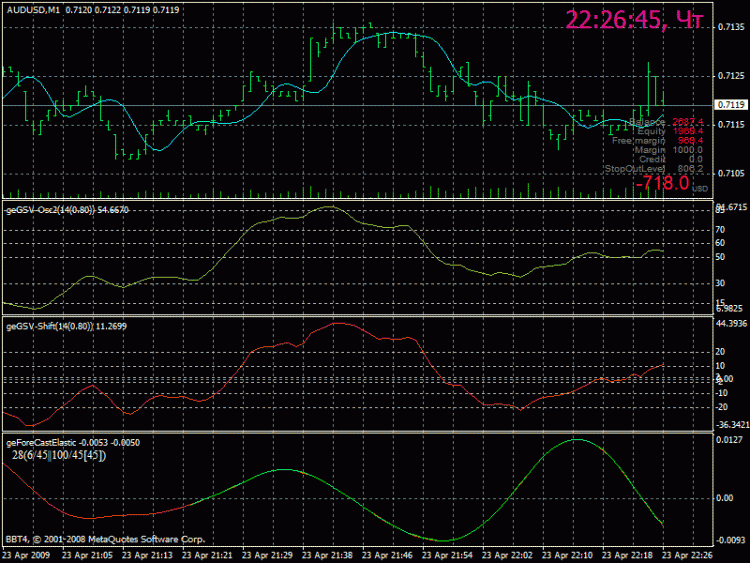
Тогда посмотрим на рисунок..
на нижнем индикаторе находится кривая (красный цвет) зеленная это линия полученная в процессе преобразования с параметрами
размер окна преобразования 2^6=64 точки, кол-во используемых частот 45.
т.е. мы получаем подобие результирующей кривой.. которую наложили на исходную..
как видно из рисунка подставить начало в конец - это не реальный результат -
Вот вопрос и состоит в том как продолжить движение кривой показаное зеленной линией..
....
Вот вопрос и состоит в том как продолжить движение кривой показаное зеленной линией..
В этом весь фокус от Фурье и ему подобных преобразований!
Вы сначала приведите нестационарность рынка в квазистационарный вид, хоты бы...
Потом можете превратить всё в стационарные синусоиды и продолжать их куда хотите. Но... Наверно, у Вас ничего не получиться...
Может тогда поставить вопрос в другом плане ..
Каким способом можно аппроксимировать показанную функцию на рисунке что бы можно было бы продолжить движение кривой на небольшом участке?
Может тогда поставить вопрос в другом плане ..
Каким способом можно аппроксимировать показанную функцию на рисунке что бы можно было бы продолжить движение кривой на небольшом участке?
На небольшом участке можно воспользовать любым аппроксимационным методом, используя его для экстраполяции.
Я Лагранжем пользуюсь.
Тогда посмотрим на рисунок..
на нижнем индикаторе находится кривая (красный цвет) зеленная это линия полученная в процессе преобразования с параметрами
размер окна преобразования 2^6=64 точки, кол-во используемых частот 45.
т.е. мы получаем подобие результирующей кривой.. которую наложили на исходную..
как видно из рисунка подставить начало в конец - это не реальный результат -
Вот вопрос и состоит в том как продолжить движение кривой показаное зеленной линией..
1. С какого перепуга Вы решили, что взятые для аппроксимации 64 точки являются периодической функцией?
2. Количество гармоник не может превышать половину взятых отсчётов, т.е. если аппроксимация по 64 делениям периода, то максимальная гармоника будет 31-й
3. Нереальный результат потому что Вы взяли непериодическую функцию для аппроксимации, а соответственно и продолжение периода не будет совпадать. Вам же уже сообщали, что ПФ эффективно только на периодических функциях, все остальное - танцы с бубном.
Нужно брать два одинаковых периода: 0 - 2*PI, 2*PI - 4*PI. По обоим гнать ПФ и сравнивать, есть ли совпадения по амплитудам и фазам гармоник. Если нет, то значит функция непериодическая и период отсчета нужно либо увеличивать, либо уменьшать (уменьшать или увеличивать - это уже смотреть по сдвигам фаз для отдельных гармоник)
, все остальное - танцы с бубном.
Нужно брать два одинаковых периода: 0 - 2*PI, 2*PI - 4*PI. По обоим гнать ПФ и сравнивать, есть ли совпадения по амплитудам и фазам гармоник. Если нет, то значит функция непериодическая и период отсчета нужно либо увеличивать, либо уменьшать (уменьшать или увеличивать - это уже смотреть по сдвигам фаз для отдельных гармоник)
В принципе, это тоже "танцы с бубном", только с более "навороченым". Результатом будет "более красивое" разрисовывание истории - не более.
Периодическая - это такая функция, для которой существует такое Т, что для любого х верно следующее равенство f(x) = f(x+T). Тогда Т и есть период функции f(x).
Говоря проще - у трейдера нет гарантии, что при выборе Т по предложенному алгоритму (как общее кратное двух последовательных периодов) третий период такого же размера выборки будет сответствовать выбранному значению (а третий - это как раз тот период, на который делается экстраполяция). Нет гарантии при любом алгоритме выбора Т.
И, кстати, - если функция периодическая - на кой этот фурье сдался ? Никто не задумывался ? Нашли период и подставляйте значения - всего делов то ;). Эт, конечно, если нашли период, а не сплясали с бубном....
Успехов.
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Всем привет..
У меня вопрос по преобразованию Фурье..
После преобразования Фурье и фильтрации высоких частот с обратным преобразованием,
требуется продолжить расчет полученной функции вне диапазона преобразования (если можно на примере)..