Вы упускаете торговые возможности:
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Регистрация
Вход
Вы принимаете политику сайта и условия использования
Если у вас нет учетной записи, зарегистрируйтесь
Сильная сглаженность тоже не даёт хороший результат - увеличение профита. Увеличение сглаженности по-любому приводит к увеличению задержки. Но даже если допустить мысль, что мы имеем нулевую задержку, то увеличение сглаженности приведёт к пропуску более мелких движений, что соответственно приведёт к уменьшению колличества сделок, соответственно уменьшению профита и соответственно увеличению просадок.....
Даже на графике хорошо видно, что часть достаточно больших движений, которые теоретически можно было бы взять - не взята, соответственно прибыль уменьшилась.....
Сильная сглаженность тоже не даёт хороший результат - увеличение профита. Увеличение сглаженности по-любому приводит к увеличению задержки. Но даже если допустить мысль, что мы имеем нулевую задержку, то увеличение сглаженности приведёт к пропуску более мелких движений, что соответственно приведёт к уменьшению колличества сделок, соответственно уменьшению профита и соответственно увеличению просадок.....
Подстраивайтесь адаптивно под оптимальный вариант.
Вами описанный случай - это беда всех зависимых от времени индикаторов. Отказывайтесь от времени в классическом понимании и используйте иные методы.
Я уже давно отказался от таких ТС и использую другие методы....Просто написал пост, как мнение, о том, к чему может привести увеличение сглаженности )))))
Я уже давно отказался от таких ТС и использую другие методы....Просто написал пост, как мнение, о том, к чему может привести увеличение сглаженности )))))
А можно вам письмецо отписать?
Плюс к этому всему нужно всё-таки добавить ошибки(убытки) от увеличения задержки(не нужно быть альтруистами) и вопрос профита может ваще повиснуть в воздухе.....))))
Насчет авторства идеи готов поспорить. Скорее всего этой идее столько же лет сколько и самой МАшке. :))
А вообще-то тема для меня интересная – сам ею занимаюсь. Естественно не всё так красиво как у тебя на рисунке. Там явно не хватает очень многих стрелочек.
Теперь по порядку:
Я пока считаю что без агрессивного ММ такая система профита не даст.
Чтот ж, товарищ! - Значит верным путём идём.
На рис. очень схематично, это иллюстрация метода открытия/закрытия позиций.
1. Аргумент спорный (равенство нулю второй производной), поэтому требует аргументации с твоей стороны. Что касается экстремума (равенство нулю первой производной), то тут вроде аргументация не нужна.
2. Требование близости МА к котиру и одновременное требование её гладкости не конфликтуют (и не могут, а дополняют друг друга). Яркий тому пример обычная экспоненциальная средняя ЕМА. Её рекурсивная форма получается именно из минимизации функционаала, требующего близости и гладкости одновременно.
3. Это можно рассматривать как развитие метода. Для начала, необходимо получить решение для очевидных требований к виду функционала.
Swetten писал(а) >>
Прошу прощения, что такое "ФЗ"?
ФЗ - фазовая задержка. Термин из ЦОС.
TheXpert 19.01.2009 14:45
За основу берется целевая функция по ссылке на наметки?
Сильная сглаженность тоже не даёт хороший результат - увеличение профита. Увеличение сглаженности по-любому приводит к увеличению задержки. Но даже если допустить мысль, что мы имеем нулевую задержку, то увеличение сглаженности приведёт к пропуску более мелких движений, что соответственно приведёт к уменьшению колличества сделок, соответственно уменьшению профита и соответственно увеличению просадок.....
Может попробовать последовательно?
Сделать исходный вариант, проанализировать.
Типа нравится там-то, не нравится тут-то, поэтому то-то убираем нафек, а тут наворачиваем.
Просто я смотрю тут разброд и шатания, а изначальная мысль была классная.
Может попробовать последовательно?
Сделать исходный вариант, проанализировать.
Типа нравится там-то, не нравится тут-то, поэтому то-то убираем нафек, а тут наворачиваем.
Просто я смотрю тут разброд и шатания, а изначальная мысль была классная.
Никакого разброда!
Если пожеланий более нет, то освежим в памяти основные требования к идеальной МА:
1. Близость к исходному ВР. Это требование равносильно малости расстояния между котиром Х (зелёная линия на рис.) и cглаженной кривой Y (синяя). Можно записать, что в среднем, по большой выборке должно свыполнятся: (X[i]-Y[i])^2-->min
2. Гладкость МА. Это требование равносильно малости расстояния между соседними отсчётами гладкой кривой: (Y[i]-Y[i-1])^2-->min
3. Кривая Эквити, которая будет состаять из нарубленных из исходного ВР кусков с учётом направления (знака) открываемых позиций (между вертикальными линиями на рис), должна быть растущей. Знак открытия позиции, равен знаку производной МА. В наших обозначениях sign(Y[i]-Y[i-1]). Кривая эквити в этом случае будет складываться из кусков котира, которые будут сшиваться встык, согласно знаку закрываемой позиции. Реализовать это можно так. Построим для котира ряд первой разности (РПР) d[i]=X[i]-X[i-1], тогда исходный ВР леко востанавливатся из РПР по алгоритму: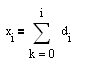 , тогда быстрый рост кривой эквити (
, тогда быстрый рост кривой эквити (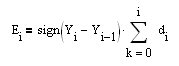 ), равносилен требованию максимализации первой производной от неё: dE[i]/dt=E[i]-E[i-1]= sign(Y[i]-Y[i-1])*(Х[i]-Х[i-1]) или с небольшим, но допустимым, в нашем случае натягом {(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->max Очевидно, что максимизация некоторого выражения, равноссильна минимизации его же с обратным знаком: -{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min.
), равносилен требованию максимализации первой производной от неё: dE[i]/dt=E[i]-E[i-1]= sign(Y[i]-Y[i-1])*(Х[i]-Х[i-1]) или с небольшим, но допустимым, в нашем случае натягом {(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->max Очевидно, что максимизация некоторого выражения, равноссильна минимизации его же с обратным знаком: -{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min.
Всё. Получаем так необходимый нам функционал для минимизации:
S=w1*(X-Y)^2+w2*(Y[i]-Y[i-1])^2-w3*{(Y[i]-Y[i-1])*(Х[i]-Х[i-1])}^2-->min
Его-то минимум относительно Y[i], где i - текущий отсчёт, нам и нужно найти.
Никакого разброда!
Если пожеланий более нет, то освежим в памяти основные требования к идеальной МА:
ИМХО, не хватает вида функции Y. Или я что-то пропустил?
Отлично, нашли такое решение для какого-то временного промежутка. Дальше что?
Как что? Зарабатываем -- профитноть вложена в целевую функцию.