Preciso interpolar uma função com ajustes arbitrários, por isso escolhi estrias.
Entendo corretamente que obterei interpolantes diferentes pelo número de pontos de nodo, o que mais posso variar?
E a segunda pergunta, o que é melhor escolher para a interpolação a partir da lista, se eu preciso apenas construir muitas interpolações diferentes da série original (a variação é importante)
O que é melhor escolher é uma questão muito delicada. Uma abordagem, chamada minimização empírica de risco, é desenvolvida no livro de Wapnick Algoritmos e Programas de Recuperação de Dependência. 1972, ao que parece.
O que é a melhor escolha é uma questão muito delicada. Uma abordagem, chamada minimização empírica de risco, é desenvolvida no livro de Wapnick "Algoritmos e programas para a reconstrução da dependência". Parece que estamos em 1972.
Maximização da probabilidade/imização do risco empírico, como eu o entendo, é apenas um nome geral para os algoritmos correspondentes. Não preciso do algoritmo em si, só preciso modificar as curvas, de preferência rápida e variavelmente, com possibilidade de encontrar valores interpolantes em novos pontos (o pacote spline permite este último).
Maximização da probabilidade/imização do risco empírico, como eu o entendo, é apenas um nome geral para os algoritmos correspondentes. Não preciso do algoritmo em si, só preciso modificar curvas, de preferência rápidas e variáveis, com possibilidade de encontrar valores interpolantes em novos pontos (o pacote spline permite este último)
Tanto o método de máxima probabilidade quanto o de minimização (lembro-me, não empírico, mas médio) do risco são nomes não de algoritmos, mas de formas de estabelecimento de metas no estabelecimento de problemas. Se a meta é atingível, ela dá origem a algum algoritmo que é necessariamente consistente com a meta, é uma implementação de sua realização em casos particulares. Se você não precisa de objetivos ou algoritmos para alcançá-los, nenhum conselho pode ser dado para a tarefa de escolher funções de interpolação. Você pode escolher como seu coração lhe diz...
Preciso interpolar uma função com ajustes arbitrários, por isso escolhi estrias.
Entendo corretamente que obterei interpolantes diferentes pelo número de pontos de nodo, o que mais posso variar?
E a segunda pergunta, o que devo selecionar para a interpolação da lista, se eu precisar apenas construir muitas interpolações diferentes da série inicial (a variabilidade é importante)?
O mais valioso para um comerciante não é a interpolação e não a aproximação, mas a extrapolação.
As estrias não são adequadas para extrapolação.
Tenho grande experiência e compreensão em polinomial aproximação-extrapolação. Menos experiência é Fourier.
Extrapolação por métodos polinomiais e Fourier são completamente diferentes na natureza. A extrapolação de Fourier só pode ser aplicada ao mercado plano devido à sua natureza periódica (esta linha é uma soma de sinusóides de diferentes freqüências, fases e amplitudes), e tende sempre a voltar atrás,enquanto a extrapolação polinomial, ao contrário, é boa para a tendência, pois sempre tenta "voar para cima" ou para baixo devido à sua natureza de grau.
Portanto, faz sentido combinar estes dois métodos para obter bons resultados de extrapolação.
A aproximação polinomial é de particular interesse para os programadores porque este tipo de aproximação é muito bem otimizada e pode ser calculada muito rapidamente. Consegui sair dos ciclos para o cálculo dos coeficientes.
Também é importante lembrar que todos os tipos de aproximação criam linhas redesenháveis a cada novo ponto. Somente o traçador da linha aproximada não é redesenhado.
Uma aproximação polinomial tem apenas uma solução, em oposição a uma aproximação de Fourier. Isto permite a criação de slides únicos não redesenháveis:
Vejo que adivinhar ao acaso também não é ruim. Portanto, ninguém resolveu problemas semelhantes. Vou visualizá-lo, vou ver.
Ninguém o resolveu - errado. Todos os métodos de interpolação têm sua justificativa teórica e geralmente um objetivo claro. Por exemplo, o defeito cúbico dois estrias minimizam a energia potencial de flexão elástica de uma régua passando através dos pregos martelados na tábua nos nós da estria. Desta forma, uma curva suave (defeito inferior a 3) foi obtida a partir de uma tabela de pontos em um desenho com o contorno de um navio ou um perfil de asa. As mesmas estrias retratam a deflexão de uma viga multi-suporte em matemática resiliente. Muitas vezes o objetivo é minimizar a soma das deflexões de coordenadas nos nós de interpolação. Para comparar os resultados da interpolação com diferentes objetivos é necessário um objetivo generalizado, um critério que é computável para qualquer método de interpolação. Ela se baseia no número de coeficientes a serem determinados. Grosso modo, se uma aproximação polinomial com um aumento do grau polinomial de 3 para 7 reduz a soma dos quadrados de desvio em 20%, então o grau 3 é mais razoável do que 7. O analógico na engenharia de rádio, se não estou confuso, é a freqüência de corte do filtro.
A coisa mais valiosa para um comerciante não é a interpolação ou aproximação, mas a extrapolação.
As estrias não são adequadas para extrapolação.
Tenho grande experiência e compreensão em polinomial aproximação-extrapolação. Menos experiência - Fourier.
Extrapolação por métodos polinomiais e Fourier são completamente diferentes na natureza. A extrapolação de Fourier só pode ser aplicada ao mercado plano devido à sua natureza periódica (esta linha é uma soma de sinusóides de diferentes freqüências, fases e amplitudes), e tende sempre a voltar atrás,enquanto a extrapolação polinomial, ao contrário, é boa para a tendência, pois sempre tenta "voar para cima" ou para baixo devido à sua natureza de grau.
Portanto, faz sentido combinar estes dois métodos para obter bons resultados de extrapolação.
A aproximação polinomial é de particular interesse para os programadores porque este tipo de aproximação é muito bem otimizada e pode ser calculada muito rapidamente. Consegui sair dos ciclos para o cálculo dos coeficientes.
Também é importante lembrar que todos os tipos de aproximação criam linhas redesenháveis a cada novo ponto. Somente o traçador da linha aproximada não é redesenhado.
Uma aproximação polinomial tem apenas uma solução, em oposição a uma aproximação de Fourier. Isto permite a criação de slides únicos não redesenháveis:
Tudo bem. Não tenho nada a extrapolar, é a interpolação que é necessária. Quero dizer que não faz sentido fazer uma previsão com base em tal extrapolação. É necessário que esta linha seja tão forte quanto possível, de um lado ao outro, como sua linha azul. E quero poder obter uma solução sobre os novos pontos, sim (sem recalcular com base na fórmula existente).
Por isso, basta perguntar o que é melhor usar - polinômios ou estrias ou alguma subespécie. E talvez o 10º grau também fosse divertido.
Ninguém o resolveu - está errado. Todos os métodos de interpolação têm sua justificativa teórica e geralmente um objetivo claro. Por exemplo, o defeito cúbico dois estrias minimizam a energia potencial de flexão elástica de uma régua passando através de pregos martelados na tábua em nós da estria. Desta forma, uma curva suave (defeito inferior a 3) foi obtida a partir de uma tabela de pontos em um desenho com o contorno de um navio ou um perfil de asa. As mesmas estrias retratam a deflexão de uma viga multi-suporte em matemática resiliente. Para comparar os resultados da interpolação com diferentes objetivos é necessário um objetivo generalizado, um critério que é computável para qualquer método de interpolação. Ela se baseia no número de coeficientes a serem determinados. Grosso modo, se uma aproximação polinomial com um aumento do grau polinomial de 3 para 7 reduz a soma dos quadrados de desvio em 20%, então o grau 3 é mais razoável do que 7. O analógico na engenharia de rádio, se não estou confuso, é a freqüência de corte do filtro.
É só que se eu começar a tentar explicar tudo o que vou fazer com ele, vão ser novamente algumas páginas :) Você precisa de variabilidade, diferentes graus de polinômios, número de pontos de grade, etc.
Tudo bem. Não tenho nada a extrapolar, é a interpolação que é necessária. No sentido de que uma previsão sobre tal extrapolação não tem sentido para ser feita posteriormente. É necessário que esta linha seja tão forte quanto possível, de um lado ao outro, como sua linha azul. E quero poder obter uma solução sobre os novos pontos, sim (sem recalcular com base na fórmula existente).
Por isso, basta perguntar o que é melhor usar - polinômios ou estrias ou alguma subespécie. E talvez o 10º grau também fosse legal.
Interpolação exata? Você tem certeza? Não é uma aproximação? E não é redesenhável?
Você não vai interpolar cada carrapato.
Se você precisar de interpolação em nós intermediários (nós ZigZag, por exemplo) sem redesenhar, então todo o ponto é onde estará o próximo nó.
Você só pode criar um ZigZag transparente não redesenhável se você tiver uma máquina do tempo. Não há como determinar, sem uma máquina do tempo, que a barra atual é um extremo.
Há alguém no fórum periodicamente a quem eu chamo de "desenhista de rabo".
O objetivo é o rabo de cavalo.
É um clássico deste gênero - deslocar o SMA para a esquerda por meio período e terminar de desenhar esses meios períodos como se fosse por acidente com um polinômio de algum grau. Por exemplohttps://www.mql5.com/ru/forum/224374. Você provavelmente já o viu.
Você pode fazer uma interpolação muito agradável ao longo de ziguezague extrema com estrias, mas você precisa entender claramente que entre os últimos dois ou três nós haverá um redesenho. Não há como sem ele!
Se não for redesenhado, não é interpolação, mas o que eu chamo de traço da linha de aproximação (não interpolação!).
Além dos polinômios, não vejo nada compreensível até agora.
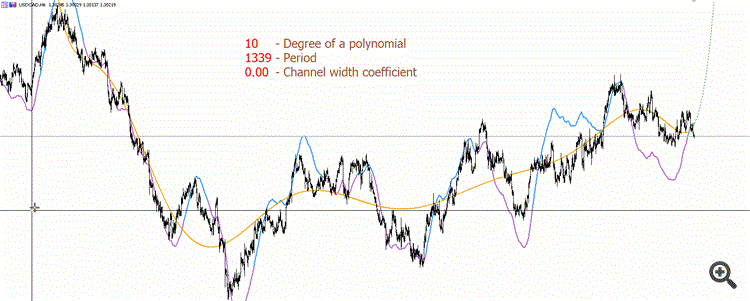
Aqui está um gif especialmente gravado para demonstrar um exemplo de polinômio de maior grau (10), a fim de entender o quanto é menos "bonito" do que eu gostaria :))
A linha roxa e azul não é redesenhável. Roxo é o polinômio "olhando para baixo", azul é o polinômio "olhando para cima".
E não há precisão suficiente para calcular polinômios de alto grau. Teremos que usar bibliotecas especiais usando tipos de maior precisão. O fato de o "traçador" começar a "pular" em pequenos períodos no gif - esta é a razão pela qual o dobro carece de precisão.
Mas pessoalmente não vejo a aplicação prática de polinômios de grau superior a 5.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Preciso interpolar uma função com ajustes arbitrários, por isso escolhi estrias.
Entendo corretamente que obterei interpolantes diferentes pelo número de pontos de nodo, o que mais posso variar?
E a segunda pergunta, o que é melhor escolher para a interpolação a partir da lista, se eu preciso apenas construir muitas interpolações diferentes da série original (a variação é importante)